Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания. Источники грамонических колебаний. Способы представления гармонических колебаний. Векторные диаграммы.Содержание книги
Поиск на нашем сайте
Переменный ток, напряжение. Периодические токи и напряжения. Мгновенные значения тока, напряжения и э.д.с. Наибольшее распространение в электрических цепях получили синусоидальные или гармонические токи и напряжения. Ток, изменяющийся по закону синуса называется синусоидальным или гармоническим. Мгновенное значение синусоидального тока, напряжения, э.д.с.:
Период T, частота f связаны соотношением: Важными параметрами синусоидальных колебаний являются действующее и среднее значения. Действующим значением тока I называется среднеквадратичное значение электрического тока за период:
Среднее значение гармонического тока за период равно нулю, поэтому пользуются понятием среднего полупериодного значения, соответствующего только положительной полуволне:
Генератор переменной э.д.с. Устройство и принцип действия. Синусоидальные колебания (токи, напряжения, э.д.с.) можно представить различными способами: функциями времени в Расчет электрических цепей с синусоидальными источниками энергии облегчается, если синусоидально изменяющиеся токи, напряжения, э.д.с. изображать векторами или комплексными числами. Эти представления лежат в основе символического метода расчета электрических цепей – метода комплексных амплитуд. Векторное представление синусоидальных функций основано на том, что каждой синусоидальной функции в соответствии ставится вращающийся вектор на комплексной плоскости. Этот вектор на комплексной плоскости является геометрическим изображением комплексного числа, поэтому синусоидальным функциям соответствуют комплексные числа. Мгновенному значению напряжения В начальный момент времени
Из приведенных выражений следует, что напряжение 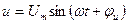 можно рассматривать как проекцию вращающегося вектора можно рассматривать как проекцию вращающегося вектора 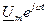 на ось мнимых чисел: на ось мнимых чисел:  , а напряжение , а напряжение 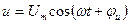 как проекцию вектора как проекцию вектора 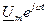 на ось вещественных чисел: на ось вещественных чисел:
Вместо комплексных амплитуд часто рассматривают комплексные действующие величины:
Переход от синусоидальных функций к комплексным действующим значениям позволяет упростить действия с синусоидальными функциями: сложение и вычитание, дифференцирование и интегрирование:
Используя формулу Эйлера, показательная форма преобразована в алгебраическую форму комплекса напряжения. Переход из алгебраической формы в показательную форму:
Умножение вектора на j и на –j.Пустьимеетсявектор Сложение гармонических функций. При анализе электрических цепей синусоидального тока приходится сталкиваться с суммированием синусоидальных функций времени с одинаковой частотой, но с различными начальными фазами. Непосредственное сложение в t- области связано с большими трудностями тригонометрического характера. Значительно проще задача решается графически при помощи векторной диаграммы или аналитически - путем суммирования комплексных чисел. Основная литература: 1[66 – 71]; 2[61 - 68]. Дополнительная литература: 9 [106 - 115]. Контрольные вопросы:
1. Параметры синусоидального напряжения и тока? 2. Каковы преимущества синусоидального напряжения? 3. Максимальное, действующее, среднее значение синусоидального напряжения, тока? 4. Как можно представить синусоидальную функцию времени? 5. Показательная форма комплексной амплитуды напряжения. 6. Алгебраическая форма комплексной амплитуды напряжения. 7. Найти графически сумму двух синусоидальных токов. Определить действующее значение и начальную фазу. Лекция 5. Гармонические колебания в цепи с резистивным, индуктивным и емкостным элементом. Символический метод. Анализ разветвленных цепей при гармонических воздействиях. Пассивный двухполюсник. Схемы замещения духполюсника при заданной частоте. Активная, реактивная и полная мощности. Резистивный элемент в цепи синусоидального тока. Активная мощность.
Пусть к резистивному элементу приложено синусоидальное напряжение Ток в цепи определяется законом Ома:
Амплитуда тока определяется законом Ома, сдвиг фаз равен нулю, т.е. ток и напряжение на резистивном элементе совпадают по фазе. Мгновенная мощность в резистивном элементе:
Мгновенная мощность пульсирует от нулевого значения до максимума с двойной частотой и принимает только положительные значения. Среднее значение мощности за период называется активной мощностью:
В комплексной форме:
Пусть через индуктивный элемент протекает синусоидальный ток:
Мгновенная мощность:
Схема замещения реальной катушки представляет собой последовательное соединение активного сопротивления и индуктивности катушки. Схема замещения индуктивной катушки. Комплексное сопротивление. Векторная диаграмма. Активная и реактивная мощности реальной катушки индуктивности. Идеализированный емкостной элемент в цепи синусоидального тока. Реактивная мощность. Пусть к обкладкам конденсатора приложено синусоидальное напряжение тогда ток определяется Активная мощность: Реактивная мощность: В комплексной форме:
где
Основная литература: 1[71 - 73], 2[84 - 85]. Контрольные вопросы: 1. Соотношения между амплитудами и начальными фазами синусоидального тока и напряжения на зажимах индуктивного элемента. 2. Реактивная мощность индуктивного элемента.
3. Комплексное сопротивление индуктивного элемента. 4. Схема замещения реальной катушки индуктивного элемента. 5. Комплексное сопротивление емкостного элемента. 6. Векторная диаграмма емкостного элемента.
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.224 (0.009 с.) |

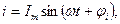
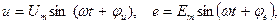 где:
где: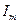 ,,
,, 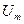 ,
, 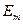 максимальное значение или амплитуда тока, напряжения, э.д.с.;
максимальное значение или амплитуда тока, напряжения, э.д.с.;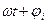
 ,
, 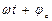 - фаза тока, напряжения, э.д.с.;
- фаза тока, напряжения, э.д.с.;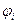 ,
, 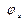 ,
, 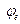 - начальная фаза тока, напряжения. э.д.с.;
- начальная фаза тока, напряжения. э.д.с.;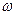 - угловая частота.
- угловая частота.
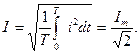 Аналогично для напряжения и э.д.с.:
Аналогично для напряжения и э.д.с.: 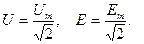
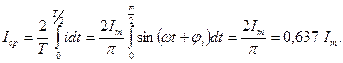
 -области (временные диаграммы), векторами, комплексными числами.
-области (временные диаграммы), векторами, комплексными числами.
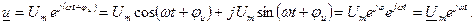
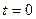 , получается начальное положение вектора, который образует с вещественной осью угол
, получается начальное положение вектора, который образует с вещественной осью угол 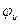 . Такой вектор обозначается
. Такой вектор обозначается  и называется комплексной амплитудой. Модулем комплексной амплитуды является вещественная амплитуда синусоидального напряжения, а аргументом – начальная фаза, т.е. комплексная амплитуда включает оба параметра синусоиды: амплитуду и фазу. Это очень важное свойство комплексной амплитуды. Вектор
и называется комплексной амплитудой. Модулем комплексной амплитуды является вещественная амплитуда синусоидального напряжения, а аргументом – начальная фаза, т.е. комплексная амплитуда включает оба параметра синусоиды: амплитуду и фазу. Это очень важное свойство комплексной амплитуды. Вектор 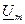 неподвижен. Множитель
неподвижен. Множитель 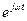 является оператором вращения.
является оператором вращения. 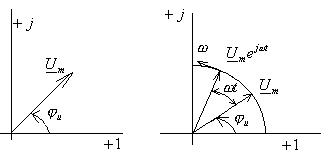
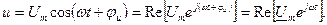
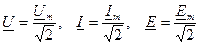 .
. - дифференцирование соответствует умножению на
- дифференцирование соответствует умножению на  , а операция интегрирования соответствует делению на
, а операция интегрирования соответствует делению на 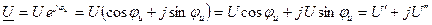 ,
,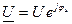 показательная форма комплекса напряжения,
показательная форма комплекса напряжения,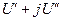 - алгебраическая форма комплекса напряжения.
- алгебраическая форма комплекса напряжения.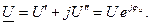
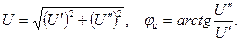
 . Умножение его на jдает вектор, по модулю равный U, но повернутый по отношению к исходному вектору на угол
. Умножение его на jдает вектор, по модулю равный U, но повернутый по отношению к исходному вектору на угол 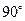 в сторону опережения (против часовой стрелки). Умножение вектора
в сторону опережения (против часовой стрелки). Умножение вектора 
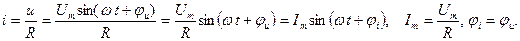

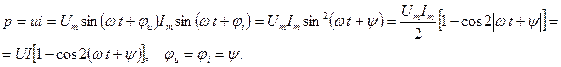
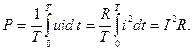
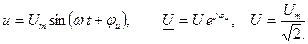

 ,тогда напряжение:
,тогда напряжение: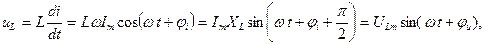
 - амплитуда напряжения,
- амплитуда напряжения,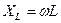 -индуктивное сопротивление,
-индуктивное сопротивление, - индуктивная проводимость,
- индуктивная проводимость, - начальная фаза напряжения. Из этих выражений видно, что амплитуда напряжения и тока связаны законом Ома. На индуктивном элементе напряжение по фазе опережает ток на угол
- начальная фаза напряжения. Из этих выражений видно, что амплитуда напряжения и тока связаны законом Ома. На индуктивном элементе напряжение по фазе опережает ток на угол 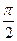 или 90 градусов. Сдвиг фаз между напряжением и током
или 90 градусов. Сдвиг фаз между напряжением и током 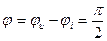 т.е., ток отстает по фазе от напряжения на угол
т.е., ток отстает по фазе от напряжения на угол 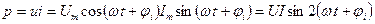 , изменяется по синусоидальному закону с двойной частотой. Среднее значение мощности за период равно нулю:
, изменяется по синусоидальному закону с двойной частотой. Среднее значение мощности за период равно нулю: 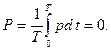 Реактивная мощность
Реактивная мощность  индуктивности. Измеряется вольт ампер реактивных
индуктивности. Измеряется вольт ампер реактивных  .
. Комплексной форме:
Комплексной форме:
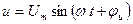 ,
,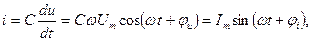 где
где 
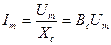 - амплитуда тока,
- амплитуда тока,  - емкостное сопротивление,
- емкостное сопротивление, 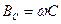 - емкостная проводимость,
- емкостная проводимость, 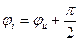 - начальная фаза тока,
- начальная фаза тока,  - сдвиг фаз между напряжением и током. Ток на конденсаторе опережает по фазе напряжение на угол
- сдвиг фаз между напряжением и током. Ток на конденсаторе опережает по фазе напряжение на угол 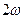 и амплитудой
и амплитудой 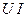 :
:  .
.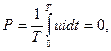

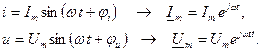
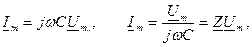
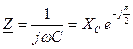 - комплексное сопротивление емкостного элемента,
- комплексное сопротивление емкостного элемента, - комплексная проводимость емкостного элемента,
- комплексная проводимость емкостного элемента,  - емкостная проводимость
- емкостная проводимость