
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Комплексное сопротивление. Комплексная проводимость. Пассивный двухполюсник. Схемы замещения. Законы Ома и Кирхгофа в комплексной форме.Содержание книги
Поиск на нашем сайте
Комплексное сопротивление равно отношению комплекса напряжения к комплексу тока или комплексного максимального значения напряжения к комплексному максимальному значению тока
где: Z – модуль комплексного сопротивления называется полным сопротивлением,
Графически выражение Комплексная проводимость. Величину, обратную комплексному сопротивлению
где: Y -модуль комплексной проводимости называется полной проводимостью,
Если известна комплексная проводимость, то можно получить комплексное сопротивление. Пассивный двухполюсник. Схемы замещения. По известному входному комплексному сопротивлению двухполюсника можно получить последовательную схему замещения двухполюсника, состоящую из последовательного соединения активного сопротивления и реактивного сопротивления. В зависимости от знака реактивного сопротивления, его можно рассматривать как индуктивное или как емкостное. Напряжение
где
Из треугольника напряжений следует Входной проводимости
где Составляющие Треугольник образованный Закон Ома и Кирхгофа в комплексной форме. Закон Ома: Первый закон Кирхгофа: алгебраическая сумма комплексных токов ветвей, соединенных в узел, равна нулю: Второй закон Кирхгофа: алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контура равна нулю. Его можно сформулировать другим образом: алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контура равна алгебраической сумме комплексных э.д.с. всех источников напряжения в этом контуре: Законы Кирхгофа можно записать и для мгновенных значений. Алгебраическая сумма мгновенных значений токов в ветвях, соединенных в узле равна нулю: Алгебраическая сумма мгновенных напряжений на всех элементах любого замкнутого контура схемы равна нулю: Основная литература: 1[71 -73, 76 – 79)]; 2 [68 – 75, 77-80, 84 - 85]. Дополнительная литература: 9 [123 -126, 128 -132]. Контрольные вопросы: 1. Написать закон Ома и Кирхгофа в комплексной форме. 2. Комплексная, полная, реактивная проводимости. 3. Треугольник проводимости. 4. Как перейти от комплексных сопротивлений к комплексным проводимостям и обратно? 5. Соотношения между амплитудами и начальными фазами синусоидального тока и напряжения на резистивном элементе. 6. Чему равен угол сдвига фаз между напряжением и током на резистивном элементе?
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.144.139 (0.005 с.) |



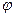 - аргумент комплексного сопротивления называется сдвиг фаз между напряжением и током,
- аргумент комплексного сопротивления называется сдвиг фаз между напряжением и током,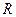 - вещественная часть комплексного сопротивления называется активным сопротивлением,
- вещественная часть комплексного сопротивления называется активным сопротивлением,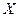 - мнимая часть комплексного сопротивления называется реактивным сопротивлением.
- мнимая часть комплексного сопротивления называется реактивным сопротивлением. можно представить треугольником сопротивлений. Комплексное сопротивление идеальных двухполюсников: для сопротивления R
можно представить треугольником сопротивлений. Комплексное сопротивление идеальных двухполюсников: для сопротивления R  (активное), для индуктивности L - комплексное сопротивление
(активное), для индуктивности L - комплексное сопротивление  , где
, где  -реактивное сопротивление индуктивности; комплексное сопротивление емкостного элемента
-реактивное сопротивление индуктивности; комплексное сопротивление емкостного элемента  , где
, где  -реактивное сопротивление емкостного элемента.
-реактивное сопротивление емкостного элемента. называют комплексной проводимостью:
называют комплексной проводимостью:
 - активная проводимость,
- активная проводимость,  – реактивная проводимость. Графически данное выражение
– реактивная проводимость. Графически данное выражение  можно представить в виде треугольника проводимости. Комплексная проводимость этих же элементов:
можно представить в виде треугольника проводимости. Комплексная проводимость этих же элементов:  Если известно комплексное сопротивление, то можно найти проводимость:
Если известно комплексное сопротивление, то можно найти проводимость:
 можно разложить на две составляющие:
можно разложить на две составляющие:
 - составляющая, совпадающая по фазе с током, называется активной составляющей напряжения,
- составляющая, совпадающая по фазе с током, называется активной составляющей напряжения,  - составляющая, сдвинутая по фазе относительно тока на угол
- составляющая, сдвинутая по фазе относительно тока на угол 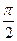 , называется реактивной составляющей напряжения. Составляющие
, называется реактивной составляющей напряжения. Составляющие 

 соответствует параллельная схема замещения из активной проводимости и реактивной проводимости. Реактивная проводимость в зависимости от знака либо индуктивная, либо емкостная. Ток на входе может быть представлен:
соответствует параллельная схема замещения из активной проводимости и реактивной проводимости. Реактивная проводимость в зависимости от знака либо индуктивная, либо емкостная. Ток на входе может быть представлен: ,
, - составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока,
- составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока,  составляющая, сдвинутая по фазе относительно напряжения на угол
составляющая, сдвинутая по фазе относительно напряжения на угол  называется треугольником токов.
называется треугольником токов.



 , или алгебраическая сумма мгновенных э.д.с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура.
, или алгебраическая сумма мгновенных э.д.с. всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура.


