
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод основного уравнения ОТ для ансамбля простых явлений.Содержание книги
Поиск на нашем сайте
Мы теперь располагаем экстенсорами Ε (см. соотношение (27)), играющими роль аргумента N1 в уравнении (14). Этого вполне достаточно, чтобы написать основное уравнение ОТ применительно к ансамблю простых явлений и определить все остальные величины, входящие в уравнения (14) и (15), в частности найти неизвестную меру N4, обозначенную нами через U (см. выражение (29)). Благодаря этому мы, наконец, сформулируем наиболее общие, универсальные и достоверные количественные принципы, или начала, которые обнаруживаются на первом - начальном - этапе эволюции вещества и его поведения. Таким образом, будет замкнута цепочка дедуктивных рассуждений (2) и завершено построение обещанного выше общего метода дедукции, который берет свое начало от весьма общих философских концепций и затем в ходе рассуждений опускается до уровня числового выражения свойств конкретных явлений. Мы убедимся, что основное уравнение (14), написанное для ансамбля простых явлений, представляет собой не что иное, как первое начало ОТ. Дальнейшая расшифровка характеристик и связей, содержащихся в первом начале, приведет к формулировке остальных шести начал. На этом завершится построение общего метода дедукции. Разработанный таким способом аппарат ОТ будет использован для изучения отдельных явлений эволюционного ряда (24). Основное уравнение ОТ применительно к ансамблю простых явлений получается из соотношений (14), (27) и (29). Имеем U = F(E1; E2;...; Ei) (30) Мера количества поведения вещества ансамбля U есть однозначная функция всех мер Ε количества вещества; число веществ различного сорта, из которых построен ансамбль, равно l. Как уже отмечалось, нам пока известно семь таких разнородных веществ. Вида функции F мы не знаем. Абсолютные значения многих характеристик явления обычно найти труднее, чем изменения этих характеристик. Поэтому уравнение (30) надо преобразовать таким образом, чтобы в него входили только изменения (разности) соответствующих величин. Для этого достаточно продифференцировать выражение (30). В соответствии с хорошо известными правилами дифференцирования функции нескольких переменных полное изменение меры U (полный дифференциал dU)определяется в виде суммы произведений скорости приращения функции с аргументом на приращение этого аргумента, то есть dU = или dU = где Pk = (¶U/¶Ek)Ein (33) dQk = PkdEk Дж (34)
Индекс Еin стоящий внизу скобки, говорит о том, что при дифференцировании все остальные экстенсоры, кроме данного, k -того,остаются постоянными (инвариантными). Равенство (31) в аналитической форме выражает общее дифференциальное уравнение первого начала ОТ. Определенные совокупности найденных величин обозначены буквами Ρ и Q; смысл этих символов, как и самого уравнения, включая его размерность, выясняется ниже. Для большей наглядности свои рассуждения мы нередко будем иллюстрировать самыми простыми примерами, в которых ансамбль состоит всего из двух разнородных веществ, определяемых двумя экстенсорами (l = 2). При этом основные идеи ОТ сохраняют свою силу, но дифференциальные уравнения оказываются наименее громоздкими. Итак, в частном случае, когда 1 = 2, уравнения (31)-(34) приобретают вид dU = P1dE1 + P2dE2 Дж, (35) или dU = dQ1 + dQ2 Дж, (36) где P1 = (¶U/¶E1)E2; P2 = (¶U/¶E2)E1 (37) dQ1 = P1dE1; dQ2 = P2dE2 (38) Индекс Е2 внизу первой скобки означает, что при дифференцировании меры U по Е1 постоянной считается величина Е2;индекс Е1 у второй скобки говорит о постоянстве величины Е1. В еще более простом гипотетическом частном случае, если ансамбль содержит только одно вещество (l = 1), то основное дифференциальное уравнение ОТ записывается следующим образом: dU = PdE Дж (39) или dU = dQ Дж (40) где P = dU/dE (41) dQ = PdE (42) Мы добились того, что в найденном дифференциальном уравнении первого порядка (31) отсутствует неизвестная функция F. Кроме того, главные количественные меры входят в это уравнение в виде интересующих нас изменений (разностей). Теперь нам предстоит внимательно рассмотреть физический смысл самого уравнения и всех содержащихся в нем характеристик [ТРП, стр.91-93].
Виды работы.
В уравнении (31) хорошо нам известными характеристиками являются только экстенсоры Е. Но для одного частного случая - силового взаимодействия - мы знаем также фактор интенсивности, или интенсиал, каковым служит сила Рх. В этом частном случае произведение интенсиала на изменение экстенсора dEx (перемещение dx)равно работе dQx,которая измеряется в джоулях (см. формулу (28)). Следовательно, все остальные слагаемые правой части уравнения (31) также должны представлять собой работы, измеряемые в джоулях. Этот факт отражен в уравнении, записанном в форме (32). Интересная особенность вопроса заключается в том, что каждая из работ сопряжена со своим специфическим экстенсором, имеющим особую размерность. В любом таком конкретном случае экстенсор «окрашивает» работу в свой специфический «цвет». Например, приходится различать работы кинетическую, механическую, электрическую и т.д. В этом смысле обсуждаемые работы можно рассматривать как специфические. Вместе с тем любая данная работа в целом есть универсальная мера силового взаимодействия данного вещества с ансамблем, ибо измеряется в одних и тех же единицах - джоулях - и состоит из универсальной меры интенсивности силового взаимодействия, или силы, измеряемой в ньютонах, и универсальной меры экстенсивности силового взаимодействия, или перемещения, измеряемого в метрах. Это дает основание считать работу некоей универсальной мерой количества воздействия на ансамбль. В термодинамике величину dQ часто именуют обобщенной работой. Здесь мы сталкиваемся с удивительно органичным сочетанием универсального (обобщенного) и специфического (конкретного), одновременно присутствующих в одном из основных понятий теории. Это хорошо перекликается с высказанной ранее идеей о целесообразности и плодотворности синтеза обобщенного и конкретного подходов. Работа совершается в процессе подвода или отвода от ансамбля определенного количества вещества, мерой которого служит экстенсор dE. Этот подвод или отвод можно рассматривать как некое специфическое воздействие на ансамбль веществом определенного сорта. Следовательно, специфической мерой количества воздействия на ансамбль является изменение экстенсора dE. Таким образом, изменение количества вещества ансамбля, определяемое экстенсором dE, одновременно сопровождается двумя видами воздействий - специфическим и универсальным. Мерой количества специфического воздействия служит экстенсор dE,а мерой количества универсального - работа dQ. Нетрудно сообразить, что специфическая мера количества воздействия на ансамбль, или величина dE, одновременно является специфической мерой экстенсивности силового взаимодействия между ансамблем и квантами подводимого или отводимого вещества определенного сорта. Здесь также сталкиваются между собой две противоположные сущности - конкретная и обобщенная, ибо специфическая особенность вещества накладывается на универсальное свойство перемещения: ведь обе величины - dE и dx, - будучи аргументами в основном уравнении ОТ, с равным успехом определяют одну и ту же обобщенную работу dQ (см. формулы (28) и (34)). Хотя работы, определяемые выражениями (28) и (34), друг другу равны, у них имеется и существенное различие. Разумеется, оно касается только правых частей уравнений, ибо левые тождественны между собой. Имеющееся различие заключается в том, что работа (28) выражена через предельно универсальные характеристики процесса - силу и перемещение, а работа (34) - через специфические характеристики того же процесса. О специфичности экстенсора говорилось уже достаточно, теперь предстоит заняться мерой Р [ТРП, стр.93-95].
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.15 (0.006 с.) |

 Дж, (31)
Дж, (31)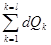 Дж, (32)
Дж, (32)


