Закон отношения проводимостей.

 

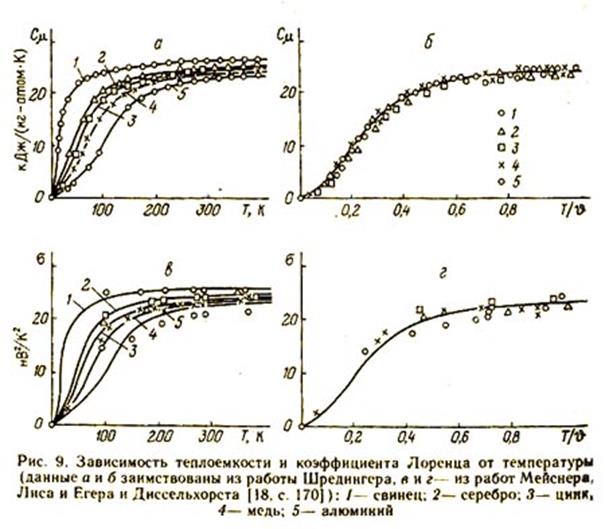
Воспользуемся теперь началами, определяющими явления переноса, и выведем еще два новых закона, из которых выте­кают многие известные законы физики и химии; для простоты рассмотрим две степени свободы. Первый закон - отношения проводимостей - получается из соотношений (106), (112), (113), (117), (118), (122), (123), (127), (128). При n = 2имеем [16, с.24; 17, с.65; 18, с.167; 21, с.185]

a₁₁/a₂₂ = b₁₁/b₂₂ = L₁₁/L₂₂ = M₁₁/M₂₂ = s = K_P11/K_P22 = A_P22/A_P11; (298)

a₁₂/a₁₁ = b₁₂/b₁₁ = L₁₂/L₁₁ = M₁₂/M₁₁ = s₁₂₁₁ = K_P12/K_P11 = A_P11/A_P12. (297)

Закон отношения проводимостей формулируется следующим образом: отношение проводимостей s или s₁₂₁₁ для любой пары степеней свободы системы равно отношению сопряженных с ними емкостей.

Из законов отношения проводимостей и тождественности в качестве частного случая вытекает известный опытный закон Видемана-Франца (1853 г.) с поправкой Лоренца (1872 г.). Применительно к термоэлектрической системе, если в формуле (296) вермопроводность L_Q и вермоемкость К_Q выразить через теплопроводность L_Q и теплоемкость С, а электроемкость К_Y - через аналог газовой постоянной R_Y из соответствующего уравнения состояния для идеальной термоэлектрической систе­мы, то получится выражение [18, с.168; 21, с.186]

L_Q/ L_Y = sТ = R_YиС_mТ (298)

где

s = R_YиС_m (299)

Индексом μ отмечены мольные значения величин.

Это и есть искомое теоретическое уравнение. Совместно с приближенным законом тождественности, утверждающим одинаковость мольных емкостей, оно говорит о том, что отноше­ние теплопроводности к электропроводности пропорционально абсолютной температуре Т и приблизительно не зависит от рода металла, коэффициент пропорциональности s именуется коэф­фициентом Лоренца.

Закон Видемана-Франца получается, если правую часть уравнения (298) считать величиной постоянной. Поправку Т ввел Лоренц; он установил, что постоянным является коэффициент s. Однако в действительности, согласно ОТ, коэф­фициент Лоренца s есть величина переменная, определяемая формулой (299); он пропорционален теплоемкости. Для метал­лов в первом приближении можно принять

R_Ym = 10^-12 кг×атом/(Ф×К) (300)

Выводы ОТ хорошо подтверждаются экспериментами, в ко­торых коэффициент Лоренца и теплоемкость определяются независимыми методами. Например, на рис. 9, а приведена опытная зависимость мольной теплоемкости при.постоянном давлении от температуры для различных металлов. Теплоем­кости использованы для определения по формулам (299) и (300) коэффициента Лоренца; эти его значения изображены на рис. 9, е в виде кривых; здесь же точками нанесены опытные коэффициенты Лоренца, найденные как отношение теплопро­водности к электропроводности. Совпадение результатов получается удовлетворительным.

 

Для большей наглядности на рис 9, 6 мольная теплоемкость изображена в функции от относительной температуры Т/J, где J - характеристическая температура, фигурирующая в тео­рии теплоемкости Дебая; при этом, как показал Шредингер, опытные значения теплоемкости для различных металлов груп­пируются вблизи одной кривой. Эта кривая, пересчитанная на коэффициент Лоренца, приведена на рис. 9, г;здесь же в виде точек представлены опытные значения коэффициента Лоренца. Эти точки тоже хорошо группируются вблизи универ­сальной теоретической кривой [17, с.133; 18, с.170].

Предлагаемый способ выражения коэффициента Лоренца через температуру Дебая очень удобен на практике. При определении по формулам (298) и (300) одних величин (неиз­вестных) с помощью других (известных) можно пользоваться обобщенной кривой, приведенной на рис. 9, г,которая дает универсальную зависимость коэффициента s от температуры для различных металлов.

Однако, согласно закону состояния, коэффициент R_Ym, входящий в формулы (298) и (299), постоянен только для идеального ансамбля. У реальных ансамблей он должен быть функцией вермиора и электриора (электрического заряда), а следовательно, температуры и электрического потенциала. В работе [20, с.247] установлена существенная зависимость коэффициента R_Ym от температуры, причем линейная аппрокси­мация этой зависимости дает хорошие по точности результаты. Это позволяет уточнить расчет свойств различных металлов с помощью коэффициента Лоренца.

Коэффициент R_Ym является величиной, обратной электро­емкости К_Ym [20, с.251]. Но всякая емкость обладает свойством аддитивности. Следовательно, на основе аддитивности величи­ны 1/R_Ym можно рассчитывать свойства сплава по известным свойствам отдельных компонентов, входящих в его состав. Соответствующий метод, сопровождаемый многочисленными экспериментальными данными, приводится в монографии [20, с.243].

Опыт показывает, что уравнение (298) может быть исполь­зовано также для определения свойств металлов и сплавов в жидком состоянии. При этом характеристическая температура Дебая уже не играет столь важной роли, как для твердых металлов [20, с.249].

Некоторые из описанных методов пригодны для полупровод­ников. В этом случае наблюдается заметная зависимость коэф­фициента R_Ym не только от температуры, но и от электрического потенциала, что хорошо согласуется с выводами ОТ.

Из сказанного ясно, что ОТ вносит в закон Видемана-Франца и Лоренца серьезные поправки. Во-первых, металлы следует сравнивать при одинаковых не абсолютных (Т), аотносительных (Т/J) температурах. Во-вторых, надо пользоваться не постоянным, а переменным значением коэффициента Лорен­ца. В-третьих, закон Видемана-Франца и Лоренца является в принципе приближенным законом, ибо, согласно ОТ, коэффи­циент Лоренца пропорционален отношению емкостей, а одина­ковость емкостей для различных металлов есть следствие при­ближенного закона тождественности.

Из закона отношения проводимостей вытекают также неко­торые другие известные законы, в частности закон Грюнейзена (1908 г.), согласно которому отношение объемного коэффициен­та теплового расширения к теплоемкости не зависит от темпера­туры [18, с.175]. Кроме того, из закона отношения проводи­мостей могут быть выведены многие новые закономерности для твердых, жидких и газообразных тел и различных степеней свободы системы, охватывающих, например, такие свойства, как диэлектрическая постоянная, магнитная проницаемость, вяз­кость, изотермическая сжимаемость и т.д. [17, 18]. Эти зако­номерности могут быть с успехом применены на практике для определения неизвестных свойств веществ по известным [ТРП, стр.303-306].

 

 

Закон отношения потоков.

 

Вторым упомянутым выше частным законом является закон отношения потоков. Он с количественной стороны характеризует эффект увлечения одних потоков другими. Выводится этот закон в предположении, что все термодинамические силы, кроме дан­ной, равны нулю [18, с.283]. В этих условиях для двух степеней свободы (n = 2), например, из уравнений (116) при Х₂ = 0 получаем

s₁₁₂₁ = (I₁/I₂)_{Х2 =0} = (dE₁/dE₂)_{Х2 =0} = b₁₁/b₂₁ = K_P11/K_P21 (301)

При Х₁ = 0 имеем

s₁₂₂₂ = (I₁/I₂)_{Х1 =0} = (dE₁/dE₂)_{Х1 =0} = b₁₂/b₂₂ = K_P12/K_P22 (302)

Проводимости b в этих равенствах могут быть заменены дру­гими частными проводимостями на основе соотношений (296) и (297) закона отношения проводимостей.

Закон отношения потоков формулируется следующим образом: при наличии нескольких степеней свободы и действии только одной термодинамической силы отношение любых двух потоков или экстенсоров равно отношению сопряженных с ними проводимостей или емкостей.

Закон отношения потоков совместно с приближенным зако­ном тождественности позволяет установить группу ансамблей, в пределах которых соблюдается постоянство (одинаковость) отношения соответствующих потоков. Из этих двух законов вытекают, например, известные эмпирические правило (закон) Трутона [17, с.311; 18, с.337], первый и второй законы Фарадея [18, с.345] и т.д.

Чтобы вывести эти и многие другие законы, надо написать уравнения переноса типа (116) для химической, фазовой, вермической, механической, электрической, диффузионной и неко­торых других степеней свободы. Например, фазовые превраще­ния происходят под действием разности фазовых интенсиалов (фазиалов) δμ_ф. При конечной разности δμ_ф и нулевых значе­ниях разностей всех остальных интенсиалов, включая темпера­туру, из уравнения (302) получается, что отношение удельной мольной теплоты фазового превращения к абсолютной темпера­туре равно отношению соответствующих мольных емкостей. При этом тепловой эффект превращения по существу представляет собой эффект увлечения вермического вещества массой.

Отсюда видно, что закон Трутона, утверждающий, что для одной килограмм-молекулы всех веществ отношение теплоты к температуре испарения или конденсации есть величина посто­янная, соблюдается только в меру постоянства мольных емкос­тей, входящих в правую часть выражения (302). О неточности закона Трутона можно судить по данным, приведенным в работе [18, с.338]. Для процессов плавления и затвердевания закон Трутона выполняется еще хуже, чем для испарения и конденса­ции, так как у жидких и твердых тел емкости сильнее зависят от состава ансамбля, в том числе от его массы, об этом уже говорилось выше.

Таким образом, ОТ позволяет внести в закон Трутона опре­деленные разъяснения, уточнения и ограничения. Во-первых, приходится констатировать, что этот закон в целом правильно отражает общую тенденцию развития процессов испарения и конденсации. Вместе с тем он является в принципе прибли­зительным законом, ибо фактически опирается на приближен­ный закон тождественности. Неточность закона тождествен­ности, а следовательно, и закона Трутона объясняется, как мы уже убедились, наличием всеобщей связи между различными степенями свободы системы. Прежние теории не учитывали этих

связей, поэтому не могли пролить свет на загадочную неточность закона Трутона. Происхождение этой неточности всегда было неясно и вызывало много недоуменных вопросов. Теперь, нако­нец, становятся понятными как физический смысл, так и причи­на приближенности закона Трутона.

Во-вторых, ОТ позволяет внести в закон Трутона весьма существенное ограничение, связанное с действием закона экра­нирования седьмого начала. Это ограничение имеет общий смысл, относится ко всем степеням свободы системы и касается всех случаев определения теплового эффекта различных фазо­вых и химических превращений, реакций, процессов и т.д., поэтому на нем целесообразно остановиться более подробно; суть его заключается в следующем.

Любой реальный процесс протекает под действием опреде­ленной разности интенсиалов. Согласно закону экранирования (222), это связано с выделением или поглощением некоторого количества тепла диссипации (экранирования). Экранирован­ная теплота в принципе неотличима от основной работы перено­симого или увлеченного вермиора. Следовательно, при опреде­лении тепловых эффектов фазовых и химических превращений надо обязательно учитывать степень необратимости реального процесса, то есть количество экранированного в этом процессе тепла.

Например, в случае фазового превращения к увлеченному массой равновесному теплу превращения r_m добавляется (при конденсации и затвердевании) или вычитается (при испарении и плавлении) экранированное тепло в количестве

R_Эm = ТQ_Эm = - δμ_фm_m (303)

где Θ_Эμ - экранированный вермиор, определяемый по формуле (223), m_m - масса одной килограмм-молекулы вещества.

Неучет экранированного тепла r_эm,может привести к сущест­венным ошибкам. Поэтому опыты по определению величины r_m, надо проводить в условиях, близких к равновесным, когда δμ_ф ® 0. В противном случае на величине r_m скажется эффект неравновесности, который обнаружит себя в том, что r_m при кон­денсации и затвердевании будет выше, чем при испарении и плавлении. Равновесное значение r_m, представляющее собой физический коэффициент, заключено между двумя этими значе­ниями. Кстати сказать, отсюда следует, что о степени неравно­весности реального процесса можно судить по отклонению полученной в опыте величины r_m от ее равновесного значения. При этом надо иметь в виду, что на величине r_m может сказаться также неравенство нулю других интенсиалов.

Выведем теперь уравнения первого и второго законов Фарадея, регламентирующих явления электролиза. Для этого в урав­нении переноса типа (116) положим равными нулю все разности интенсиалов, кроме электрического. В результате получается следующее новое теоретическое соотношение [18, с.345; 21, с.190]:

s_mYYY = I_m/I_Y = m/Y = b_mY/b_YY = K_PmY/K_PYY (304)

которое определяет первый закон Фарадея, установленный им экспериментально в 1833-1834 гг.: при электролизе за время t на электродах выделяются количества вещества m, пропорци­ональные количеству электрического заряда Ψ,прошедшего через то же время через электролит. Уравнение (304) закона от­ношения потоков ОТ дает точное значение коэффициента про­порциональности.

При последовательном соединении нескольких электролитов количества выделившихся веществ пропорциональны кило­грамм-эквивалентам этих веществ - таково содержание второ­го закона Фарадея. Под килограмм-эквивалентом понимается отношение m/z, где μ - атомная или молекулярная масса иона, z - его валентность. Иными словами, величина m/z представляет собой массу ансамбля, переносимого (увлечен­ного) единичной порцией (квантом) электрического заряда. Для этого случая из выражения (304) получаем

s_mYYY = m/(zY_F)

где Y_F – электрический заряд, Ф, переносящий один килограмм-эквивалент вещества.

Из двух последних равенств имеем

m = mY/(zY_F) (305)

Первый (304) и второй (305) эмпирические законы Фарадея составляют основу современной электрохимии. Согласно закону отношения потоков, они характеризуют эффект увлечения массы электрическим зарядом. Применить к ним закон тождествен­ности не представляется возможным, так как ионы одинаковой валентности обычно сильно разнятся по массе. Согласно общей теории, равенства (304) и (305) справедливы только в том слу­чае, когда напоры всех интенсиалов, кроме электриала δφ, равны нулю. В противном случае масса может переноситься так­же под действием разностей и других интенсиалов.

С помощью уравнений переноса и закона отношения потоков можно написать большое множество конкретных соотношений типа (301), (302) и (304), выражающих определенные законо­мерности развития различных реальных процессов. Большин­ство этих закономерностей еще нигде не используется и не имеет названий. Но несомненно, что многие из них со временем найдут практическое применение. Характерным примером тому служат известные законы Фарадея и Трутона. Добавление к найденным соотношениям приближенного закона тождествен­ности дает возможность объединить однотипные явления в опре­деленные группы, как это сделано Трутоном и Фарадеем.

В настоящей главе и ранее неоднократно упоминаются так называемые физические коэффициенты. Согласно ОТ, физичес­кими коэффициентами служат коэффициенты при экстенсорах и интенсиалах в уравнениях состояния и переноса, а также в уравнениях более высоких порядков. Например, к ним отно­сятся коэффициенты состояния, емкости и проводимости и т.п., а также комбинации из указанных характеристик типа s, R, r, Y_F и т.д. Важно подчеркнуть, что все они суть функции экстенсоров и, следовательно, в принципе являются величинами переменными. В определенных условиях их можно условно, с большим или меньшим приближением к действительности, рассматривать как величины постоянные; часто это приводит к существенному упрощению задачи, например, в случае идеаль­ного тела (см. параграф 7 гл. X). Хорошие результаты при этом дают осредненные значения коэффициентов в соответст­вующем диапазоне изменения параметров.

Физическими коэффициентами не являются главные коли­чественные характеристики ансамбля - экстенсоры, а также энергия, служащая производным свойством первого порядка, интенсиалы, служащие производными свойствами второго порядка, работа и некоторые другие величины. Вместе с тем экстенсоры содержат в себе характеристики, которые по спра­ведливости могут быть названы фундаментальными, или абсо­лютными,или мировыми физическими постоянными (константа­ми). Таковыми служат минимальные порции (кванты) различ­ных простых веществ, например электрического (заряд электро­на, или электриант е),вермического (вермиант t), вибрацион­ного (постоянная Планка h) и т.д. Не исключено, что и эти константы способны претерпевать какие-то изменения со време­нем [18, с.196; 21, с.242]. Все остальные коэффициенты не являются константами в истинном смысле этого слова [ТРП, стр.306-310].

 

 

Теорема интенсиалов.

 

Для завершения краткой иллюстрации различных способов применения начал рассмотрим одну весьма любопытную теоре­му, которая характеризует определенные тенденции развития самопроизвольных природных процессов. Теорема гласит, что в изолированной неравновесной системе среднее значение лю­бого данного интенсиала способно и вынуждено самопроиз­вольно изменяться за счет других интенсиалов; количествен­ная сторона и направление этого изменения определяются конкретными свойствами системы. Докажем эту теорему с по­мощью семи начал ОТ [20, с.240; 21, с.176].

Дана реальная изолированная неравновесная система, об­ладающая n степенями свободы и удовлетворяющая условию (298). В объеме такой системы происходит непрерывное само­произвольное перераспределение всех n веществ и постепенное выравнивание всех n интенсиалов. Этот процесс сопровождает­ся следующими эффектами.

Согласно уравнению (31) первого начала ОТ, суммарная энергия системы остается неизменной, то есть

dU = 0; U = const.

Согласно уравнению (50) второго начала ОТ, общее коли­чество любого i -того вещества системы сохраняется постоян­ным, то есть

dE_i = 0; Ε_i = const.

Перераспределение веществ в системе подчиняется пятому и шестому началам, а изменение состояния - третьему и чет­вертому. Система является реальной; это значит, что в общем случае в ней все коэффициенты состояния суть величины переменные. Отсюда прямо следует, что выравнивание интен­сиалов неизбежно сопровождается изменением их средних значений. Средние значения могли бы оставаться постоянными только в том случае, если бы система была идеальной, то есть обладала бы постоянными значениями коэффициентов состоя­ния (емкостей).

Весьма существенно, что изменениям подвергаются сред­ние значения всех интенсиалов. Это объясняется всеобщей связью явлений и находит свое выражение в неравенстве нулю перекрестных коэффициентов состояния. В результате каждый данный интенсиал испытывает влияние со стороны всех n перераспределяющихся веществ одновременно.

Не менее существенно и то обстоятельство, что изменение средних значений любого данного интенсиала может происхо­дить только за счет других, ибо подчиняется законам сохране­ния энергии и экстенсора. Благодаря этому возрастание каждо­го данного интенсиала по необходимости влечет за собой уменьшение остальных и наоборот. Теорема доказана.

Эффект самопроизвольного изменения интенсиалов изоли­рованной неравновесной системы усиливается благодаря дейст­вию седьмого начала ОТ, особенно его закона экранирования. Выделяющееся экранированное вермическое вещество поступа­ет в общий фонд свободных аргументов уравнения состояния и через последнее изменяет все остальные интенсиалы. На сред­ние значения интенсиалов могут повлиять также другие содер­жащиеся в системе и высвобождающиеся экранированные ве­щества.

Как видим, даже простые процессы перераспределения веществ способны вызвать изменение средних значений интен­сиалов. Возможности изменений заметно расширяются при на­личии в системе более сложных естественных или искусственно воспроизводимых процессов, например круговых.

Весьма важно, что теорема интенсиалов справедлива для любых степеней свободы системы - хрональной, метрической, кинетической, ротационной, вибрационной, вермической, электрической и т.д. Особый интерес представляет кинетичес­кая степень, у которой интенсиалом служит скорость в квадрате. Это значит, что теорема утверждает способность и необходи­мость изменения скорости изолированной системы за счет из­менения других ее интенсиалов, то есть утверждает прин­ципиальную осуществимость безопорных движителей (БМ) [20, с.242; 21, с.178]. Соответствующий пример изменения скорости естественного тела, каковым является планета Земля, обсуждается в работе [21, с.179]. Теория и практика осуществ­ления искусственных БМ рассматриваются в гл. XXI и XXII.

На этом можно закончить краткое изложение различных характерных способов применения начал. Приведенные приме­ры хорошо иллюстрируют возможности теории. Теперь можно приступить к более подробному изучению свойств всевозмож­ных явлений, находящихся на различных количественных и ка­чественных уровнях мироздания, а также к более детальному анализу различных известных законов, теорий и научных дисциплин. Начнем с повторного рассмотрения наипростейшего макроявления, или парена, но уже с привлечением всего аппа­рата ОТ [ТРП, стр.310-312].