
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет цилиндрической прямозубой передачи на контактную прочностьСодержание книги
Поиск на нашем сайте
3.43. Расчет прочности контактирующих поверхностей зубьев основан на ограничении наибольших нормальных напряжений. При выводе формул приняты следующие допущения: зубья рассматривают как два находящихся в контакте цилиндра с параллельными образующими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно распределенной по длине зуба; контактирующие профили предполагают неразделенными масляной пленкой. На основании этих допущений к расчету зубчатых колес можно применить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:
где q — расчетная удельная нормальная нагрузка; Епр — приведенный модуль упругости материалов зубьев; ρпр — приведенный радиус кривизны профилей зубьев шестерни и колеса; ц — коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки q = Fт /l∑, (3.17) где Fn = F,/cosaω — нормальная сила, действующая на зуб (см. рис. 3.35); Ft — окружная сила; l∑ = bωKεεa — суммарная длина контактной линии (для прямозубых передач 1∑ = Ьω — ширина венца, так как Kεεa ≈1,0; здесь Кε = 0,95 — коэффициент, учитывающий непостоянство суммарной длины контактной линии); εa — коэффициент перекрытия. Для учета неравномерности распределения нагрузки по длине контактных линий, а также для учета динамических нагрузок вследствие погрешности изготовления и деформации деталей передачи вводят коэффициент нагрузки К= КНβКНV (см. табл. 3.4—3.5). Отсюда
Приведенный модуль упругости Епр = 2Е1Е2/(Е1 + Е2), где Ех и Е2 — модули упругости материалов шестерни и колеса. Зубья рассматриваются как цилиндры длиной Ьа (ширина зубчатого колеса) и радиусов ρ1 и ρ2, где
Приведенный радиус кривизны зубьев в полюсе
Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внутреннего зацепления. Подставляя значения ρпр и q в формулу (3.17), после преобразований получим
Обозначим в формуле (3.19) выражение
материалов сопряженных колес (ZM = 275 МПа1/2 — для стальных колес);
Получим расчетную формулу, рекомендуемую для проверочного расчета:
После подстановки значений Ft= 2T2/d1u; d1 = 2aω/(u
Значение ΨЬа определяют по формуле ΨЬа = 2Ψba/(u+ 1) (Ψbd — см. табл. 3.7). Расшифруйте формулу (3.21) и подставьте единицы измерения параметров, входящих в эту формулу.
3.44. После некоторых преобразований формулы (3.21) получим формулу проектировочного расчета для определения межосевого расстояния прямозубых зубчатых передач:
Обозначим Ка (для прямозубых передач при KHv = 1,25, Ка = 49,5 МПа1/3). Тогда формула проектного расчета для определения межосевого расстояния закрытых цилиндрических передач
Проанализируйте формулы (3.17), (3.21), (3.22). В каких зубьях {шестерни или колеса) возникает большее нормальное контактное напряжение?
3.45. Допускаемые контактные напряжения (МПа) при расчете рабочих поверхностей на усталостное выкрашивание рассчитываются по формуле [σ] н = (σHlimb /SH)ZRKHL, где σHlimb — предел выносливости рабочих поверхностей зубьев (табл. 3.9). соответствующий базовому числу циклов перемены напряжений NHlim, МПа (база испытаний NH0 определяется по табл. 3.10); SH — коэффициент безопасности {SH= 1,1 при нормализации, улучшении или объемной закалке; при поверхностной закалке и цементации SH=1,2); ZR — коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев (ZR = 1 ÷ 0,9); KHL — коэффициент долговечности, который учитывает влияние срока службы, режима нагрузки передачи и возможность повышения допускаемых напряжений для кратковременно работающих передач.
Таблица 3.9. Пределы контактной выносливости σHlimb
При постоянной нагрузке КHL = NH= 573ωct∑) — циклическая долговечность (см. шаг 3.40). При переменной нагрузке расчетная циклическая долговечность определяется по формуле: NHE = 60 · п · с · t∑ · KHE, где КНЕ — коэффициент приведения переменного режима нагружения к постоянному эквивалентному
В расчетные формулы (3.21) и (3.22) входит меньшее из допускаемых напряжений, установленных для шестерни и колеса. Так как материал колеса имеет обычно меньшую твердость, чем материал шестерни, то в большинстве случаев [σ]н для колеса меньше. В табл. 3.9 даны значения предела выносливости σHlimb (база испытаний) для различных материалов зубчатых колес. По данным примера (шаг 3.40) определить допускаемые контактные напряжения для шестерни колеса прямозубой передачи.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.172.189 (0.009 с.) |

 (3.16)
(3.16) (3.18)
(3.18)
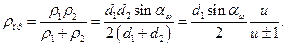
 (3.19)
(3.19) через ZH — коэффициент, учитывающий форму сопряженных поверхностей зубьев;
через ZH — коэффициент, учитывающий форму сопряженных поверхностей зубьев; = Zм — коэффициент, учитывающий механические свойства
= Zм — коэффициент, учитывающий механические свойства = Zz — коэффициент, учитывающий суммарную длину контактных линии для
= Zz — коэффициент, учитывающий суммарную длину контактных линии для 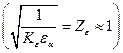 прямозубых передач.
прямозубых передач.
 (3.20)
(3.20)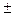 1) и bω =Ψibaaw в формулу (3.20) и некоторых преобразований получим удобную для расчета формулу
1) и bω =Ψibaaw в формулу (3.20) и некоторых преобразований получим удобную для расчета формулу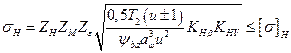 (3.21)
(3.21)
 через вспомогательный коэффициент
через вспомогательный коэффициент (3.22)
(3.22) (или
(или



