
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейная обратная связь - модель Ферхюлста.Содержание книги
Поиск на нашем сайте
Выше был описан случай, когда система отклонялась от своего первоначального положения и стремительно удалялась от него, в рамках этой модели, сколь угодно далеко. Однако мы ожидаем – во всяком случае, модели систем строятся как раз из расчета на это – что, рано или поздно, наша система перейдет в новое состояние. Иными словами, теперь перед нами стоит задача о математическом описании перехода системы из одного состояния в другое. Для построения такой модели зададимся вопросом: а почему вообще возможно «торможение» изменения характеристики системы? Например, это можно сделать следующим образом: как только значение характеристики системы х начнет приближаться к нужному нам новому значению х2, значение управляющего параметра k должно уменьшаться и достигать нулевого значения при х= х2. Другими словами, для описания управления перевода системы в новое состояние, мы должны рассмотреть случай, когда имеется зависимости управляющего параметра от текущих характеристик системы. Как правило, мы получаем при этом нелинейные дифференциальные уравнения. Например, для уравнения (6.1) его модификация выглядит так:
Простейший случай – это когда k(x)=1- x, и мы получаем уравнение, называемое уравнением Ферхюлста или логистическим уравнением (к такому виду можно привести при помощи преобразования координат любую линейную зависимости управляющего параметра от характеристики системы)
Нетрудно видеть, что это уравнение описывает переход системы из «неустойчивого» состояния х=0 в устойчивое состояние х=1 – рассматриваются только положительные значения х. В самом общем случае, отклонения от равновесного – то есть от устойчивого состояния – описываются чаще всего в рамках линейного подхода. Если даже и рассматриваются нелинейные добавки, то они полагаются, в определенном смысле, «малыми» по сравнению с линейными членами. Поэтому можно сделать вывод: для управления посредством отрицательной обратной связи достаточно, как правило, линейного описания. Поскольку линейные методы в математике хорошо развиты, поэтому и неудивительно, что основные успехи в кибернетике (особенно – в кибернетике технической) достигнуты именно в области управления системами с целью сохранения их текущего состояния. Вместе с тем в области кибернетики экономической огромное множество задач носит совершенно противоположный характер: необходимо управлять процессом перевода исследуемой системы в то состояние, которое нам нужно. Следовательно, основным объектом изучения в экономической кибернетике являются нелинейные математические модели. Математический аппарат для их исследования весьма сложен, по этой причине и результатов достигнуто не так много. Впрочем, в рамках технической кибернетики для нелинейных задач результатов также достигнуто весьма мало.
Решение уравнения Ферхюлста (6.4) можно записать в виде
Здесь через х0 обозначено значение характеристики системы в начальный момент времени, при t=0. Соответствующие решения – называемые интегральными кривыми этого уравнения – изображены на Рис.6.1
Возникает вопрос: а можем ли мы говорить в этом случае о наличии обратной связи вообще? Может быть, было бы более корректно говорить о модели системы? Многое зависит от того, какую задачу мы решаем, то есть от цели нашего исследования. Как правило, вопрос о построении модели системы – это не более чем этап в подготовке и выборе системы управления данным социальным или экономическим объектом. Эта мысль станет боле понятной в том случае, когда уравнение Ферхюлста запишется в размерной форме, - то есть так, как оно обычно и получается при моделировании: dx/ dt= ax- bx2= ax(1- bx/ a). В такой форме записи явно введены управляющие параметры a и b, посредством изменения которых мы можем управлять как конечным состоянием системы, так и процессом его достижения. Интерпретация и обобщение модели Ферхюлста: "квота вылова" как модель оптимального управления. Модель Ферхюлста появилась как простейшее обобщение модели Мальтуса на наличие «естественных ограничений» на рождаемость, приводящих к гибели индивидов. Этой моделью часто описывают размножение биологических объектов разного рода – от бактерий и до высших организмов – таких, как рыбы. В связи с последним и рассмотрим на примере рыб организацию системы управления их численностью с учетом вылова. Такая задача отражает наше естественное желание использовать ресурс – в данном случае рыбу – для своих нужд. При этом, однако, мы хотим осуществить управление количеством рыб таким образом, чтобы достичь максимально возможного вылова без того, чтобы рыбы исчезли. Таким образом, мы будем рассматривать задачу об оптимальном использовании природного ресурса. При этом под термином оптимальность понимается, что 1) рыбы нужно вылавливать как можно больше, но 2) ресурс не должен истощаться.
Поскольку наше вмешательство является внешним по отношению к системе, уравнение (6.4) нужно модифицировать. Рассмотрим две простейшие возможности для модификации. Прежде всего – мы можем отлавливать рыбу с постоянно й скоростью, обозначенной с (количество рыб, вылавливаемых в единицу времени, - например, ежегодно). В этом случае уравнение (6.4) примет вид
Из уравнения (6.6) следует, что при с>1/4 количество рыб может только уменьшаться, ибо при этом производная будет всегда отрицательна. Другими словами, если мы отлавливаем ежегодно (в качестве естественного промежутка времени удобно выбрать 1 год – время репродуктивного цикла рыб) более чем 25% от стационарно возможного количества рыб (то есть тех, которые были бы без вылова, - в наших обозначениях их количество равно 1), то рыбный ресурс будет истощен, то есть количество рыб устремится к нулю. При 0< c<1/4 – рыбный ресурс установится на некотором уровне, составляющем какую-то часть от максимально возможного х=1. При этом, однако максимальная квота отлова с=1/4 является неустойчивой (любое ее сколь угодно малое превышение приведет к исчезновению системы – рыб), и поэтому должна быть признана недопустимой. Интегральные кривые уравнения (6.6) показаны на рисунке 6.2.
Может быть, попробуем организовать вылов рыбы по-другому? Например, будем задавать квоту вылова как величину, пропорциональную уже имеющемуся количеству рыбы? Тогда получим уравнение
Здесь величина рх задает скорость отлова рыбы. Из (6.7) очевидно, что имеют место неравенства 0< p<1. При этих условиях в стационарное количество рыб устанавливается на уровне х=В, где В находится как решение уравнения (1- x) x= px. Скорость вылова тогда может быть рассчитана по формуле с=рВ. Зададимся вопросом: когда эта скорость может быть максимальной? Ответ на этот вопрос легче всего найти из геометрических соображений. Точка В находится как пересечение графика квадратичной параболы (1-х)х и прямой рх. Наибольшее значение скорости вылова с=рх равно наибольшей ординате графика функции (1-х)х, а это достигается при х=1/2. При этом значение р=1/2 (необходимо, чтобы значение рх было равно 1/4 - максимальному значению функции (1-х)х, которое достигается при х=1/2. А это достигается, в свою очередь, при р=1/2. Таким образом, для задачи (6.7) максимальная скорость отлова рыбы устанавливается на уровне с=1/4, - однако теперь, как легко видеть из (6.7), при этом устанавливается устойчивое количество рыбы.
Вот мы и привели пример ситуации, когда рассмотрение разных сценариев управления системой – в нашем случае это были разные сценарии отлова рыбы – позволяет достичь устойчивого перевода системы в новое состояние. Конечно, важные для практики задачи не будут, скорее всего, иметь такой простой вид – однако общая методология их решений будет такой же: сначала подбираем подходящую модель системы и формулируем для нее базовую математическую модель. А потом – исследуем разные способы управления, которые могут быть осуществлены в рамках этой модели. Часто для этого приходится явно выделять те допущения, которые были положены в основу базовой модели и исследовать, можем ли мы от них отказаться – и как при этом изменится математическая модель как системы, так и управления этой системой.
Двухкомпонентная модель социально-экономической системы с обратной связью (обобщение модели Лоттка-Вольтерра): математическое исследование, экономическая и социальная интерпретации. Выше были рассмотрены примеры однокомпонентных моделей, задающие обратную связи и допускающие внешнее управление. Теперь перейдем к рассмотрению двухкомпонентной модели. Изложение данной модели ведется на достаточно высоком математическом уровне. Однако именно вследствие этого оно являет собой весьма поучительный пример проведения кибернетического моделирования, которое допускает свое применение к большому количеству самых разных систем. Нас, однако, интересуют прежде всего приложения этой математической модели к социальным и экономическим объектам, и проведение социального и экономического анализа с целью управления такими системами. Весьма важным методологическим обстоятельством является вывод исходной системы уравнений «из общесистемных требований», что как раз наглядно демонстрирует весьма широкий круг возможных приложений полученных результатов. Нелишне также подчеркнуть, что полученные результаты описывают общий случай взаимодействия двух социальных или экономических объектов одного уровня иерархии. Другими словами, если нас интересует задача об описании взаимного влияния двух однородных объектов, или же задача взаимодействия двух компонент, описывающих один и тот же объект – во всех таких случаях мы в качестве базовой придем именно к описанной ниже модели.
|
||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.103.111 (0.012 с.) |

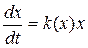 (6.3)
(6.3)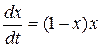 (6.4)
(6.4)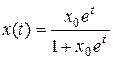 (6.5)
(6.5)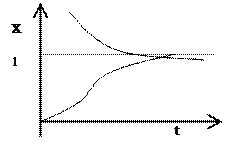
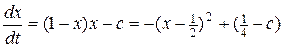 (6.6)
(6.6)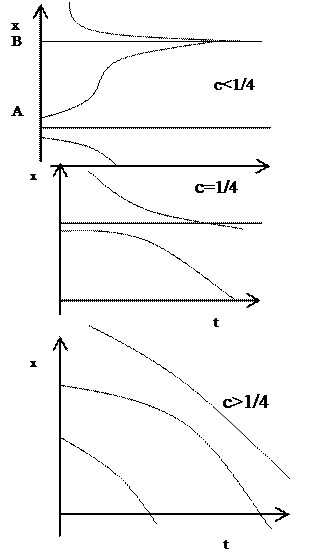
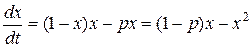 (6.7)
(6.7)



