
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейный случай - модель Мальтуса.
Перейдем теперь к математической форме описания сказанного выше. Рассмотрим систему, которая характеризуется всего одной характеристикой х – такие системы называются однокомпонентными. Пусть состояние системы характеризуется ее значением х0. Из-за внешних воздействий характеристика системы изменилась и стала равна х1. Наиболее простой случай управления – когда мы реализовали такие условия, что скорость изменения координаты оказывается пропорциональной ее отклонению от ее равновесного (стационарного) положения х0. Математически это можно записать так:
Удобнее записывать уравнение сразу относительно изменения характеристики – то есть изменения «координаты» системы Dх. В уравнении (6.1) k – это так называемый управляющий параметр, - в нашем случае число, характеризующее систему и которое мы можем изменять как по величине, так и по знаку – например, сделать его либо положительным, либо отрицательным – при помощи внешних (управляющих) воздействий. Решение уравнения (6.1) записывается в виде
Здесь х1 – значение характеристики х (отклонение от равновесия) при t=0, то есть – в начальный момент времени. Из (6.2) видно, что при k>0 система будет все более удаляться от своего равновесного состояния, характеризуемого значением х0. Наоборот, при k<0 система будет возвращаться к своему равновесному состоянию. Таким образом, в первом случае – при k>0 – имеет место положительная обратная связь, а при k<0 – отрицательная обратная связь. Скорость, с которой будет осуществляться это удаление/приближение, зависит от абсолютной величины управляющего параметра – от | k|. Чем больше эта величина, тем быстрее система удаляется/возвращается к равновесному состоянию. Итак, в рамках этой математической модели мы получаем возможность регулировать – то есть управлять системой посредством: 1. Создания положительной/отрицательной обратной связи. 2. Изменения силы этой обратной связи (величины модуля управляющего параметра | k|). Примером уравнения (6.1), описывающего реальную социально-экономическую ситуацию, является так называемая модель Мальтуса для численности населения. В ее основу заложено «простое и естественное» предположение: прирост количества людей пропорционален их имеющемуся количеству. В этом случае дифференциальное уравнение, описывающее отклонение системы от некоторого начального количества людей N0, может быть записано так: dN/ dt= kN. Конечно, здесь k>0, чтобы имел место именно прирост, а не убыль населения. Решение этого уравнения имеет вид N(t)= N0 exp(kt), - полагается, что при t=0 численность населения становила N0. Как видно из решения, численность населения в такой модели стремительно нарастает, - период удвоения количества населения может быть рассчитан по формуле T= ln2/ k: по демографическим статистическим данным этот период времени сегодня составляет 40 лет. В модели Мальтуса мы получили рост населения в геометрической прогрессии. Вместе с тем известно, что ресурсы, которыми обладает та или иная страна (да и вся планета в целом!) возрастают в прогрессии арифметической. Но тогда приходим к выводу, что, по мере истечения времени, рост населения происходит быстрее, чем прирост ресурсов! Другими словами, относительное количество ресурсов – количество ресурсов, приходящихся на одного человека – с течением времени будет уменьшаться. В этом, собственно, и состоит вывод теории Мальтуса. Этот вывод был им сделан в начале ХIХ века, а в конце ХХ века к этому же выводу пришли и ученые, сформировавшие неформальную организацию под названием «Римский клуб». Конечно, пришли они к нему, используя гораздо более «изощренные» теоретические и математические модели. Собственно, именно в такой простой модели, которая оказалась на удивление мало чувствительной к последующим уточнениям, и кроются причины все учащающихся призывов к ограничению рождаемости (то есть к уменьшению управляющего параметра k). Конечно, это не решит проблемы – но хотя-бы даст время на принятие решений. Может быть, добиться, чтобы k=0 – хотя бы в масштабах всей планеты? Однако, как легко видеть, это значение является неустойчивым: чуть только k станет положительным – начнется опять рост населения, а чуть только оно станет отрицательным – количество населения начнет уменьшаться. Конечно, это произойдет не сразу – но такая организация управления затрагивает уже все население Земли, и поэтому требует совершено новых способов управления и координации в масштабах всей планеты. Осуществить это сегодня невозможно. Так что же делать?! Прежде всего – изучать эту проблему, строить новые модели, рассматривать новые возможные сценарии развития событий.
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.188.64 (0.005 с.) |
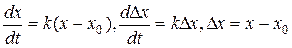 (6.1)
(6.1) (6.2)
(6.2)


