Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аиа как оператор в пространстве компонент информации.Содержание книги
Поиск на нашем сайте
Мы можем ввести 2АИА и другим способом, опираясь на стандартные, принятые в математике, способы. Для этого, пользуясь введенным выше базисов в пространстве информации, запишем произвольную информацию об иерархической системе – точнее, об одном из ее уровней – в следующем виде:
Таким образом, управление может быть представлено в виде линейного оператора G, преобразующего информацию о данном уровне, которая имелась перед осуществлением акта управления Ibefore, в информацию об этом же уровне, которая имеет место после осуществления акта управления Iafter. Это можно записать следующим образом: Легко видеть, рассматривая вектор информации как вектор-столбец, что для этого случая оператор G в матричной форме может быть записан следующим образом: Здесь оператор < k| n> переводит один базисный вектор ik в другой базисный вектор in, а оператор Pkn действует уже только на характеристики (описания) соответствующих компоненты информации, «переводя» их из одного вида в другой. Рассмотрим простейший из возможных случаев, а именно, когда линейный оператор G преобразует одну компоненту информации в другую. Тогда для его матричных элементов получаем:
Таким образом, этот оператор преобразует компоненту информации Ik0 ik0 в компоненту информации In0 in0. Схематически это может быть записано в виде В функциональном виде такой оператор, описывающий управление на определенном уровне в иерархической системе может быть записан как То есть, в виде, характерном для описания кибернетического «черного ящика», на входе и на выходе которого присутствует по одной компоненте информации.
В качестве этого «черного ящика» выступает некий объект, способный осуществлять управление в иерархической системе, далее именуемый двухкомпонентным абстрактным информационным автоматом (2АИА). Этот объект, согласно нашему определению, способен воспринимать одну компоненту информации о данном иерархическом уровне ИСС, а результаты его деятельности на этой иерархическом уровне могут быть описаны также в рамках всего одной компоненты информации. Мы можем определить, в общем случае, набор из 64 возможных операторов – схем управления из 64 разных типов 2АИА. Сюда включается также и управление по схеме «регулятор с обратной связью», который задается условием «вход» = «выход» для компонент информации. Здесь следует учитывать, что в последнем условии знак равенства применяется в нетрадиционной трактовке, поскольку состояния на входе и на выходе, строго говоря, относятся к различным моментам времени, а обратная связь возникает, как результат реакции среды на управляющее воздействие. В качестве естественного обобщения можно для описания управления ввести операторы, которые имеют на входе и выходе по несколько компонент информации (в общем случае, эти количества не равны). Будут ли таким операторам соответствовать реальные объекты – это уже вопрос экспериментальной техники. Каким условиям должны удовлетворять компоненты информации «на входе» в наш оператор Gk0 n0, чтобы он мог быть использован для моделирования управления в реальных ситуациях? Каков должен быть минимальный набор из таких операторов, чтобы с помощью этого набора удалось описать реальные схемы управления? Как мы видели выше, для этого нужно определить введенный нами оператор G как 2АИА.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.62.51 (0.01 с.) |

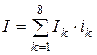
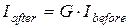
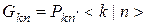
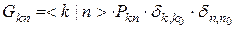
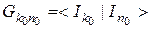 .
.