
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение и постановка задачи
С развитием общества все большее значение приобретает необходимость в разработке информационных систем, позволяющих осуществить прогноз и управление динамикой развития социально - экономических систем (СЭС) различного уровня иерархии. Под СЭС в настоящей главе понимается совокупность однородных объектов социально - экономического процесса (социальных и/или экономических отношений) - начиная от совокупности отдельных людей и заканчивая обществом в целом. Среди важнейших задач, без решения которых невозможно адекватное управление СЭС, ключевое место занимает проблема нахождения критериальных соотношений, выражающих основные закономерности динами развития СЭС. Без выработки таких критериев разработка количественной формализации описания СЭС и математических моделей для управления ними будет чрезвычайно затруднена. Как правило, формализованные критериальные соотношения базируются на результатах рассмотрения конкретных моделей, описывающих СЭС [2]. Высокий уровень сложности таких моделей (см., например [3]) обусловлен, как правило, следующими причинами [4] (впрочем, в последних главах книги описан вариант подхода, позволяющий разрешить эти проблемы): · Отсутствием четкого понимания разнообразных процессов, происходящих в СЭС разного уровня иерархии, а также единого подхода к их описанию. · Отсутствием четких критериев для выделения объектов социально - экономического процесса как единой СЭС. · Трудностями принципиального характера, связанными с необходимостью введения в рассмотрение, учета и формализации так называемого “человеческого фактора” со всем комплексом специфических эффектов, вносимых им в социально - экономический процесс. Среди важнейших из них необходимо выделить: способность Человека синтезировать новую информацию, имеющую коммерческую ценность; наличие существенной, изменяющейся со временем вариабельности в свойствах, целях, задачах, откликах и т.п. отдельных людей; наличие вариабельности в способности отдельных людей как участвовать в социально - экономических процессах, так и влиять на них; и т.д.. Указанные причины (которые перечислены далеко не все!) привели к тому, что подавляющее большинство современных математических моделей описания динамики СЭС ориентированы на использование их результатов так называемыми ЛПР - людьми, принимающими решения (например, чиновников разного уровня иерархии, менеджеров, политиков и т.п. - см., например [5]). Однако при этом ЛПР часто оказываются перед лицом необходимости принимать решения практически “вслепую”, ибо большинство из них, не являясь специалистами в области математического моделирования (математической кибернетики!), просто не знают границ применимости каждой отдельной модели, положенной в основу той или иной экспертной системы. Наконец, многие из таких ЛПР не являются координаторами (см. последние главы книги), то есть они принимают решения действительно "вслепую"!
Таким образом, одним из возможных перспективных подходов к описанию СЭС является следующий. На первом этапе - создание блока математических моделей, описывающих ключевые особенности динамики СЭС, то есть характерные для СЭС любого уровня иерархии. В силу необходимости отражения самоорганизационных свойств СЭС, эти математические модели должны являться нелинейными и стохастическими, и ориентированными на выработку критериальных закономерностей. В определенном смысле речь идет о создании совокупности неких абстрактных структур математического характера, на базе которых может быть проведено адекватное описание СЭС. Далее, на втором этапе, направление исследований разбивается на два потока: во-первых, на создание математических моделей, формализующих необходимые пользователю понятия, термины, количественные закономерности и т.п., а также связи между ними (например, поле законодательных нормативов) во введенные на первом этапе абстрактные структуры. Этим достигается унификация подхода всей совокупности разнородных по составу ЛПР к описанию результатов своей деятельности, а также - и это чрезвычайно важно - нахождение синергетического, нелинейного эффекта от своих совокупных, совместных действий. Во-вторых, на построение адекватной реальности математической модели для описания взаимодействия тех абстрактных структур, которые были введены на первом этапе. Собственно, только на этом этапе и может идти речь о построении адекватной реальности математической модели для описания СЭС. Вероятно, многие попытки описания динамики СЭС были обречены на неудачу уже на самом этапе постановки задачи, ибо пытались строить соответствующий формализм непосредственно сразу уже на первом этапе. Весьма важным является то, что на втором этапе исследования могут идти параллельно по обоим направлениям, что благоприятствует скорейшему внедрению полученных результатов в практику.
Некоторые результаты, полученные в этом направлении, были ранее описаны в [6]. В этой главе будет построен класс математических моделей, ориентированных на описание состояний СЭС разного уровня иерархии, в котором находят количественное выражение некоторые “наивные” термины, понятия и т.п., широко используемые в вербальном виде - особенно в современном политическом словаре. Фактически, в здесь представлена модель, способная описать усредненное состояние всей экономики, - то есть усредненное состояние всей иерархической экономической системы в целом для данной страны. Итак, выше перед нами поставлено описание проблемы, то есть тот класс задач, который следует решить. Описаны как имеющиеся результаты, так и трудности, вследствие которых задача не могла быть решена ранее, при использовании прежних подходов. Следовательно, решение такой задачи требует развития новых подходов, то есть - построения новых моделей. Отметим, что и само описание проблемы сделано пока что только на вербальном уровне, - дальнейшее продвижение в области моделирования требует уточнения и детализации предлагаемых моделей. Модель В основу описания динамики единичного представителя (далее -“объекта”) СЭС данного уровня иерархии положим следующие соображения, которые можно назвать также и “аксиомами” А1. Деньги (финансы, ресурсы – сведенные к единому выражению, и т.п.) являются мерой информации, которой обладает рассматриваемый объект. “Стоимость” информации определяется посредством самосогласования через всю иерархическую систему СЭС (наибольший вклад в нее вносит, как правило, СЭС наиболее высокого уровня иерархии - государство). А2. Способность к синтезу (рождению) новой информации Человеком приводит к тому, что для рассматриваемого объекта его способность к увеличению финансов увеличивается с возрастанием их количества, тем самым образуя кольцо положительной обратной связи (более подробно о кольцах положительной и отрицательной обратной связи см. в следующей главе): “больше информации - больше финансов - больше информации” (ср. с английской пословицей “ деньги делают деньги ”). Это также достигается путем самосогласования. А3. Существует необходимость “расходования” денег (финансов, информации) для продолжения функционирования рассматриваемого объекта (что формирует тем самым кольцо отрицательной обратной связи). Интенсивность расходования возрастает с ростом денежной массы быстрее, чем ее прирост. Такое расходование также замыкается самосогласованием через всю иерархию СЭС (например, через налоги - как федеральные, так и местные). А4. Поскольку способность Человека синтезировать (создавать) новую информацию (следовательно, и новые финансы) носит ярко выраженный индивидуальный характер, то процесс функционирования совокупности рассматриваемых объектов должен носить стохастический характер.
Эти предположения могут быть строго обоснованы в рамках теории, кратко описанной в последних главах настоящей книги. Теперь мы перешли к построению модели для типичного объекта, которые являются «действующими лицами» нашей системы. Мы – уже на вербально-логическом уровне – описали набор характеристик таких объектов, которые в последствии будут отражены в рамках математической модели. Подчеркнем характерную особенность: «единичные объекты», составляющие нашу систему, могут спонтанным образом проявлять некоторые свойства, - по этой причине мы уже на этом этапе приходим к выводу, что адекватное реальности описание должно быть произведено только на стохастическом уровне. Другими словами, в качестве математического аппарата мы выбираем теорию случайных процессов, стохастической дифференциальные уравнения, и т.п., а в качестве экспериментально проверяемых объектов у нас будут выступать либо плотность вероятности (если удается ее получить – это идеальный! случай), либо отдельные ее моменты – средние значения, дисперсия и т.п. (это, конечно, похуже – но тоже может быть использовано в экспериментальной и практической деятельности. Математически сказанное в А1-А3 можно описать уравнением где R(m)>0 и T(m)>0 - некоторые (монотонные) функции, причем $m0: "m>m0 ÞT(m)>R(m) (вследствие А3 функция T(m) при больших m становится больше, чем R(m)). Здесь обозначено через m массу финансов (информации), которой обладает рассматриваемый объект социально - экономических отношений в настоящее время. Условие монотонности R(m) и T(m) приводит к тому, что уравнение (1) имеет только одно стационарное положение равновесия, которое является устойчивым и в котором рассматриваемый объект характеризуется значением m0: R(m0) = T(m0) (2) В функциях R(m) и T(m) должна найти отражение вся иерархическая система СЭС. Поскольку в настоящее время вид этих функций неизвестен, дальнейший анализ (1) возможен только с привлечением соображений модельного, феноменологического характера. На этом этапе мы не рассматривали аксиому А4, то есть, мы пока что занимаемся моделированием описания динамики единичного объекта нашей СЭС. Мы пытаемся «выжать» из известной нам информации (включая те предположения, которые кажутся нам «естественными» для таких объектов) всю ту информацию, которая может найти отражение в математической форме записи. Подчеркнем: именно на этом этапе часто и возникает необходимость обращаться к новым для себя математическим теориям. На данном этапе также видно, что мы, рассматривая такую – на первый взгляд «простую» задачу – вынуждены, тем не менее, строить целую иерархическую систему моделей. Чрезвычайно важно, чтобы уже на сейчас, строя эти иерархические модели, мы задумались над тем, как мы будем брать необходимые нам данные из эксперимента.
При моделировании сложных иерархических систем живой и неживой природы для описания их свойств или закономерностей часто используют так называемые “аллометрические закономерности”, когда искомая закономерность представляется в виде степенной зависимости от своих параметров (для биологических объектов см., например [7], а для технических [8]). В физике подобные закономерности обычно возникают вследствие требований так называемой масштабной инвариантности, когда некоторые свойства системы инвариантны относительно преобразований масштаба рассматриваемых явлений (см. [9]). Как правило, такие зависимости выражают найденные из статистических данных закономерности. Почему они так распространены всюду – включая и экономику? Ответ на этот вопрос достаточно прост, хотя он и может быть неожиданным. Социальные и экономические системы занимают «большие» промежутки в изменениях своих параметров. Например, годовой доход - от нескольких тысяч единиц (отдельный человек, малое предприятие) и до миллионов или даже миллиардов (3 –6 порядков). Количество людей, задействованных в них – от единиц (семья) и до миллионов (область, мегаполис) – и в этой области параметров также до 6 порядков. Статистические данные просто невозможно наглядным образом представить при линейном масштабе координат! Приходится прибегать к так называемой «дважды логарифмической» системе координат: по обеим осям откладываются логарифмы характеристик СЭС. А прямая линейной регрессии, проведенная через экспериментальные точки – это как раз и есть степенная функция! Как видим, причина, по которой данные выражаются именно в такой форме, имеет технической характер. Подчеркнем чрезвычайно важное обстоятельство, - одновременно мы выявили те условия, при которых такая форма обработки экспериментальных данных является оправданной (границы применимости этого способа!): для этого оба параметра, связь между которыми мы находим, должны изменяться «в широких пределах». Отметим, что выполнения последнего свойства можно ожидать и от объектов социально - экономического процесса в предположении, что их способность как к приросту массы финансов, так и к их трате инвариантны относительно преобразований масштаба величины m для СЭС, принадлежащих данному уровню иерархии (естественно, конкретная их параметризация для каждого уровня иерархии своя).
Итак, проведем дальнейшее рассмотрение, предполагая, что
R(m) = cma T(m)=dmb (3)
При этом b>a вследствие А3. Здесь сама способность рассматриваемого объекта социально - экономического процесса к приобретению и расходованию финансов определяется коэффициентами a и b, которые будут зависеть как от принадлежности объекта к тому или иному уровню иерархии СЭС, так и от всей их иерархической совокупности (например, будут регулироваться государством). На Рис.5.1 представлены данные (Украина, январь 1996 года) системе налогообложения доходов граждан - видно, что в диапазоне 1,6<m<200 единиц необлагаемого дохода она хорошо аппроксимируется зависимостью T(m)=0,045 × m1,38 (для России на тот же период времени в диапазоне 1<m<8 получим T(m)=0,17 × m1,18). Интенсивности процессов приобретения и расходования финансов в рамках аппроксимации (3) будут определяться величинами параметров c и d, а стационарное состояние достигается при m0=(c/d)1/(b-a). Модель (1) - (3) выведена на основании А1 - А3. Для того, чтобы она удовлетворяла также и А4, необходимо учесть вариабельность свойств и возможностей человеческой компоненты социально - экономического процесса. Для заданного объекта это проявляется двумя путями. Во-первых, вследствие внутренних для рассматриваемого объекта причин - например, связанных с его кадровым составом (успехом в подборе людей, способных создавать новую информацию - координаторов), а также от профессионального уровня этих людей (своего рода неравномерность распределения таких людей по фирмам). В результате разные объекты социально - экономического процесса для данного уровня иерархии будут различаться своими константами с. Во-вторых, вследствие причин внешних для данного класса объектов - например, вследствие локальной (территориальной) вариабельности законодательного поля, регулирующего налоговую политику. В результате разные объекты будут различаться своими константами d. Отметим, что учет статистических закономерностей должен быть проведен в рамках ансамблевого подхода, когда рассматривается целый класс объектов для СЭС заданного уровня иерархии. На этом этапе мы переходим от рассмотрения одного объекта к рассмотрению уже многих подобных объектов. Это обусловлено тем, что мы уже знаем, что нам будет нужна плотность вероятности. А ее можно получить только двумя способами. Либо, во-первых, отслеживать один объект – одну СЭС – «достаточно длительное время, что практически неосуществимо по «техническим соображениям»: например, если нас интересует плотность вероятности годового дохода фирмы, то нам пришлось бы собирать данные о нашей фирме на протяжении около 1 тысячи лет! Либо, во-вторых, одновременно собрать данные о большом количестве сходных фирм, - и получить искомую плотность вероятности: таких фирм должно быть также около тысячи – но эта задача уже вполне выполнима! У читателя может возникнуть вопрос: а совпадают ли эти две плотности вероятно, полученные столь разными способами? Этот вопрос достаточно хорошо изучен в рамках теории вероятности и математической статистики – есть даже научная дисциплина под названием «эргодические теории», и ответ на этот вопрос является положительным. Можно даже сказать, что положительность ответа на этот вопрос гарантируется всем опытом развития теории вероятностей и математической статистики. Хотя в общем случае обе причины учета вариабельности свойств Человека действуют совместно, далее для простоты будем рассматривать их раздельное описание. Таким образом, приходим к стохастическим моделям
где для модели (А) d=const и m0= l1/(b-a), а для (В) - c=const и m0= w1/(a-b). В (А) и (В) произведены соответствующие преобразования. Функции xt и ht являются стохастическими. Здесь мы вынуждены прибегнуть к раздельному рассмотрению двух случаев по причинам уже математического характера. Конечно, было бы очень интересно – и, главное, это было бы более адекватно ситуации! – рассмотреть совместный учет обоих причин. Но математический аппарат, который был бы необходим для этого, является чрезвычайно сложным. Более того: многие результаты было бы возможным получить только путем компьютерного моделирования, - например, численного расчета. И только в нашей постановке получаются аналитические, то есть выраженные в формульном виде, зависимости. Это позволяет провести качественный анализ большого количества возможных ситуаций – и поэтому такой возможность никак не следует пренебрегать! В общем случае модели (А) и (В) приводят к тому, что совокупность объектов данного уровня иерархии для социально-экономических процессов характеризуется распределением плотности вероятности P(m,t). Если шум xt (или ht, соответственно) является стационарным, то вследствие условия b>a имеем P(m,t) ® Ps(m), причем, в общем случае, вид Ps(m) будет определяться лишь статистическими свойствами xt (ht) и величинами a, b и m0. Дальнейшее рассмотрение проведем в пренебрежении переходными процессами - то есть для Ps(m). Общими свойствами моделей (А) и (В) являются такие: I. Обе модели допускают обезразмеривание, то есть Ps(m) можно представить в автомодельном виде Ps(x) по безразмернойпеременной x=m/m0 (естественно, при соответствующем обезразмеривании функций x t (h t)). Это обстоятельство является весьма важным, ибо позволяет сравнивать между собой поведение разных СЭС (но обладающих одинаковыми параметрами a и b). Распределение Ps(x) зависит тогда только от a, b и вида (точнее - структуры) обезразмеренного шума x t (h t). Вследствие этого появляется возможность разработки новых критериев для классификации и сравнения состояний СЭС, принадлежащих к разным уровням иерархии. Так, это свойство рассматриваемых моделей позволяет отвлечься от видов национальных валют, их конвертации и т.п., и сравнивать между собой объекты-СЭС одинакового уровня иерархии, находящиеся даже в разных странах (и, соответственно, в разных условиях). Вследствие этого появляется возможность также для количественного сравнения между собой состояний СЭС из разных стран и синтеза систем оптимального управления развитием СЭС в выбранном направлении (например, появляется возможность количественного сравнения показателей качества жизни граждан (малых фирм и т.п.) для разных стран). II. Модели (А) и (В) являются инвариантными относительно группы преобразований m ® N: m=kNn, где k>0 и n>0 - соответствующие константы. Это позволяет применять как сами модели (А) и (В), так и произведенные на их базе интерпретации, к различным характеристикам, описывающим рассматриваемые объекты социально - экономического процесса (например, выполнение соотношений такого вида естественно ожидать для численности N сотрудников фирмы в зависимости от имеющихся в ней запаса финансов). Естественно, при такой группе преобразований параметры модели преобразуются как aN=1+n(am - 1), bN=1+n(bm - 1), l N = l m a-b, x t N =ka-b x t m (для примера выписаны лишь соотношения для модели (А); для модели (В) такие соотношения выглядят аналогично). Весьма важным является также то обстоятельство, что все результаты (например, распределения Ps(x)), полученные для одной какой - нибудь характеристики рассматриваемого объекта могут быть пересчитаны для любой (!) другой характеристики, связанной с первой рассматриваемым групповым соотношением, - а выводы автоматически (!) являются верными. Иными словами, мы получили новый способ установления инвариантности и эквивалентности как между отдельными характеристиками рассматриваемого объекта, так и между объектами разных уровней иерархии, а также - новый способ восстановления целого класса характеристик объекта по распределению одной из его характеристик! Пример В качестве примера рассмотрим аналитически точно решаемый случай, когда xt и ht являются белым шумом с интенсивностью < xt2>= s2 (< ht2>= s2 соответственно). Здесь опять приведена система новых ограничений, и опять – математического характера. По сути, мы до сих пор все еще производим последовательное уточнение модели! Конечно, при этом сужается общность ее применения – но зато мы получаем возможность провести более глубокий анализ. Фактически, мы размениваем глубину понимания на уменьшение общности (в ущерб общности) – то есть детализируем ситуацию, делая ее все более конкретной. Такое положение вещей характерно для любой профессиональной области в области социального и экономического моделирования. В результате мы получаем иерархически связанную систему моделей исследуемого социального или экономического объекта (процесса, явления и т.п.): на самом верху расположены общие модели, а внизу находятся модели, обладающие более узкими границами применимости (но позволяющие провести количественный анализ ситуации). Формирование такой «пирамиды моделей» – неотъемлемая составляющая процесса познания мира человеком. Тогда из уравнений (А) или (В) обычным образом строится уравнение Колмогорова - Фоккера - Планка в соответствующей нашему случаю интерпретации Стратоновича (все необходимые математические см. предыдущем параграфе, а также в [10]), из которого находим
для модели (А) и
для модели (В), соответственно. В (4) и (5) Сi - соответствующие нормировочные константы. Для рассматриваемого примера асимптотика P(m,t) ® Psa(b)(m) справедливо независимо от вида начального распределения P(m,t=0). Модель (А) при 0<a £1 допускает так называемые индуцированные шумом переходы, когда форма Psa(m) изменяется скачком (в нашем случае - от колоколообразной (одномодальной) до монотонноспадающей) при непрерывном изменении интенсивности шума s2 (в нашем случае - при увеличении s2 сверх s2с), однако здесь мы эти эффекты рассматривать не будем. Отметим общее свойства полученных Psa(b)(m): 1) При малых интенсивностях шума s 2 (то есть при малой вариабельности вклада от человеческой компоненты СЭС) Psa(b)(m)» d (m-m0), где d (x) - сингулярная дельта - функция Дирака. 2) С ростом s 2 ширина D распределений Psa(b)(m) увеличивается (на Рис.5.2 приведен пример зависимости относительной ширины D (измеренной на полувысоте) от безразмерной интенсивности шума s 0 2 для автомодельного распределения Psa(x); выбраны значения параметров a=2/3, b=1), а положение максимума m+ распределения сдвигается к нулю.
Модели (А) и (В) в приближении белого шума будут хорошо описывать главный вклад в экспериментально измеренные Pе(m), сосредоточенный в окрестности максимума. “Хвосты” распределений Pe(m) будут формироваться из сравнительно малого количества объектов, поэтому в рамках модели белого шума в них нельзя должным образом учесть вариабельность индивидуальных свойств людей (можно сказать, что в “хвостах” Pe(m) проявляются “более яркие индивидуальности”). Интересно, что объекты вблизи максимума Pe(m) естественно отождествить со “средним классом” - поэтому известные нечеткие вербальные описания типа “для устойчивости общества необходимо наличие значительной прослойки среднего класса” с использованием (4) и (5) можно сформулировать в виде четких и однозначных математических критериев. Ниже приведем примеры некоторых стратегий управления СЭС, основанных на предложенном подходе и модели белого шума. Общую тенденцию развития СЭС можно сформулировать следующим образом: рост благосостояния людей при условии отсутствия напряженности в обществе. В рамках моделей (А) и (В) росту благосостояния соответствует рост m0, а “отсутствию напряженности” соответствует условие “оптимальной относительной ширины” D для Ps(m) - в нашем примере оно соответствует “оптимальности” величины относительной интенсивности шума s 02 для автомодельного вида распределения по доходам Ps(x). В нашем примере для относительной (безразмерной) интенсивности шума нетрудно получить для модели (А) выражение
а для модели (В) - Весьма интересно и нетривиально поведение s 02 при s2=const с возрастанием m0.
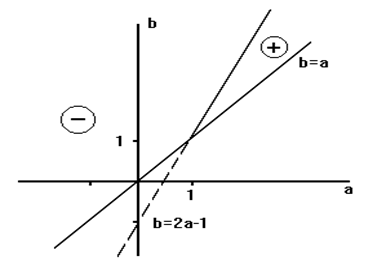
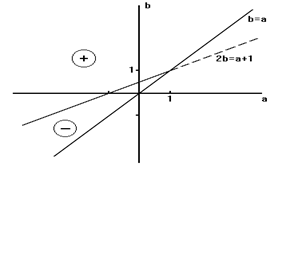
На Рис.5.3. представлено поведение s02 при возрастании m0 при s2=const (модель (А), формула (6)). В области “+” s02(m0) монотонно возрастает, что приводит к уширению Ps(x), и выполнение критерия s02 ®opt требует уменьшения величины s2, то есть выполнимо лишь тоталитарными методами. В области “-” состояние СЭС можно считать “устойчивым” в том смысле, что s02(m0) монотонно убывает, и, следовательно, при возрастании m0 допускаемо увеличение s2 - то есть усиление демократических тенденций в обществе, а также создаются условия для развития научно - технического прогресса.
Другими словами, на Рис.5.3 для модели (А) представлено поведение s 02 в плоскости параметров а и b. Условие b>a выделяет область параметров, обеспечивающих наличие стационарных распределений Ps(m). Прямая b=2a-1 разбивает эту область на две подобласти, в одной из которых достигается монотонное убывание s 02(m0) при s2=const (обозначено знаком “-”), а во второй - монотонное возрастание при тех же условиях (обозначено знаком “+”). Для модели (В) - см. Рис.5.4. Отсутствие напряженности в обществе достигается через механизм демократии, то есть путем гарантирования равных возможностей для его членов. Но научно - технический прогресс подразумевает все более полное вовлечение всех способностей, качеств, свойств, возможностей Человека в социально - экономические процессы. В результате это приводит к возрастанию вариабельности в социально - экономических проявлениях свойств людей - и, как следствие - к увеличению интенсивности шума s2. Таким образом, развитие общества сопровождается увеличением как m0, так и s2, но при таком увеличении должно, тем не менее, сохраняться “оптимальное” значение s 02=opt (где opt - значение относительной интенсивности шума, которое находится опытным путем). Отметим, что в качестве меры устойчивости рассматриваемого (данного) состояния общества можно тогда выбрать, например, критерии вида
или же подобные им. Как видно из Рис.5.3 и Рис.5.4, управление устойчивостью общества должно осуществляться таким образом, чтобы при возрастании m0: 1) значения параметров a и b постоянно поддерживались в области, где s 0 2 (m0) монотонно убывает с ростом m0 (то есть в области, обозначенной знаком “-” на Рис.3 и Рис.4) - это дает возможность увеличивать уровень демократии в обществе и образованности его граждан; 2) добиваться значений s 0 2 ® opt (то есть d ® 0 или g ® 0, соответственно); 3) добиваться значений {(1-a)c}-1m01-a £ T» 3 ¸ 5 лет (соответственно при a=1: c-1ln(m0) £ T) для отдельных людей (и соответствующих значений T0 для каждого иерархического уровня). Это условие означает, что каждый человек имеет возможность – при данном состоянии экономических «правил игры» в обществе – радикально изменить свое благосостояние (например, перейти их «бедного» в «зажиточное» состояние). Отметим, что условия I и III являются в определенном смысле конфликтными, так как условие I легко достигается путем возрастания c, а условие III, переписанное в виде c(1-b)/(b-a)d-(1-a)/(b-a) £T, может быть далеко не всегда совместимо с ростом с (однако при b>1 (см. ниже) оно будет выполняться “автоматически” при d=const). Общее обсуждение Рассмотрим каналы, посредством которых общество (государство) может изменять величины, характеризующие рассмотренные модели и приведенный выше Пример - a,b,c,d и s2. Отметим. что все эти параметры могут изменяться при переходе к иному иерархическому уровню, и к тому же конкретная интерпретация этих параметров, как и способов управления, может быть разной для разных иерархических уровней. Теперь, имея уже аналитическую модель социальной или экономической системы и проведя качественный анализ этой математической модели, мы переходим к этапу социальной и/или экономической интерпретации полученных результатов. Другими словами: если ранее мы, исходя из реальной ситуации, «поднимались» от нее в мир абстракций, то теперь мы уже совершаем «спуск» из мира абстракций к миру реальному. Мы, по сути, сейчас готовим методологию использования наших результатов. Для начала – нас интересует, каким образом мы можем интерпретировать те или иные закономерности в рамках нашей модели: как правило, это приводит к формированию конкретных методик ведения экспериментальной деятельности в области социологии и экономики. Как отмечалось выше, член R=cma определяет способность данного объекта к приращению дохода. При этом параметр c определяется индивидуальными (то есть - изменяемыми от объекта к объекту) свойствами данного объекта, тогда как a - всей иерархической системой СЭС в целом. Например, для нижнего иерархического уровня - совокупности отдельных людей - с будет зависеть от их личных способностей, тогда как a - будет определяться, например, наличием инфраструктур, способствующих как получению (синтезу) новой информации и ее последующей обработки, так и способствующих “реализации задумов”. Интересно, что каждый иерархический уровень отличается от других “степенью дискретности времени ” характерных для него переменных. Поскольку при наличии дохода (точнее - свободных денег) возможность доступа к информации (ее объему, точности и адекватности, надежности переработки и т.п.) увеличивается, то можно ожидать, что a>0, то есть доход возрастает пропорционально имеющемуся (ср. “деньги делают деньги”). Вместе с тем, трудно ожидать, что в нормальной экономике могут достигаться значения a ³1, при которых “начальный капитал” вырастал бы взрывообразно (впрочем, это затруднение легко преодолевается при b>1). Итак, для отдельного человека ожидается 0<a<1 - впрочем, пока что это не более чем эвристическое соображение. Для крупных корпораций - наоборот, можно ожидать, что с ростом дохода способность денег “приносить деньги” будет падать - что достигается при a<0. Таким образом, можно ожидать, что с ростом уровня иерархии происходит уменьшение a. Что же касается с, то ожидаемая картина как раз противоположна: ожидается его возрастание (одновременно - с возрастанием s2 : ибо основной “прорыв” крупных компаний достигается, как правило, благодаря деятельности “наиболее гениальных” людей, - а их всегда мало!). Эвристическим подтверждением этому может служить также необходимость возрастания характерного времени {(1-a)c}-1m01-a=T (характерное время для изменения единичным объектом-СЭС своего экономического состояния) с ростом уровня иерархии.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.211 (0.066 с.) |
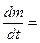 R(m) - T(m) (1)
R(m) - T(m) (1)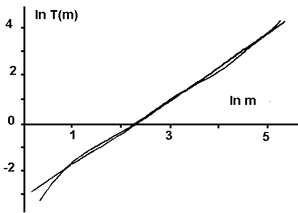
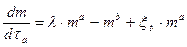 (A)
(A)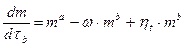 (B)
(B)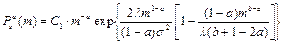
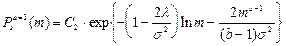 , a=1 (4)
, a=1 (4)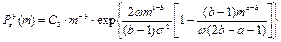
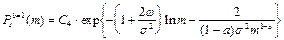 , b=1 (5)
, b=1 (5)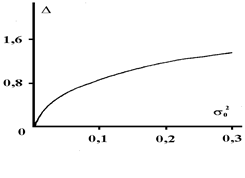
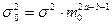 (6)
(6)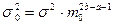 (7)
(7)
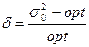 , dÎ[-1,¥) (8)
, dÎ[-1,¥) (8)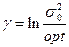 , gÎ(-¥, ¥) (9)
, gÎ(-¥, ¥) (9)


