Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация состояний системы.Содержание книги
Поиск на нашем сайте
Вначале рассмотрим общую проблему классификации множества возможных состояний социально-экономических систем – СЭС. Оптимальным языком для такого описания является язык теории множеств и топологии: действительно, каждое состояние есть класс характеристик, который характерен относительно некоторого множества внешних воздействий (например, множества изменений управляющих параметров). Проведенное ниже описание имеет гораздо более широкие рамки применимости и выходит далеко за рамки задач описания и классификации социальных или экономических систем. В частности, подобные модели широко используются в экологии для описания оптимального управления количеством тех или иных животных или для описания влияния воздействия ядохимикатов на систему связанных между собой трофическими (пищевыми) цепями популяций. Ниже описана математическая структура, которая является адекватной для проблемы нахождения и классификации всех возможных состояний СЭС. В качестве примера реализации общего подхода рассмотрен случай простейшей для описания динамики СЭС на макроэкономическом уровне. Изложение ведется на "физическом" уровне строгости, однако восстановление точного "математического" уровня описания не представляет, как правило, затруднений.
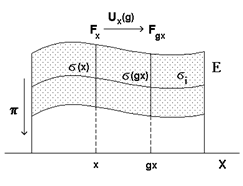
Рассмотрим следующую математическую структуру (Рис.6.3). Введем в рассмотрение пространство E всех возможных текущих значений параметров, характеризующих СЭС во всех точках пространства - времени x Î X (город, страна, континент и т.п.). Тогда множество X можно рассматривать как базу, над точками которой при помощи отображения p-1 восстанавливается некий слой F x Ì E возможных значений параметров СЭС. Переход к иной точке пространства - времени осуществляется при помощи (группового или полугруппового) преобразования g Î G на точках базы g: x ® g x Î X. Слой F x при таком преобразовании переводится в слой F g x с помощью отображения U x(g): F x ® F g x Ì E. Заданная конкретная реализация СЭС выделяется некоторой точкой F i Î F x и при преобразованиях g Î G на точках базы задает сечение s i(x). В математическом смысле описанная структура являет собой пример главного расслоения над базой X, – см., например, книги 1) Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия.- М.:Наука,1979.-760с. и 2) Рохлин В.А., Фукс Д.Б. Начальный курс топологии.-М.:Наука,1977.-488с. Введем теперь операцию e установления соотношения социально - экономической эквивалентности в пространстве E s всех орбит сечений s(x). Тогда все возможные состояния СЭС могут быть классифицированы при помощи (частично - упорядоченного) множества - "спектра состояний СЭС", которое эквивалентно фактор - множеству S= E s e. С учетом вышесказанного моделирование социально - экономических явлений можно производить по следующей схеме: · Задать пространство E. Его определение должно быть единым (универсальным) и пригодным для широкого класса задач моделирования СЭС. · Задать оператор p проектирования на базу X (выбор базы, как правило, диктуется спецификой задачи), с помощью которого выделяется слой F x над данной точкой базы x Î X (это производится с учетом возможности практического определения необходимых параметров). · Задать группу G, которая будет отражать необходимый уровень пространственно - временного рассмотрения. · Установить вид отображения U x (g): F x ® F g x, где g Î G (в некотором смысле U x (g) можно назвать оператором "допустимых сценариев"). · Найти оператор выделения сечений s (x) и построить пространство E s орбит сечений (этот этап по своей сути является чисто математическим и может быть сведен к некоей алгоритмической вычислительной процедуре). · Ввести соотношение e эквивалентности орбит в пространстве орбит E s (некоторые предпосылки для выбора соотношения эквивалентности могут быть взяты даже из самой структуры пространства E s). · Классификация всех возможных состояний СЭС производится с помощью фактор - множества S = E s e. В рамках приведенной математической структуры, ориентированной на нахождение спектра состояний СЭС S и на его классификацию однозначный смысл приобретает и термин "процесс" применительно к СЭС, который понимается как переход СЭС от одного состояния к другому. Рассмотрим пример реализации описанной выше процедуры, который можно назвать моделью взаимодействия "связанных" и "свободных" финансов в замкнутой СЭС. Как уже отмечалось выше, описанные в этом разделе результаты имеют гораздо более широкую область применимости, - однако в целях определенности мы будем вести изложение применительно к СЭС. Вначале необходимо рассмотреть те особенности, которые связаны с информационной динамикой в СЭС, ибо только в социальной компоненте может произойти "рождение - синтез" новой информации, важной в экономическом плане. В финансовом отношении проблема "ценности" информации имеет два измерения. Во-первых, в данное количество информации вложено количество финансов, затраченных на ее получение. Конечно, это количество финансов является различным для разных состояний и структур СЭС. Во-вторых, и это главное, эта синтезированная, "экономически - значимая" информация имеет также и независимое финансовое измерение, которое может быть выражено посредством "прибыли" от ее внедрения. Это последнее финансовое измерение также не является инвариантным и зависит от возможностей СЭС по адаптации данной информации и определяется как социальными особенностями (например, наличием специалистов), так и экономическими (например, наличием инфраструктуры, способной перевести эту информацию на технологический уровень, то есть "внедрить" ее). Напомним, что частично эти вопросы были рассмотрены ранее в этой книге, - приложение к экономической ситуации см., например, в главе 5. Таким образом, финансы имеют также и информационное измерение – «информационную» компоненту, которая сильно связана со спецификой переработки и синтеза информации Человеком, и которая не подчиняется законам сохранения. В общем случае всю совокупность финансов (ресурсов, денег и т.п. – для краткости будем далее использовать для всего этого комплекса термин «финансы») можно разделить на два основных класса - на "связанные" и "свободные" финансы. Через с вязанные финансы обозначим ту часть финансов, которая вложена в производство новых финансов (например, в технологии, обучение, создание соответствующих инфраструктур и т.п.) и поэтому уже неспособных к движению. Иными словами, связанные финансы уже "овеществлены" и привязаны к неким материальным объектам и структурам. То есть - эта компонента связана с той информацией, которая как раз сейчас проходит социализацию, - то есть именно с той, которая как раз сейчас переводится в социальный или экономический норматив. Под свободными финансами понимается та их часть, которая подвижна и может быть переведена в связанное состояние (например, путем вложения их в новые технологии). В свободные финансы входит также и "информационная" компонента, которая синтезирована в СЭС вследствие информационной деятельности Человека. Можно сказать и так: свободные финансы это то, что может быть вложено в координаторов (см. главу 10). В качестве ее "финансового измерения" можно взять, например, "среднюю прибыль" при внедрении этой информации с учетом данной структуры СЭС (весьма важным является то обстоятельство, что в разных СЭС (например, в разных государствах) финансовое измерение одной и той же новой синтезированной информации будет разным - например, эта величина возрастает при наличии в СЭС инфраструктур, ориентированных на доводку и внедрение информации. Вследствие вышесказанного связанные финансы Ф i и свободные финансы Ф c являют собой независимые компоненты финансового поля в макроэкономике: для них, в частности, отсутствует "закон сохранения", то есть Ф i t + Ф c t ¹const. Замкнутые СЭС. Теперь можно перейти к реализации общей математической структуры для описания макроэкономических процессов в замкнутой СЭС. В качестве базы естественным образом выбирается время: X= T. На базе T зададим дискретную группу G (дискретную, например, вследствие естественной дискретизации представления социально - экономической статистики), которую можно отождествить с группой целых чисел Z. Так как в главном расслоении производится отождествление базы и группы, то T= Z. В качестве слоя F x выбираем прямое произведение Ф i t ÄФ c t. Тогда для нашей модели E=Ф i ÄФ c Ä T, а p является оператором проектирования на ось T. Оператор U x(g), переводящий один слой в другой, для нашей модели будет тождественным, что отвечает неизменным "правилам игры". Оператор, задающий орбиту сечения по заданному "начальному значению" Ф i t=0 и Ф c t=0 в общем виде для замкнутой СЭС записывается так (причем имеют место естественные ограничения Ф i t >0 и Ф c t >0)
Мы рассматриваем пока что социально-экономическую систему в предположении, что она не обменивается с окружающей средой ресурсами, финансами, информацией и т.п. Это, конечно, идеализация – однако она поможет нам провести классификацию состояний исследуемой системы. Фактически, речь сейчас идет о создании базовой модели, которая отражает основные черты и закономерности поведения системы. Впоследствии эту модель мы сможем дополнить – то есть изменить ее так, чтобы учесть интересующие нас эффекты – например, взаимодействие с окружением. Учет запрета на неограниченное возрастание значений Ф i t и Ф c t, а также учет однородности группы T= Z приводит к распределению знаков для (a i, aс), показанному на Рис. 6.4 (нетрудно показать, что любой иной простой случай спрямляем к этому типу - см., например, книги 1) Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия.- М.:Наука,1979.-760с. и 2) Рохлин В.А., Фукс Д.Б. Начальный курс топологии.-М.:Наука,1977.-488с.). В безразмерных переменных простейший выбор есть
Здесь b =Ti/Tc -безразмерный период малых колебаний вблизи точки 1 =(1,1), а Ti и Tc - характерные "времена нарастания" величин соответственно свободных и связанных финансов вблизи точки 1. Тогда орбиты являют собой винтовые линии в пространстве E, а пространство орбит E s взаимно - однозначно проектируется на плоскость (Ф c, Ф c) - см. Рис.6.4, где оно естественным образом разбивается на прямую сумму пространств
Таким образом, множество S состоит из двух элементов. Классификацию орбит можно произвести, например, по их минимальному значению на орбите: Ф i m =min (Ф i t) <1 (для нее одновременно Ф c m =min (Ф c t) <1), или же - по их периоду (то есть по минимальному времени Т такому, что Ф i t+Т=Ф i t и, соответственно, Ф i t+Т=Ф i t). Итак, в рамках самой простой модели взаимосвязи свободных и связанных финансов для замкнутой СЭС (то есть в отсутствие ее взаимодействия с окружением) могут реализоваться лишь два ее состояния, причем "типичным" является колебательное состояние. Таким образом, хотя данная модель и крайне огрублена, она тем не менее демонстрирует основные черты динамики макроэкономики СЭС, такие как "периодичность" (то есть - "экономические кризисы") и изменение характеристик состояния СЭС (амплитуды, периода колебаний) в результате как внутренней перестройки (когда "сдвигается" точка 1 - см. ниже), так и при внешних воздействиях (когда происходит перевод системы на иную орбиту - см. Рис.6.4). Необходимо также отметить, что учет социальных факторов приводит к выделению орбит с Ф i m <Ф i cr <1 (где Ф i cr - некое критическое значение Ф i), которые являются "социально опасными" в том смысле, что оставляют слишком малый резерв запаса свободных финансов для парирования внешних воздействий. Интересно, что данный подход позволяет выделить такие "опасные" орбиты еще далеко в "благоприятной области", когда Ф i t >>1 и (или) Фс t >>1, что дает время на принятие предупредительных мер. Данная модель легко обобщается на более сложные зависимости вторых слагаемых в правой части (6.8). Однако важность этой простой модели состоит в том, что она справедлива всегда для любой замкнутой макроэкономики в "опасной области" - то есть для орбит, далеких от "равновесной точки 1 (см. Рис.6.4) и поэтому представляет несомненный практический интерес. Поскольку на "каждом обороте" происходит "прибавление" финансов за счет вновь синтезированных, происходит своеобразная "раскрутка" системы - переход ее на "удаленные" орбиты. Настоящая модель дает возможность построить управление СЭС таким образом, чтобы удерживать ее все время в "неопасных" состояниях. Отметим, что связанные и свободные финансы в сумме не дают всей финансовой мощи государства: связанные финансы есть просто часть денег, которые вложены в новые (!) - лишь только в новые - технологии. Кроме того, в дальнейшем следует учесть наличие "разного времени оборачивается" - то есть того обстоятельства, что "разные задачи лежат на разных орбитах" (и имеют разные времена социализации). однако все это можно сделать в рамках развитого здесь подхода. Перейдем к рассмотрению незамкнутых СЭС. В общем случае внешнее воздействие на СЭС распадается на два предельных класса: когда t >>Т0 и когда t <<Т0, где t - характерное время внешнего воздействия, а Т0 - период для данной орбиты СЭС. Рассмотрим случай постоянных внешних воздействий - t >>Т0 (противоположный случай рассмотрен в следующем пункте). Перейдем также к непрерывным координатам, что позволит применять при исследовании методы качественной теории динамических систем на плоскости (см., например Баутин Н.Н., Леонтович Е.Л. Методы и приемы качественного исследования динамических систем на плоскости.-М.:Наука,1976.-496с.). Итак, уравнения (6.8) - (6.9) для открытой СЭС при постоянном внешнем воздействии примут вид
Особые точки получаются приравниванием к нулю правой части (4), и для них находим
Здесь обозначено b = d b. Чтобы проследить тенденцию, рассмотрим случай, когда ½ a ½, ½ b ½ <<1. Тогда в первом порядке
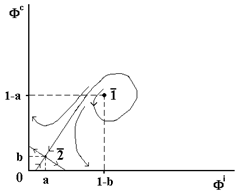
Исследование точек 1 и 2 свидетельствует о следующем: · при a>b точка 1 есть неустойчивый фокус, а 2 - седло; поведение фазовых траекторий (проекций орбит) показано на Рис. 6.5.
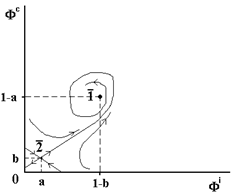
· при a<b точка 1 есть устойчивый фокус, а 2 - седло, см. Рис. 6.6.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.224.165 (0.013 с.) |

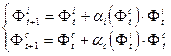 (6.8)
(6.8)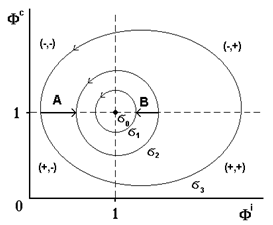
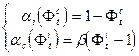 (6.9)
(6.9)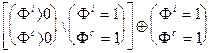 (6.10)
(6.10)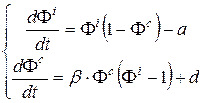 (6.11)
(6.11)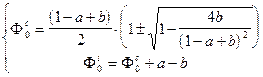 (6.12)
(6.12)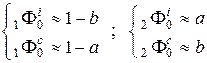 (6.13)
(6.13)