
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические погрешности оборудованияСодержание книги
Поиск на нашем сайте
Точность изготовления оборудования влияет на точность обрабатываемой детали. Показатели точности оборудования регламентированы стандартами и выявляются при их ненагруженном состоянии согласно стандартам, например, радиальное биение центрирующих поясков шпинделей токарных и фрезерных станков допускается до 0,01—0,015 мм, биение конического отверстия в шпинделях при проверке на оправке длиной 300 мм — 0,015— 0,02 мм, прямолинейность и параллельность направляющих токарных, продольно-строгальных и других станков на длине 1000 мм — 0,02 мм, параллельность осей шпинделей токарных станков направляющих станины на длине 300 мм в горизонтальной плоскости 0,01—0,015 мм, а в вертикальной плоскости — 0,02 мм и т.д. Из-за неточности оборудования появляются отклонения размеров, форм и пространственного положения обработанных по- верхностей от заданных, которые представляют собой систематические ошибки
где Продольная погрешность формы обточенной поверхности появляется в результате непрямолинейности направляющей станины в горизонтальной плоскости. Радиальное биение шпинделя приводит к образованию некруг- лости поверхности. При работе станка под нагрузкой показатели точности обработки изменяются, так как кроме геометрических неточностей станка появляются смещения узлов станка от действия сил резания. На практике почти не наблюдается случаев, когда возникает только одна какая-либо геометрическая погрешность оборудования. Обычно погрешности формы Геометрические погрешности возникают также из-за деформаций металлорежущих станков при их установке на фундаменты, а также из-за проседания фундаментов. В настоящее время начата разработка станков сверх особо высокой точности, которые относят к группам точности Т и К. Погрешности обработки на станках этих групп не должны превышать величины 0,3 мкм для группы Т и 0,1 мкм для группы К. ОПРЕДЕЛЕНИЕ СУММАРНОЙ ПОГРЕШНОСТИ МЕХАНИЧЕСКОЙ ОБРАБОТКИ В разделе 6.3 рассмотрены первичные погрешности механической обработки резанием и даны необходимые расчеты для определения числовых значений этих погрешностей. Однако главным является вопрос о нахождении суммарной погрешности обработки. Для определения ожидаемой точности необходимо суммировать первичные погрешности. Задачу о суммировании решают особо для каждого случая обработки и в зависимости от того, какую сущность в данном процессе имеет каждая погрешность. На ожидаемую точность влияют многие факторы, однако суммирование в большинстве случаев можно проводить по первичным погрешностям, рассмотренным выше. Рассмотрим вопрос суммирования при обработке заготовок на настроенных станках с использованием приспособлений. Предположим, что имеется такой случай обработки, когда каждая из первичных погрешностей представляет собой звено размерной цепи. Тогда ожидаемую точность Д можно представить как замыкающее звено цепи и суммирование первичных погрешностей производить алгебраически:
Задачу следует решать методом «максимума-минимума». При этом все первичные погрешности здесь отнесены к направлению выдерживаемого размера. Значение Расчет значения Возможен и другой метод расчета. Каждую первичную погрешность можно представить как вектор, модуль которого характеризует поле рассеивания погрешности или (что менее точно) разность предельных значений погрешности. Тогда значение
Этот метод лишь в исключительных случаях можно применять на практике, поскольку необходимо знать направление, в котором проявляется данная погрешность, что связано с трудностями в практической работе технолога. Каждый из предложенных выше методов суммирования имеет существенные недостатки, которые могут быть в значительной степени ослаблены, если первичные погрешности рассматривать как случайные величины. Такой подход вполне соответствует сути расчетно-статистического метода определения точности. Первые пять слагаемых в формуле (6.2) — случайные величины. Поэтому суммировать их необходимо по закону квадратного корня:
где р — коэффициент, определяющий процент риска получения брака при обработке; Риск возникает в связи с тем, что нельзя утверждать с полной определенностью, что рассеяние данной первичной погрешности соответствует данному закону распределения. При р = 1 вероятность брака составляет 32%, при р = 2 она снижается до 4,5%, а при р = 3 доходит до 0,27%. Коэффициенты Из практики известно, что
Величина
Последней формулой можно широко пользоваться на практике. Значения первичных погрешностей, суммируемых под знаком корня, представляют собой поле рассеяния этих величин. При обработке одной или нескольких заготовок используют метод пробных ходов и промеров. В этом случае ожидаемую погрешность рассчитывают по формуле:
где
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.68.115 (0.009 с.) |

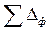 геометрического характера. Так, например, при обточке консольно закрепленной заготовки в результате непараллельности оси шпинделя направляющим станины в горизонтальной плоскости получается конусность:
геометрического характера. Так, например, при обточке консольно закрепленной заготовки в результате непараллельности оси шпинделя направляющим станины в горизонтальной плоскости получается конусность: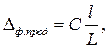
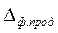 — отклонение формы обработанной поверхности в продольном сечении, мм; С — допускаемое отклонение от параллельности оси шпинделя направляющим станины в горизонтальной плоскости на длине L, мм; l — длина обрабатываемой поверхности, мм.
— отклонение формы обработанной поверхности в продольном сечении, мм; С — допускаемое отклонение от параллельности оси шпинделя направляющим станины в горизонтальной плоскости на длине L, мм; l — длина обрабатываемой поверхности, мм.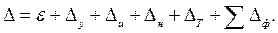 (6.2)
(6.2)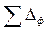 необходимо определять с учетом взаимной компенсации погрешностей технологической системы. При обработке тел вращения
необходимо определять с учетом взаимной компенсации погрешностей технологической системы. При обработке тел вращения 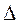 для диаметральных размеров нужно определять без учета
для диаметральных размеров нужно определять без учета 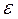 , равно как и для случая двухсторонней обработки элементов изделия набором режущих инструментов.
, равно как и для случая двухсторонней обработки элементов изделия набором режущих инструментов.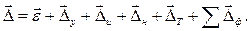 (6.3)
(6.3)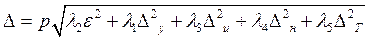 (6.4)
(6.4)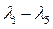 — коэффициенты, характеризующие законы распределения каждой из первичных погрешностей.
— коэффициенты, характеризующие законы распределения каждой из первичных погрешностей.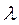 имеют вполне определенные значения для каждого закона распределения. Так, для закона нормального распределения
имеют вполне определенные значения для каждого закона распределения. Так, для закона нормального распределения 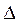 y,
y, 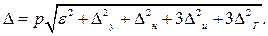 (6.5)
(6.5)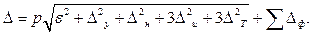 (6.6)
(6.6)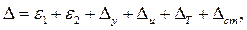 (6.7)
(6.7)


