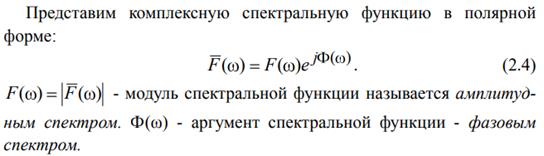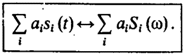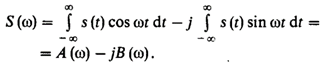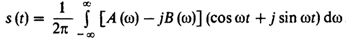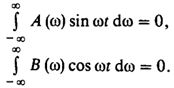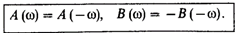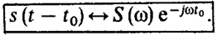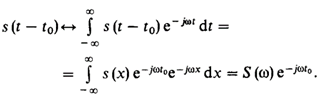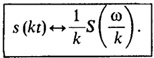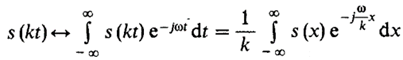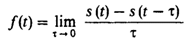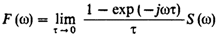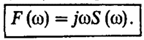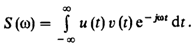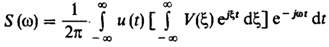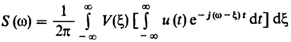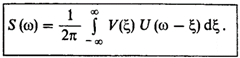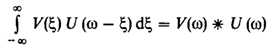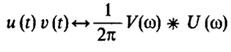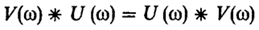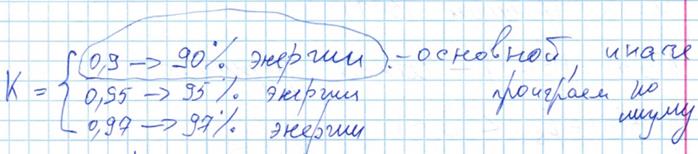Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение сигналов по базисным функциям. Понятие спектра сигнала. Представление сигналов в виде ряда Фурье.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пространством сигналов называется множество сигналов, обладающих общим свойством и отличающихся друг от друга, каким-либо параметром (расстоянием – речь же про векторы). Условия (аксиомы) линейного (оно же векторное) пространства М: · Любой сигнал · Для сигналов · Для любого · Множество В линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. Такая система линейно независимых векторов образует координатный базис в линейном пространстве. В разложении сигнала Разложение по базисным функциям: Фурье.
Ортонормированный базис Уолша. На отрезке своего существования
3,4…) Также можно упомянуть базисы: полиномы и функции Лежандра, Чебышева, Лагерра, Эрмита; мультипликативно-ортогональный базис. Разложение по ним есть в Лекции для КТ, с. 7.
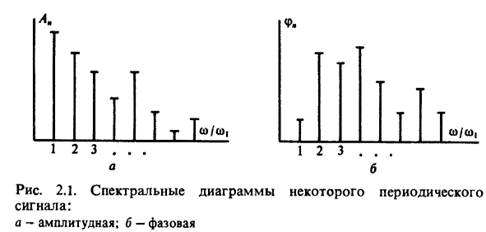
Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение сигнала.
Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:
Обобщенный ряд Фурье:
Сигнал u(t) может быть с определенной степенью точности представлен в виде набора ортогональных базисных функций Совокупность Рассмотрим спектральное представление периодического сигнала. Будем считать, что периодический сигнал определен на бесконечном интервале и может быть представлен в виде тригонометрического ряда Фурье (для периодического сигнала):
Коэффициенты Фурье:
Ряд Фурье можно записать также в комплексной форме[АП1]:
3. Прямое и обратное преобразования Фурье. Условия применимости. Физический смысл модуля и аргумента комплексной спектрально плотности S(jw) непериодического сигнала. Метод рядов Фурье допускает глубокое и плодотворное обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Среди последних для радиотехники наибольший интерес представляют импульсные сигналы. Для спектрального представления непериодических (импульсных) сигналов, заданных на интервале, непосредственно воспользоваться рядом Фурье и понятием спектра нельзя. Спектральные характеристики одиночных сигналов в этом случае определяются понятием спектральной плотности, для нахождения которой используется прямое преобразование Фурье, фактически вытекающее из ряда Фурье при бесконечном периоде повторения импульсных сигналов. Спектральную плотность также называют спектральной функцией или Фурье-образом сигнала.
Обратное преобразование Фурье позволяет найти сигнал s(t) по известной спектральной плотности:
Спектральная плотность определена выше только для абсолютно интегрируемых сигналов, т. е. сигналов, удовлетворяющих условию:
Такое условие существенно сужает класс сигналов, для которых существует Физический смысл спектральной плотности – спектральная плотность есть коэффициент пропорциональности между длиной малого интервала частот ∆f и отвечающей ему комплексной амплитудой ∆Af0 гармонического сигнала с частотой f0. (https://kpfu.ru/staff_files/F1700343876/SPEKTRY_02.01.15.pdf)
Если на оси частот взять некоторую последовательность равноотстоящих точек 0<w1<w2…, то модуль спектральной плотности установит линейный масштаб вдоль кривых: чем больше модуль спектральной плотности в заданной области частот, тем реже будут располагаться частотные точки на векторной диаграмме. 4. Связь между спектральной плотностью S(jw) одиночного импульса и спектром периодического сигнала. Важнейшие свойства преобразования Фурье и их практическое использование.
(Баскаков, с. 51. Аналогичный материал можно дополнительно почитать в первой лекции Сювы по спектрам) Удобная табличка со свойствами преобразования Фурье:
Для русскоговорящих: shift – смещение, derivative – производная, convolution – свертка. Ниже то же самое подробней. · Линейность преобразования Фурье (важнейшее) Если имеется некоторая совокупность сигналов s1(t), s2(t),…, причем s1(t) эквивалентно S1(w) и так по парам, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:
Здесь ai – произвольные числовые коэффициенты. · Свойства вещественной и мнимой частей спектральной плотности. Пусть сигнал s(t) – сигнал, принимающий вещественные значения. Его спектральная плотность в общем случае является комплексной:
Подставим выражение в формулу обратного преобразования Фурье:
Чтобы сигнал, полученный путем такого двукратного преобразования, оставался вещественным, необходимо потребовать, чтобы
Это возможно лишь в том случае, если вещественная часть A(w) спектральной плотности сигнала есть четная, а мнимая часть B(w) – нечетная функция частоты:
· Спектральная плотность сигнала, смещенного во времени. Предположим, что для s(t) известно эквивалентное соответствие s(t) ↔ S(w). Рассмотрим такой же сигнал, но возникающий на t0 секунд позднее. Принимая точку t0 за новое начало отсчета времени, обозначим этот смещенный сигнал как s(t-t0). Покажем, что
· Зависимость спектральной плотности сигнала от выбора масштаба измерения времени. Предположим, что исходный сигнал s(t) подвергнут изменению масштаба времени. Это означает, что роль времени t играет новая независимая переменная kt. Если k > 1 – «сжатие» исходного сигнала, если 0 < k < 1 – «растяжение». Если s(t) ↔ S(w):
· Спектральная плотность производной и неопределенного интеграла. Пусть сигнал s(t) и его спектральная плотность S(w) заданы. Будем изучать новый сигнал f(t)=ds/dt и поставим цель найти его спектральную плотность F(w). По определению:
Преобразование Фурье – линейная операция, значит равенство справедливо и по отношению к спектральным плотностям. Учитывая выражение из «Спектральная плотность сигнала, смещенного во времени»:
Представляя экспоненциальную функцию рядом Тейлора: exp(-jwt) = 1 - jwt - (wt)2/2 - …, подставляя этот ряд в выражение выше и ограничиваясь первыми двумя членами находим:
jw – оператор дифференцирования в частотной области, 1/jw – оператор интегрирования в частотной области. · Спектральная плотность сигнала на выходе интегратора (свертка по времени) Интегратор – физическая система, выходной сигнал которой пропорционален интегралу от входного воздействия. · Спектральная плотность произведения сигналов (свертка по частоте). При суммировании сигналов их спектры складываются, однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей. Пусть u(t) и v(t) – два сигнала, для которых известны соответствия u(t) ↔ U(w), v(t) ↔ V(w). Произведение сигналов s(t) = u(t)*v(t). Спектральная плотность:
Обратное преобразование Фурье, выражаем v(t) через его спектральную плотность и подставим в S(w):
Меняем порядок интегрирования:
Откуда:
Интеграл в правой части – свертка функций V и U. Символически означается так:
Таким образом спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свертке спектральных плотностей сомножителей:
Операция свертки коммутативна:
5. Понятие ширины спектра сигнала и методы его определения. Практическое использование ширины спектра сигналов (перепишите плес из лекций, что Стася кидала. Там прям с языка Есипы снято). (https://kpfu.ru/staff_files/F1700343876/SPEKTRY_02.01.15.pdf) Ширина спектра является одним из важнейших числовых параметров сигнала. Физически реализуемый сигнал всегда имеет конечную протяженность во времени. Его спектр теоретически занимает частоты от нуля до бесконечности. Однако практика показывает, а теория обосновывает, что для удовлетворительного описания сигнала достаточно учесть спектр в конечном интервале частот fн < f < fв. Поэтому шириной спектра сигнала называется интервал частот f = fв – fн, в котором содержится наибольшая часть энергии (мощности) сигнала. Частоты fн - нижняя и fв - верхняя граничные частоты интервала соответственно. Для оценки ширины спектра используется амплитудный спектр, так как он определяет энергию (4.6) и среднюю мощность (4.3) сигнала, однако до сих пор нет единого критерия для этой оценки. Но для любого критерия, используемого на практике, доля энергии (мощности) сигнала, которая содержится в ∆f, составляет не менее 90% от всей энергии (мощности) сигнала.
(Lektsii_Esipenko_RTsS.pdf)
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 1019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

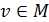 при любых t принимает лишь вещественные значения
при любых t принимает лишь вещественные значения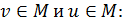 коммутативность (
коммутативность (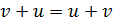 ), ассоциативность
), ассоциативность 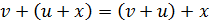
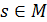 и любого вещественного
и любого вещественного 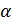 определен сигнал
определен сигнал 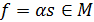
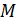 содержит нулевой элемент
содержит нулевой элемент 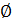 , такой, что
, такой, что 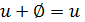 для всех
для всех 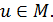
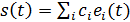 , где
, где 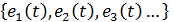 -- линейно независимые векторы (базис),
-- линейно независимые векторы (базис), 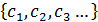 -- проекции
-- проекции 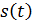 относительно этого базиса.
относительно этого базиса.

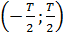 функции Уолша принимают только значения
функции Уолша принимают только значения 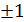 .
.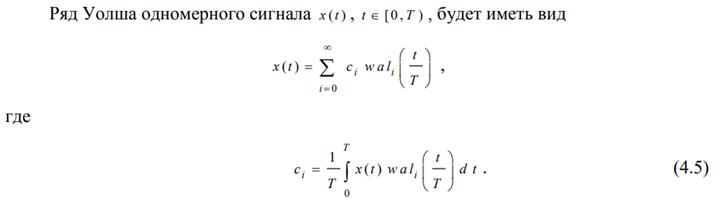
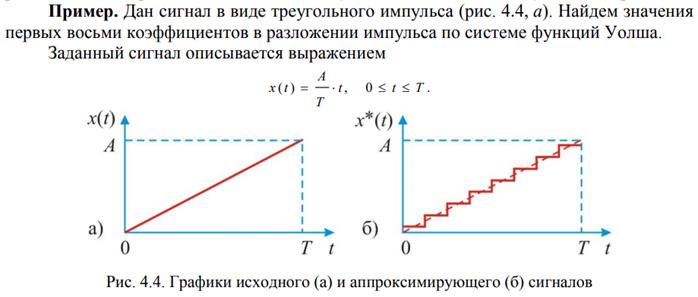

 Спектр сигнала — коэффициенты разложения сигнала в базисе ортогональных функций.
Спектр сигнала — коэффициенты разложения сигнала в базисе ортогональных функций.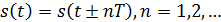
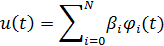
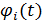 , взятых с весовыми коэффициентами
, взятых с весовыми коэффициентами 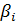 . Для базисных функций скалярное произведение (
. Для базисных функций скалярное произведение (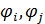 )=0 при i=j.
)=0 при i=j.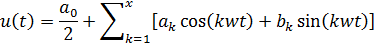
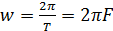 – частота основной гармоники сигнала, kw – высшие гармоники.
– частота основной гармоники сигнала, kw – высшие гармоники.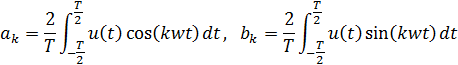
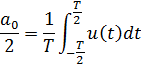
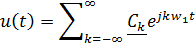
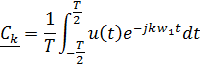
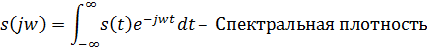
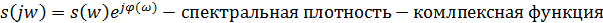
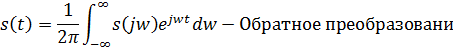
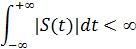
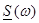 . В этом смысле нельзя говорить о спектральной плотности гармонического сигнала S(t)=Umcosω0t, если на него не наложено условие ограниченности во времени.
. В этом смысле нельзя говорить о спектральной плотности гармонического сигнала S(t)=Umcosω0t, если на него не наложено условие ограниченности во времени.