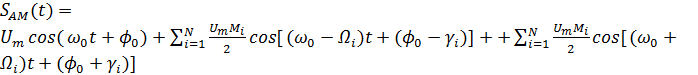Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Амплитудная модуляция и спектр ам колебания при модуляции гармоническим колебанием и произвольным сигналом. Векторная диаграмма ам колебания.Содержание книги
Поиск на нашем сайте
(Баскаков, с. 92) (Лекции для КТ) Физический процесс управления параметрами несущего колебания называется модуляцией. Запишем несущее гармоническое колебание в виде
где Um, ω0 и φ0 соответственно амплитуда, несущая частота и начальная фаза колебания. Если пропорционально информационному сигналу S(t) изменяется амплитуда Um сигнала, такой сигнал называется сигналом с амплитудной модуляцией, а если – мгновенная частота ω, то имеет место сигнал с частотной модуляцией (ЧМ), ω = ω(t). Если пропорционально информационному сигналу S(t) изменяется полная фаза θ(t), такой сигнал называется сигналом с фазовой модуляцией или ФМ сигналом. Математическая модель выглядит так:
где Um – амплитуда сигнала при отсутствии модуляции, k – коэффициент пропорциональности,
Пусть Тогда Величина Таким образом, в данном случае:
При M≤1 имеет место неискаженная модуляция. При этом:
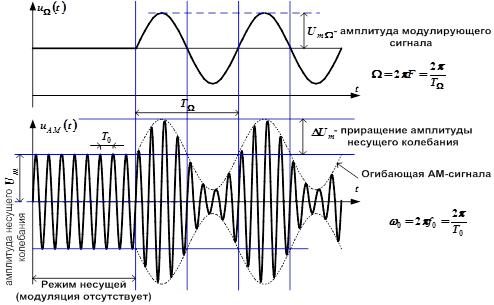
Отсюда можно получить, что Осциллограммы имеют вид
Рис.6. Формирование сигнала с амплитудной модуляцией Основные свойства АМ-сигнала достаточно четко видны из рассмотрения случая однотональной модуляции (т.е. модуляции гармоническим колебанием частоты Ω). Раскроем предыдущие выражения для АМ-сигнала:
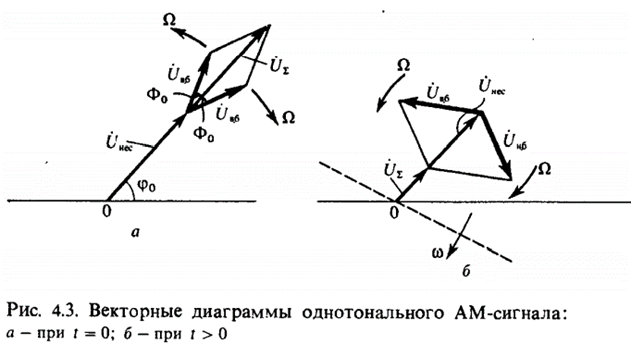
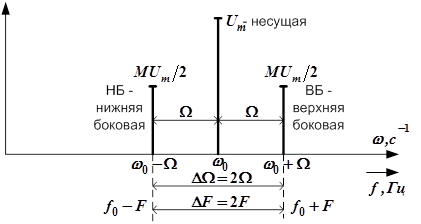
Свойства: 1) помимо несущего колебания в спектре есть ещё две гармонические составляющие, 2) их уровень зависит от М, и при М=1 их амплитуда максимальна и в 2 раза меньше амплитуды несущего колебания, 3) эти составляющие расположены симметрично справа и слева относительно ω0, 4) при γ=0 фазы боковых составляющих совпадают с фазой несущего колебания. При γ≠0 они симметричны относительно фазы несущего колебания.
Рис.7. Спектр сигнала с гармонической амплитудной модуляцией
АМ-модуляция сложным сигналом При сложном 0 е имеем:
Здесь Мi – парциальный индекс модуляции. Тогда спектр АМ-сигнала можно представить так:
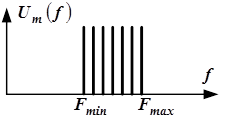
Рис.9. Спектр информационного сигнала
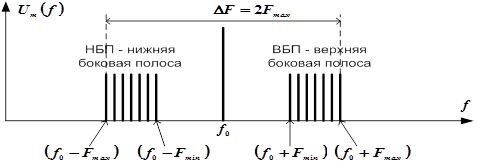
Рис.10. Спектр АМ-сигнала при модуляции сложным сигналом Ширина спектра АМ-сигнала равна удвоенному значению максимальной частоты в спектре модулирующего сигнала.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |

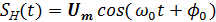
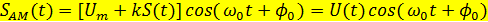
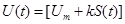 – связь между амплитудой несущего колебания и информационным сигналом S(t): приращение огибающей пропорционально S(t),
– связь между амплитудой несущего колебания и информационным сигналом S(t): приращение огибающей пропорционально S(t),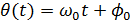 – полная фаза колебания или мгновенная фаза.
– полная фаза колебания или мгновенная фаза.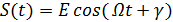 , где E, Ω, и γ – амплитуда, частота и фаза информационного сигнала.
, где E, Ω, и γ – амплитуда, частота и фаза информационного сигнала.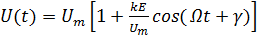
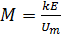 есть коэффициент амплитудной модуляции.
есть коэффициент амплитудной модуляции.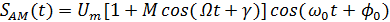
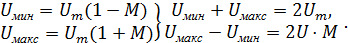
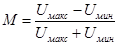 .
.
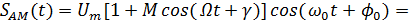
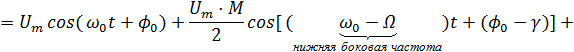
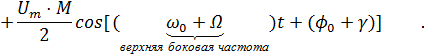
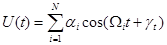 – его представление в виде ряда Фурье или при наличии другой совокупности гармонических колебаний. При этом:
– его представление в виде ряда Фурье или при наличии другой совокупности гармонических колебаний. При этом: