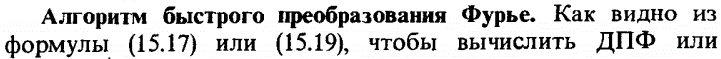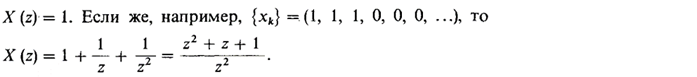Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация радиотехнических сигналов. Виды и модели сигналов. Основные параметры сигналов.Содержание книги
Поиск на нашем сайте
Шпора на экзамен по дисциплине: «Радиотехнические цепи и сигналы»
Выполнили: Студенты группы 18-ТР
г. Нижний Новгород 2020 Использовать на свой страх и риск. Перед применением проконсультируйтесь с преподавателем. Полезные ссылки 1. Баскаков в PDF – https://1drv.ms/b/s!AtbJDClZE1KXgdgjDyApZweO4-BEhg?e=dzrMNq 2. Ответы на экзаменационные вопросы.docx – https://1drv.ms/w/s!AtbJDClZE1KXgd5VvbvxFq2bYybheg?e=yYeuzA 3. Lektsii_Esipenko_RTsS.pdf – https://1drv.ms/b/s!AtbJDClZE1KXg_E307nWNuBcgpVrLw?e=dvmMlj
Оглавление Полезные ссылки. 2 1. Классификация радиотехнических сигналов. Виды и модели сигналов. Основные параметры сигналов. 6 2. Разложение сигналов по базисным функциям. Понятие спектра сигнала. Представление сигналов в виде ряда Фурье. 9 3. Прямое и обратное преобразования Фурье. Условия применимости. Физический смысл модуля и аргумента комплексной спектрально плотности S(jw) непериодического сигнала. 13 4. Связь между спектральной плотностью S(jw) одиночного импульса и спектром периодического сигнала. Важнейшие свойства преобразования Фурье и их практическое использование. 15 5. Понятие ширины спектра сигнала и методы его определения. Практическое использование ширины спектра сигналов (перепишите плес из лекций, что Стася кидала. Там прям с языка Есипы снято). 20 6. Автокорреляционная функция (АКФ) детерминированного сигнала, ее свойства и практическое использование. Ее связь со спектральной плотностью сигнала. 22 7. Случайные процессы и их происхождение. Основные характеристики случайных процессов. 25 8. Основные свойства плотности вероятности и функции распределения случайных величин. Методы и примеры определения числовых характеристик случайных процессов. 28 9. Понятие стационарности и эргодичности случайных процессов. Практическое использование этих понятий при определении характеристик случайных процессов. 31 10. Корреляционные функции случайного процесса. Методы их нахождения для стационарных и эргодических процессов. 33 11. Гауссовский (нормальный) случайный процесс и его характеристики, центральная предельная теорема. 34 12. Спектральные характеристики случайного процесса. Теорема Винера-Хинчина. 36 13. Эффективная ширина спектра и интервал корреляции случайного процесса. Связь между ними. 40
14. Белый шум: корреляционная функция и спектральная плотность мощности. Прохождение белого шума через линейную цепь. 42 15. Основные характеристики линейной стационарной цепи во временной и в частотной областях. Их взаимосвязь. 47 16. Связь между детерминированными сигналами на входе и выходе линейной цепи по временной и частотной областях. 52 17. Связь между энергетическими спектрами сигналов на входе и выходе линейной цепи. Нормализация случайного процесса линейной цепью. 55 18. Узкополосный случайный процесс. Плотность вероятности огибающей и мгновенной фазы. 57 19. Назначение и виды модуляции сигналов. Выбор частоты несущего колебания. 62 20. Амплитудная модуляция и спектр АМ колебания при модуляции гармоническим колебанием и произвольным сигналом. Векторная диаграмма АМ колебания. 64 21. Общее выражение для колебания с угловой модуляцией. Спектр ЧМ и ФМ сигналов. 69 22. Физический смысл девиации частоты и индексов частотной и угловой модуляции. Связь между мгновенной частотой и мгновенной фазой колебания. 72 23. Практическая ширина полосы частот спектра ЧМ и ФМ колебаний. Отличия спектров при ЧМ и ФМ модуляции. 74 24. Нелинейные цепи, классификация. Методы аппроксимации характеристик нелинейных элементов и условия их применимости. 77 25. Методы анализа воздействия гармонического колебания на нелинейный элемент. 82 26. Воздействие суммы гармонических колебаний на нелинейный элемент. Спектральные характеристики сигналов при бигармоническом воздействии. 87 27. Кусочно-линейная аппроксимация ВАХ НЭ. Анализ спектра на выходе НЭ с использованием коэффициентов Берга. 90 28. Схема типового радиотехнического звена с нелинейным преобразованием сигналов, назначение элементов. Типовые устройства. Преобразователи частоты. 93 29. Схема и процесс получения сигналов с амплитудной модуляцией. Получение однополосной модуляции. 102 30. Методы детектирования сигналов с амплитудной модуляцией: линейное и квадратичное. 105 31. Методы и схемы получения сигналов с угловой модуляцией. 107 32. Обратная связь в линейной системе. Коэффициент передачи системы с обратной связью. Положительная и отрицательная обратная связь. 109
33. Влияние обратной связи на характеристики системы. Общие условия и критерии устойчивости линейной цепи с обратной связью. 112 34. LC-автогенераторы с трансформаторной обратной связью. Условие возбуждения и перехода в стационарный режим. 116 35. Режим мягкого и жёсткого возбуждения автогенератора. 118 36. Преобразователи аналоговых сигналов в цифровой вид. 120 37. Дискретизация сигналов, теорема Котельникова и базис Котельникова. 123 38. Спектры дискретизированных сигналов. Условия восстановления непрерывного сигнала по дискретным отсчетам. 126 39. Методы анализа дискретных сигналов и цепей. 131 40. Дискретное и быстрое преобразование Фурье. 135 41. Z-преобразование и его свойства. 141 42. Дискретные фильтры. Разностное уравнение, системная функция и импульсная характеристика цифрового (дискретного) фильтра. 143 43. Типы и формы реализации дискретных (цифровых) фильтров. 151 44. Структуры и сравнение КИХ- и БИХ-фильтров. 155 45. Частотные характеристики цифровых фильтров. 158 46. Методы синтеза цифровых фильтров по аналоговому прототипу. 160 47. Преимущества и недостатки цифровой обработки сигналов. 164
Классификация · · o Сигнал, описываемый одной функцией времени – одномерный o Многомерный сигнал – упорядоченная совокупность одномерных сигналов (пример – система напряжений на зажимах многополюсника)
· o o Случайный сигнал – в радиотехнике часто проявляют себя как помехи
Импульсные сигналы
Видеоимпульсы представляют собой кратковременные односторонние (относительно оси времени) изменения напряжения или тока в цепи постоянного тока, а радиоимпульсы — сигнал, состоящий из высокочастотных колебаний напряжения или тока, огибающая которых повторяет форму видеоимпульса. В импульсной технике в основном рассматривают видеоимпульсы.
· o Аналоговый сигнал – значения сигнала можно измерять в любые моменты времени. Пример – осцилограмма физического процесса; o Дискретный сигнал – является прерывистым (в отличие от аналогового), принимает значения только в определенные моменты времени. Простейшая мат. модель – счетное количество точек ti, в каждой из которых определено значение si. Шаг дискретизации ∆ = ti+1 – ti для каждого сигнала постоянен.
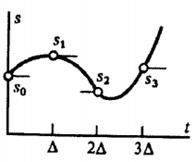
o Цифровые сигналы – отсчетные значения представлены в формате чисел. Модели сигналов Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. При устремлении длительности элементарных сигналов к нулю точность представления исходного сигнала возрастает. Такое представление называется динамическим представлением сигналов.
представление функциями а) Хевисайда (step function); б) Дирака (delta function)
а)
Динамическое предсавление:
б)
Динамическое представление:
Основные параметры сигналов
Условие нормировки Условие симметрии:
4) условие согласованности
Совместный центральный момент второго порядка двух случайных величин служит мерой статистической связи этих случайных величин и называется корреляционной функцией:
Если в этом выражении mi и mj не вычитать (опустить, т.е. использовать не центрированные случайные величины), то такая функция называется ковариационной:
В западной литературе и в некоторых наших источниках эти функции принято менять на противоположные (корреляционная функция называется ковариационной, а ковариационная – корреляционной). Применение в теории случайных процессов известной пары преобразований Фурье позволяет ввести понятие спектральной плотности мощности стационарного случайного процесса (спектра мощности):
W(ω) – чётная функция частоты (как и R(τ)). Тогда мы приходим к наиболее употребительным формулам:
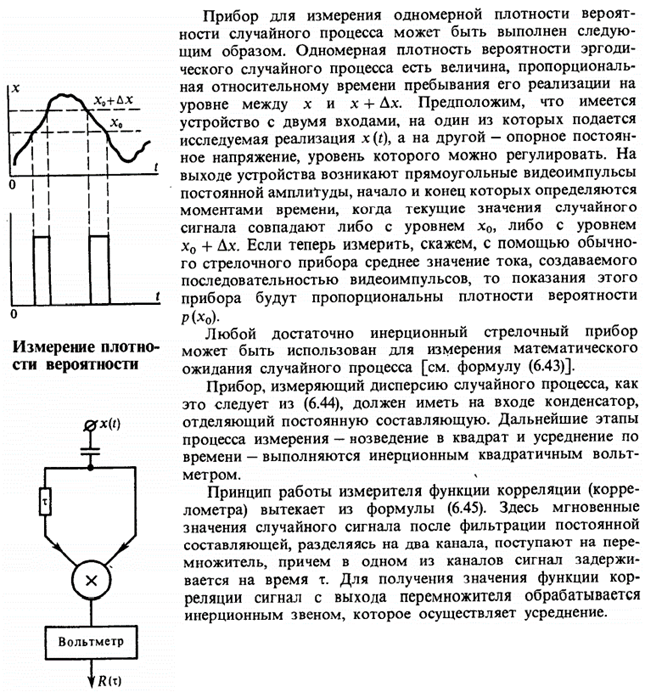
F(ω) и N(f) – односторонние спектры мощности случайного процесса. 8. Основные свойства плотности вероятности и функции распределения случайных величин. Методы и примеры определения числовых характеристик случайных процессов. (Баскаков, с. 144) (также см. прошлый вопрос – свойства плотности вероятности и функции распределения выделены жирным)
(Баскаков, с. 160)
Фазовая модуляция (ФМ) При данном виде модуляции пропорционально сообщению S(t) изменяется полная фаза θ(t) несущего колебания:
где Если сообщение S(t) есть гармоническое колебание, т.е.
где При этом математическая модель сигнала с фазовой модуляцией имеет вид
Для мгновенной частоты этого сигнала имеем:
где Таким образом, при фазовой модуляции изменяется также мгновенная частота. Частотная модуляция (ЧМ) При данном виде модуляции пропорционально сообщению S(t) изменяется мгновенная частота:
Если
где Для полной фазы имеем
где
Математическая модель сигнала с частотной модуляцией имеет вид:
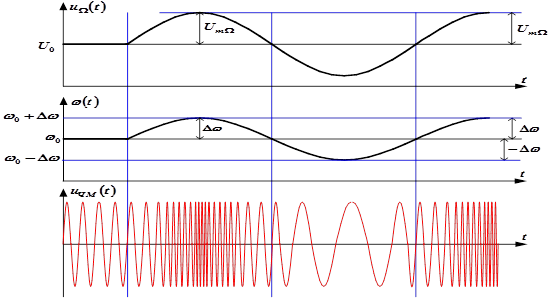
Различие сигналов с фазовой и частотной модуляциями проявляется только при модуляции сложным сообщением (смотри приведённые ниже рисунки).
Рис.17 – Качественное поведение параметров сигналов при фазовой и частотной модуляциях
Осциллограмма сигнала с ЧМ имеет вид
Рис.18 – Осциллограмма сигнала с ЧМ
Спектры сигналов с угловой модуляцией
Полагаем
Следует иметь в виду 2 случая. 1. βУМ << 1. В этом случае справедливы соотношения: Тогда
В спектре – те же частоты, что и при АМ-колебании. Ширина спектра та же, что и у АМ-сигнала и равна
2. βУМ >> 1. При этом справедливы следующие разложения:
Тогда имеем следующее:
где Jn(o) – функция Бесселя порядка n. Ширина спектра:
Замечание: сигналы с угловой модуляцией получили достаточно широкое распространение, т.к. в условиях действия помех дают возможность передать сообщения по каналу связи с более высокой достоверностью, чем при АМ. (Баскаков, с. 100) Базис Котельникова
Спектральный анализ · Хотелось бы посмотреть на спектр сигнала, но как его отобразить? Применим алгоритм: o Возьмем нужный нам отрезок длины 2 m (отрезок меньшей длины можно дополнить нулями) o Если необходимо как-то улучшить изображение спектра, получаемое на выходе, то умножим сигнал на весовое окно o Вычислим FFT имеющегося сигнала o Переведем полученные коэффициенты в полярную форму, чтобы получить их амплитуды и фазы o Получим график зависимости амплитуды от частоты (Дальше в презентации идут непонятные слова, о которых Есипа спрашивать скорее всего не будет, вроде вейвлетов и преобразования Хаара) Фильтрация: · Методы проектирования фильтров: o Построение фильтра с линейной фазой по произвольной заданной частотной характеристике o Частотная характеристика приближается к заданной с любым заданным уровнем точност · Спектры сигналов при фильтрации (свертке) перемножаются · Фильтры бывают идеальные (модельные) и используемые на практике Шумоподавление: · Аддитивный шум – такой шум, когда сигнал можно представить в виде:
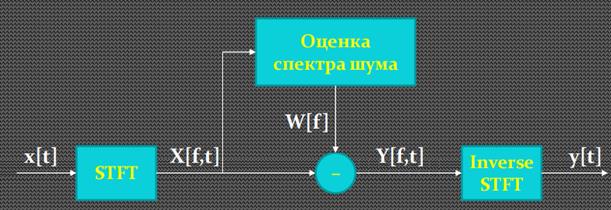
· Схема алгоритма спектрального вычитания:
40. Дискретное и быстрое преобразование Фурье (Баскаков, с. 388)
(На с. 391 можно найти про восстановление сигнала по ДПФ и больше про обратное ДПФ. Там же про геометрическую трактовку)
· Быстрое преобразование Фурье (FFT) – ускорение вычисления ДПФ · Основной принцип - периодичность базисных функций => много одинаковых множителей, которые можно каждый раз не вычислять · Основные преимущества: o Математическая точность (ошибки округления меньше, т.к. меньше число операций) o Число умножений порядка N·log2N, намного меньше, чем N2 при достаточно больших N
41. Z-преобразование и его свойства. (Баскаков, с. 396)
(Про сходимость ряда, преобразование непрерывных функций, обратное преобразование и прочее можно прочитать на с. 397)
Разностное уравнение
Системная функция
Импульсная характеристика
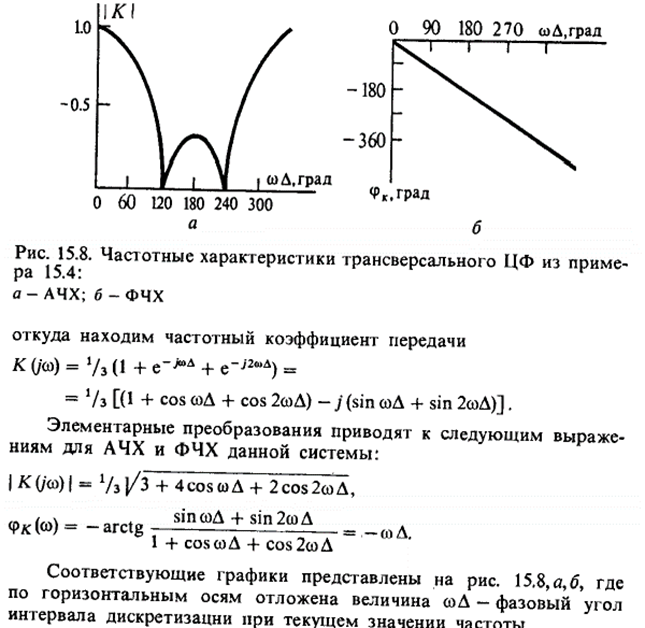
Для трансверсального:
(А вот для рекурсивного про частотные характеристики отдельно почему-то нет, но можно глянуть сравнение в предыдущем вопросе)
Шпора на экзамен по дисциплине: «Радиотехнические цепи и сигналы»
Выполнили: Студенты группы 18-ТР
г. Нижний Новгород 2020 Использовать на свой страх и риск. Перед применением проконсультируйтесь с преподавателем. Полезные ссылки 1. Баскаков в PDF – https://1drv.ms/b/s!AtbJDClZE1KXgdgjDyApZweO4-BEhg?e=dzrMNq 2. Ответы на экзаменационные вопросы.docx – https://1drv.ms/w/s!AtbJDClZE1KXgd5VvbvxFq2bYybheg?e=yYeuzA 3. Lektsii_Esipenko_RTsS.pdf – https://1drv.ms/b/s!AtbJDClZE1KXg_E307nWNuBcgpVrLw?e=dvmMlj
Оглавление Полезные ссылки. 2 1. Классификация радиотехнических сигналов. Виды и модели сигналов. Основные параметры сигналов. 6 2. Разложение сигналов по базисным функциям. Понятие спектра сигнала. Представление сигналов в виде ряда Фурье. 9 3. Прямое и обратное преобразования Фурье. Условия применимости. Физический смысл модуля и аргумента комплексной спектрально плотности S(jw) непериодического сигнала. 13 4. Связь между спектральной плотностью S(jw) одиночного импульса и спектром периодического сигнала. Важнейшие свойства преобразования Фурье и их практическое использование. 15 5. Понятие ширины спектра сигнала и методы его определения. Практическое использование ширины спектра сигналов (перепишите плес из лекций, что Стася кидала. Там прям с языка Есипы снято). 20 6. Автокорреляционная функция (АКФ) детерминированного сигнала, ее свойства и практическое использование. Ее связь со спектральной плотностью сигнала. 22 7. Случайные процессы и их происхождение. Основные характеристики случайных процессов. 25 8. Основные свойства плотности вероятности и функции распределения случайных величин. Методы и примеры определения числовых характеристик случайных процессов. 28 9. Понятие стационарности и эргодичности случайных процессов. Практическое использование этих понятий при определении характеристик случайных процессов. 31 10. Корреляционные функции случайного процесса. Методы их нахождения для стационарных и эргодических процессов. 33 11. Гауссовский (нормальный) случайный процесс и его характеристики, центральная предельная теорема. 34 12. Спектральные характеристики случайного процесса. Теорема Винера-Хинчина. 36 13. Эффективная ширина спектра и интервал корреляции случайного процесса. Связь между ними. 40 14. Белый шум: корреляционная функция и спектральная плотность мощности. Прохождение белого шума через линейную цепь. 42 15. Основные характеристики линейной стационарной цепи во временной и в частотной областях. Их взаимосвязь. 47 16. Связь между детерминированными сигналами на входе и выходе линейной цепи по временной и частотной областях. 52 17. Связь между энергетическими спектрами сигналов на входе и выходе линейной цепи. Нормализация случайного процесса линейной цепью. 55 18. Узкополосный случайный процесс. Плотность вероятности огибающей и мгновенной фазы. 57 19. Назначение и виды модуляции сигналов. Выбор частоты несущего колебания. 62 20. Амплитудная модуляция и спектр АМ колебания при модуляции гармоническим колебанием и произвольным сигналом. Векторная диаграмма АМ колебания. 64 21. Общее выражение для колебания с угловой модуляцией. Спектр ЧМ и ФМ сигналов. 69 22. Физический смысл девиации частоты и индексов частотной и угловой модуляции. Связь между мгновенной частотой и мгновенной фазой колебания. 72 23. Практическая ширина полосы частот спектра ЧМ и ФМ колебаний. Отличия спектров при ЧМ и ФМ модуляции. 74 24. Нелинейные цепи, классификация. Методы аппроксимации характеристик нелинейных элементов и условия их применимости. 77 25. Методы анализа воздействия гармонического колебания на нелинейный элемент. 82 26. Воздействие суммы гармонических колебаний на нелинейный элемент. Спектральные характеристики сигналов при бигармоническом воздействии. 87 27. Кусочно-линейная аппроксимация ВАХ НЭ. Анализ спектра на выходе НЭ с использованием коэффициентов Берга. 90 28. Схема типового радиотехнического звена с нелинейным преобразованием сигналов, назначение элементов. Типовые устройства. Преобразователи частоты. 93 29. Схема и процесс получения сигналов с амплитудной модуляцией. Получение однополосной модуляции. 102 30. Методы детектирования сигналов с амплитудной модуляцией: линейное и квадратичное. 105 31. Методы и схемы получения сигналов с угловой модуляцией. 107 32. Обратная связь в линейной системе. Коэффициент передачи системы с обратной связью. Положительная и отрицательная обратная связь. 109 33. Влияние обратной связи на характеристики системы. Общие условия и критерии устойчивости линейной цепи с обратной связью. 112 34. LC-автогенераторы с трансформаторной обратной связью. Условие возбуждения и перехода в стационарный режим. 116 35. Режим мягкого и жёсткого возбуждения автогенератора. 118 36. Преобразователи аналоговых сигналов в цифровой вид. 120 37. Дискретизация сигналов, теорема Котельникова и базис Котельникова. 123 38. Спектры дискретизированных сигналов. Условия восстановления непрерывного сигнала по дискретным отсчетам. 126 39. Методы анализа дискретных сигналов и цепей. 131 40. Дискретное и быстрое преобразование Фурье. 135 41. Z-преобразование и его свойства. 141 42. Дискретные фильтры. Разностное уравнение, системная функция и импульсная характеристика цифрового (дискретного) фильтра. 143 43. Типы и формы реализации дискретных (цифровых) фильтров. 151 44. Структуры и сравнение КИХ- и БИХ-фильтров. 155 45. Частотные характеристики цифровых фильтров. 158 46. Методы синтеза цифровых фильтров по аналоговому прототипу. 160 47. Преимущества и недостатки цифровой обработки сигналов. 164
Классификация радиотехнических сигналов. Виды и модели сигналов. Основные параметры сигналов. Классификация · · o Сигнал, описываемый одной функцией времени – одномерный o Многомерный сигнал – упорядоченная совокупность одномерных сигналов (пример – система напряжений на зажимах многополюсника)
· o o Случайный сигнал – в радиотехнике часто проявляют себя как помехи
Импульсные сигналы
Видеоимпульсы представляют собой кратковременные односторонние (относительно оси времени) изменения напряжения или тока в цепи постоянного тока, а радиоимпульсы — сигнал, состоящий из высокочастотных колебаний напряжения или тока, огибающая которых повторяет форму видеоимпульса. В импульсной технике в основном рассматривают видеоимпульсы.
· o Аналоговый сигнал – значения сигнала можно измерять в любые моменты времени. Пример – осцилограмма физического процесса; o Дискретный сигнал – является прерывистым (в отличие от аналогового), принимает значения только в определенные моменты времени. Простейшая мат. модель – счетное количество точек ti, в каждой из которых определено значение si. Шаг дискретизации ∆ = ti+1 – ti для каждого сигнала постоянен.
o Цифровые сигналы – отсчетные значения представлены в формате чисел. Модели сигналов Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. При устремлении длительности элементарных сигналов к нулю точность представления исходного сигнала возрастает. Такое представление называется динамическим представлением сигналов.
представление функциями а) Хевисайда (step function); б) Дирака (delta function)
а)
Динамическое предсавление:
б)
Динамическое представление:
Основные параметры сигналов
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.016 с.) |

 Вещественные и комплексные сигналы (по виду функции, описывающей сигнал);
Вещественные и комплексные сигналы (по виду функции, описывающей сигнал); Одномерные и многомерные сигналы
Одномерные и многомерные сигналы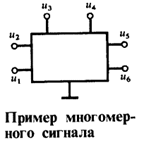

 Детерминированные и случайные сигналы (по возможности предсказания мгновенного значения в опр. момент времени)
Детерминированные и случайные сигналы (по возможности предсказания мгновенного значения в опр. момент времени) Детерминированный – если можно предсказать значение (в природе не существует, идеализация);
Детерминированный – если можно предсказать значение (в природе не существует, идеализация);
 Импульсы – колебания в пределах конечного отрезка времени. Различают видеоимпульсы и радиоимпульсы. Если uв(t) – видеоимпульс, то соответствующий ему радиоимпульс uр(t) = uв(t)cos(w0t+j0).
Импульсы – колебания в пределах конечного отрезка времени. Различают видеоимпульсы и радиоимпульсы. Если uв(t) – видеоимпульс, то соответствующий ему радиоимпульс uр(t) = uв(t)cos(w0t+j0).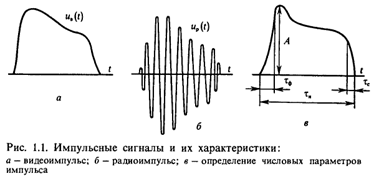
 Аналоговые, дискретные и цифровые сигналы.
Аналоговые, дискретные и цифровые сигналы.
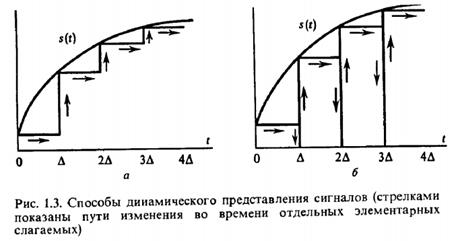
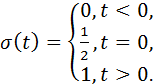
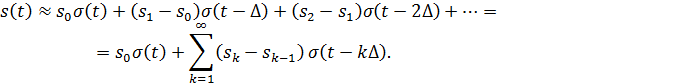
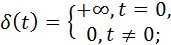
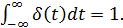
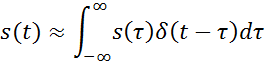
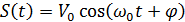
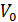 – амплитуда,
– амплитуда,
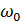 – частота,
– частота,
 – фаза сигнала.
– фаза сигнала.
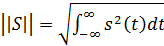 – норма.
– норма.
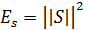 – энергия сигнала.
– энергия сигнала.
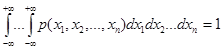 ,
,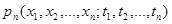 не изменяется при произвольной перестановке своих аргументов:
не изменяется при произвольной перестановке своих аргументов: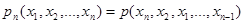 ,
,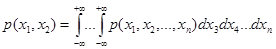 .
.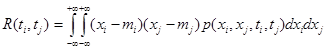 .
.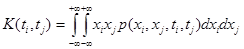 .
.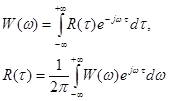 – пара преобразования Винера-Хинчина.
– пара преобразования Винера-Хинчина.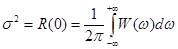 .
.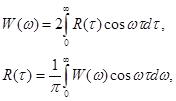
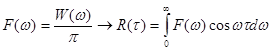 ,
,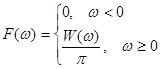 ,
,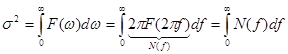 .
.












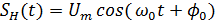 ,
, 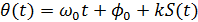 ,
,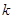 – коэффициент пропорциональности.
– коэффициент пропорциональности.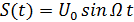 , то
, то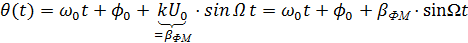 ,
,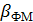 – коэффициент или индекс фазовой модуляции.
– коэффициент или индекс фазовой модуляции.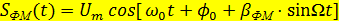 .
.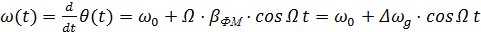 ,
,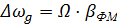 – девиация или максимальное отклонение мгновенной частоты сигнала от ω0.
– девиация или максимальное отклонение мгновенной частоты сигнала от ω0.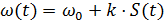 .
.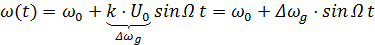 ,
,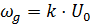 – девиация частоты.
– девиация частоты.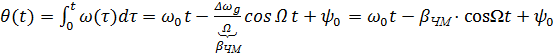 ,
,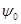 – постоянная интегрирования,
– постоянная интегрирования,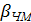 – коэффициент или индекс частотной модуляции.
– коэффициент или индекс частотной модуляции.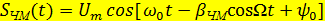 .
.
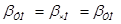 , φ0 и ψ0 с целью упрощения опускаем. Тогда:
, φ0 и ψ0 с целью упрощения опускаем. Тогда: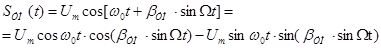 .
.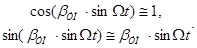
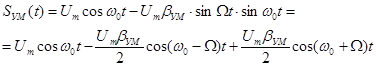 .
.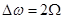 .
.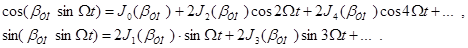
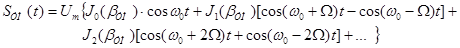 ,
,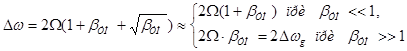 .
.


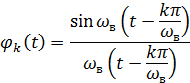

















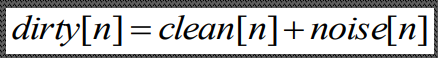



 [АП10]
[АП10]