
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие стационарности и эргодичности случайных процессов. Практическое использование этих понятий при определении характеристик случайных процессов.Содержание книги
Поиск на нашем сайте
(Баскаков, с. 157)
(Баскаков, с. 158)
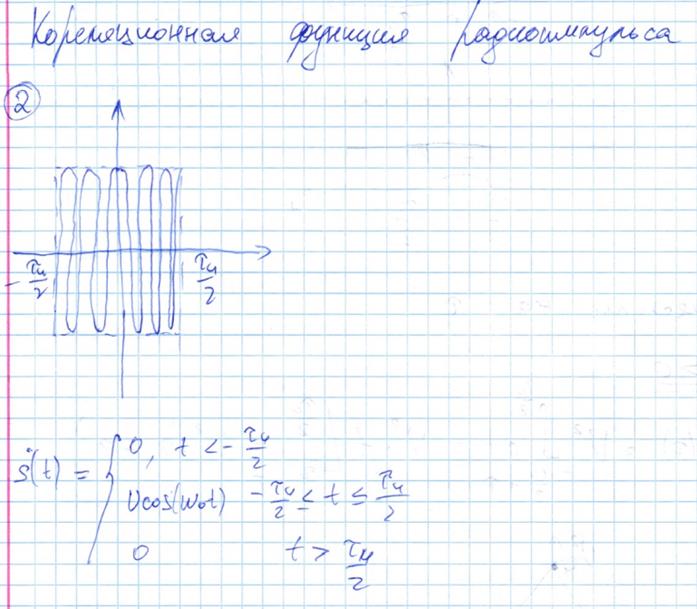
Корреляционные функции случайного процесса. Методы их нахождения для стационарных и эргодических процессов. (Lektsii_Esipenko_RTsS.pdf)
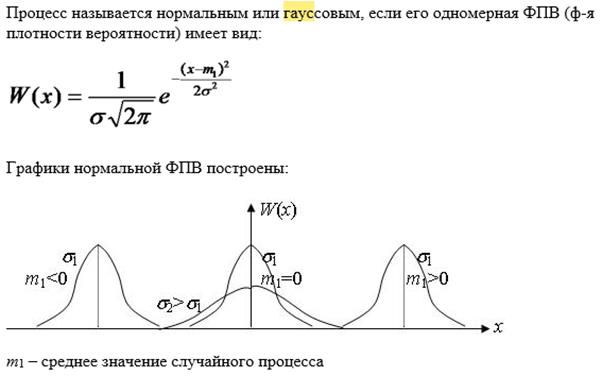
(Больше там по этому поводу ничего нет…) Гауссовский (нормальный) случайный процесс и его характеристики, центральная предельная теорема (https://ru.wikipedia.org/wiki/Гауссовский_процесс)
Характеристики: m1 – математическое ожидание, {\displaystyle \sigma }
(https://ru.wikipedia.org/wiki/Центральная_предельная_теорема) Центральные предельные теоремы (ЦПТ)
Центральные предельные теоремы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.
Спектральные характеристики случайного процесса. Теорема Винера-Хинчина. (Баскаков, с. 164)
Эффективная ширина спектра и интервал корреляции случайного процесса. Связь между ними. (Баскаков, с. 169)
(https://siblec.ru/radiotekhnika-i-elektronika/radiotekhnicheskie-tsepi-i-signaly/5-sluchajnye-signaly/5-5-effektivnaya-shirina-spektra-i-interval-korrelyatsii) Произведение эффективной ширины спектра и интервала корреляции представляет собой постоянную величину. Из этого вытекает, что чем шире энергетический спектр, тем меньше интервал корреляции между его значениями и наоборот. Но ширина энергетического спектра определяет скорость изменения значений случайного процесса: чем больше Белый шум: корреляционная функция и спектральная плотность мощности. Прохождение белого шума через линейную цепь. (Баскаков, с. 170)
(https://elar.urfu.ru/bitstream/10995/66712/1/978-5-7996-2567-2_2019.pdf)
15. Основные характеристики линейной стационарной цепи во временной и в частотной областях. Их взаимосвязь[АП2]. (Баскаков, с. 191)
(Баскаков, с. 194)
Связь между детерминированными сигналами на входе и выходе линейной цепи по временной и частотной областях. (Док Влада) (также см. предыдущий вопрос)
(Баскаков, с. 209)
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.009 с.) |




































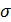 — среднеквадратическое отклонение (
— среднеквадратическое отклонение (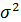 {\displaystyle \sigma ^{2}}
{\displaystyle \sigma ^{2}}  — дисперсия) распределения.
— дисперсия) распределения.
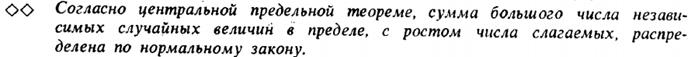






































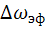 (или чем меньше
(или чем меньше 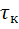 ), тем выше скорость изменения процесса.
), тем выше скорость изменения процесса.

















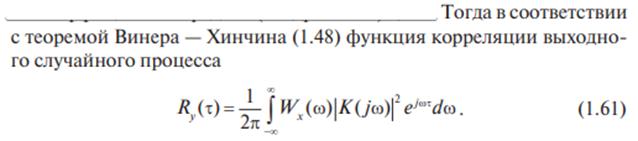
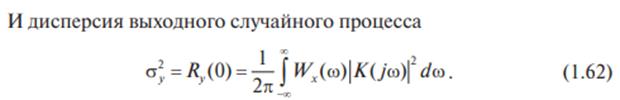











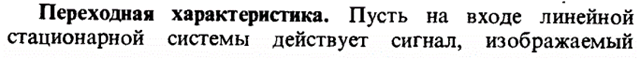




 [АП3]
[АП3]
























