Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные фильтры. Разностное уравнение, системная функция и импульсная характеристика цифрового (дискретного) фильтра.Содержание книги
Поиск на нашем сайте (Вопрос 39) · Методы проектирования фильтров: o Построение фильтра с линейной фазой по произвольной заданной частотной характеристике o Частотная характеристика приближается к заданной с любым заданным уровнем точност · Спектры сигналов при фильтрации (свертке) перемножаются · Фильтры бывают идеальные (модельные) и используемые на практике (Баскаков, с. 400)
Разностное уравнение
Системная функция
Импульсная характеристика
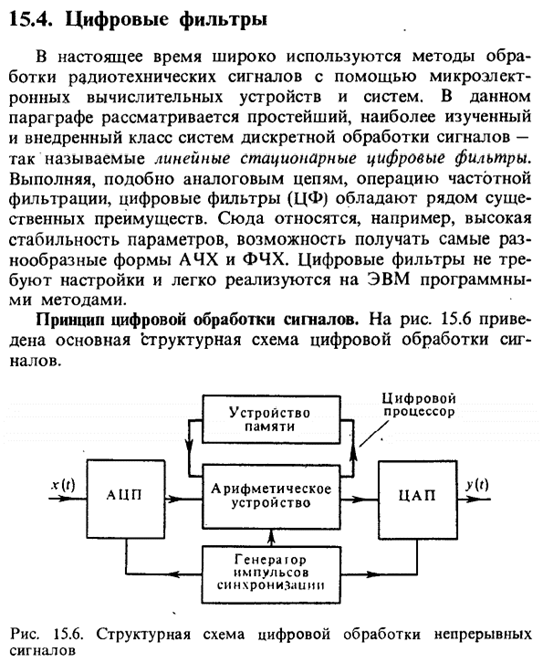
Типы и формы реализации дискретных (цифровых) фильтров. (Баскаков, с. 405)
(Схему можно найти в следующем вопросе)
(Полная рекурсня…)
(Схему также ищем в следующем вопросе)
(Про устройчивость можно почитать на с. 410, не уверен, что оно тут нужно)
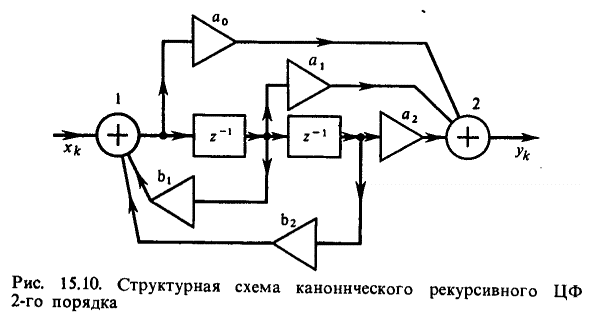
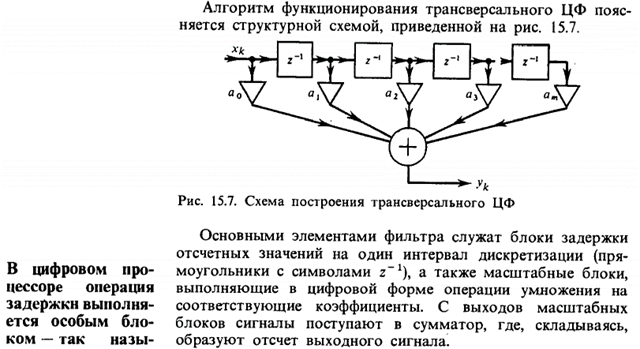
Структуры и сравнение КИХ- и БИХ-фильтров (https://ru.wikipedia.org/wiki/Фильтр_с_конечной_импульсной_характеристикой) Фильтр с конечной импульсной характеристикой (Нерекурсивный фильтр, КИХ-фильтр, трансверсальный ЦФ) или FIR-фильтр (FIR сокр. от finite impulse response — конечная импульсная характеристика) — один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — константа. (Баскаков, с. 406)
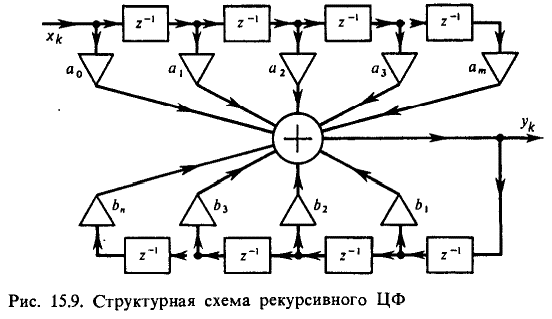
(https://ru.wikipedia.org/wiki/Фильтр_с_бесконечной_импульсной_характеристикой) Фильтр с бесконечной импульсной характеристикой (Рекурсивный фильтр, БИХ-фильтр) или IIR-фильтр (IIR сокр. от infinite impulse response — бесконечная импульсная характеристика) — линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образующий обратную связь. Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми, так и цифровыми. (Баскаков, с. 409)
(Баскаков, с. 409)
(Баскаков, с. 415)
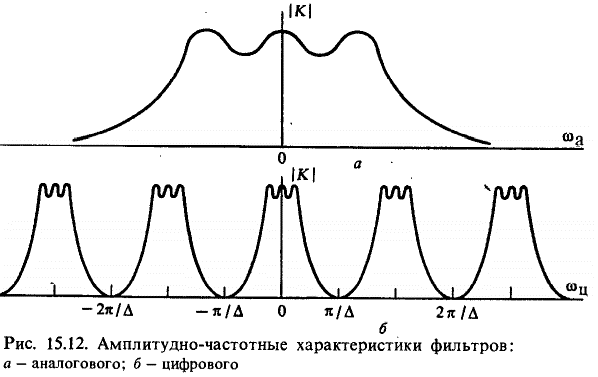
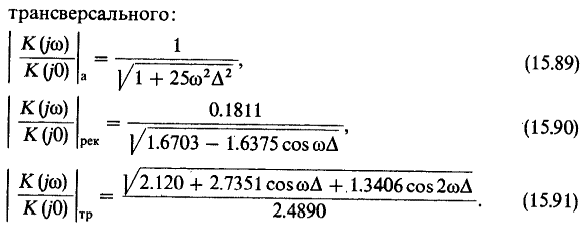
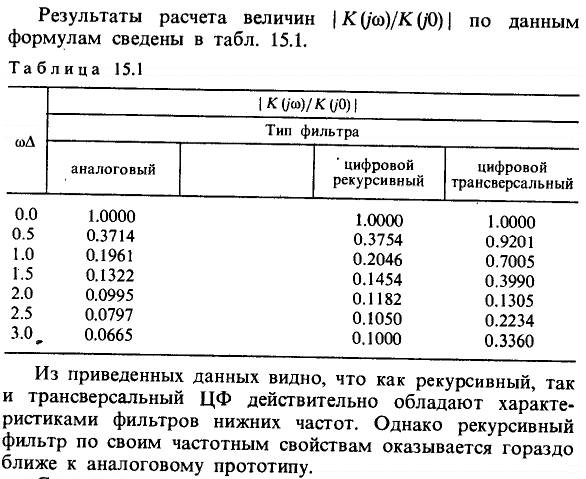
Частотные характеристики цифровых фильтров (Также см. пару предыдущих вопросов)
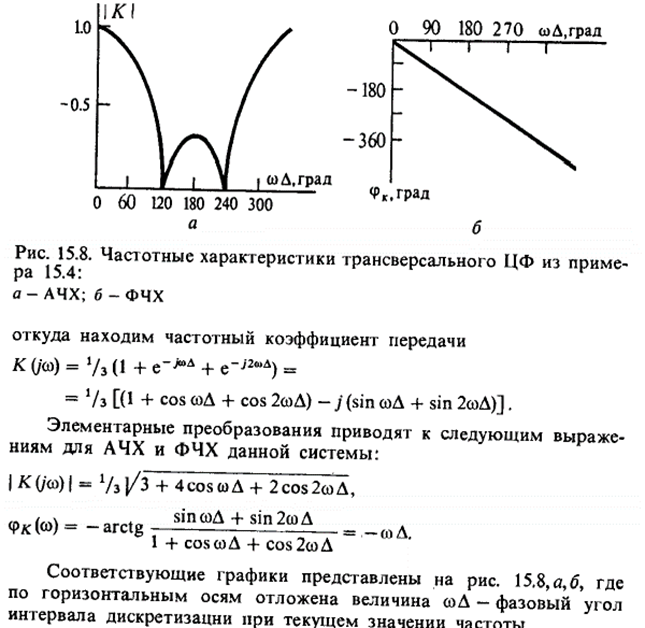
Для трансверсального:
(А вот для рекурсивного про частотные характеристики отдельно почему-то нет, но можно глянуть сравнение в предыдущем вопросе)
Методы синтеза цифровых фильтров по аналоговому прототипу. (Баскаков, с. 414)
(Про влияние квантования сигнала читаем на с. 419, если надо)
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |








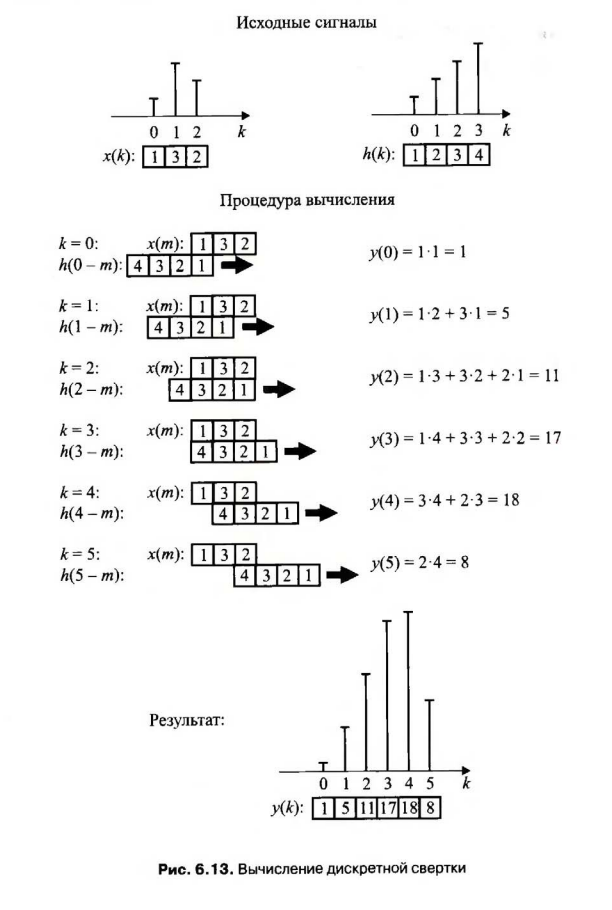




























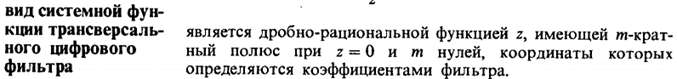










 (Баскаков, с. 406)
(Баскаков, с. 406)






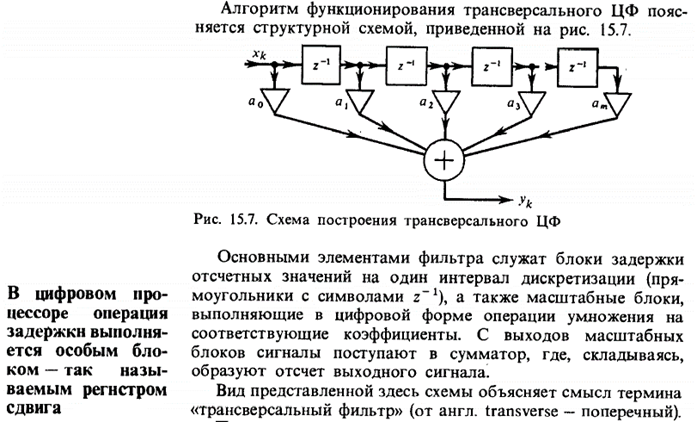




 (Баскаков, с. 407)
(Баскаков, с. 407)