Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляционная функция (акф) детерминированного сигнала, ее свойства и практическое использование. Ее связь со спектральной плотностью сигнала.Содержание книги
Поиск на нашем сайте
(Баскаков, с. 78)
· Для работы импульсных радиолокаторов · Для изучения пространственного распределения галактик · Для узкого рассеивания рентгеновских лучей (изучение наноструктур)
Случайные процессы и их происхождение. Основные характеристики случайных процессов. (Баскаков, с. 155) (Лекции для КТ.doc, с. 25) Случайным процессом называют некоторую случайную функцию, зависящую от текущего аргумента, чаще всего – времени, мгновенные значения которой в любые моменты времени сами являются случайными величинами. Бесконечный ансамбль случайных величин также можно назвать случайным процессом. Наиболее часто случайный процесс принято определять множеством
1. функция распределения 2. плотность распределения вероятностей p(x1, x2,… xn, t1, t2,… tn), 3. энергетический спектр
Она определяется так:
Её свойства: 1)
Плотность распределения вероятностей Она определяется через и удовлетворяет условию:
Очевидно, что
В приведённых соотношениях опущены аргументы времени для упрощения. Свойства плотности распределения вероятностей: 1) условие положительной определённости: Условие нормировки Условие симметрии:
4) условие согласованности
Совместный центральный момент второго порядка двух случайных величин служит мерой статистической связи этих случайных величин и называется корреляционной функцией:
Если в этом выражении mi и mj не вычитать (опустить, т.е. использовать не центрированные случайные величины), то такая функция называется ковариационной:
В западной литературе и в некоторых наших источниках эти функции принято менять на противоположные (корреляционная функция называется ковариационной, а ковариационная – корреляционной). Применение в теории случайных процессов известной пары преобразований Фурье позволяет ввести понятие спектральной плотности мощности стационарного случайного процесса (спектра мощности):
W(ω) – чётная функция частоты (как и R(τ)). Тогда мы приходим к наиболее употребительным формулам:
F(ω) и N(f) – односторонние спектры мощности случайного процесса. 8. Основные свойства плотности вероятности и функции распределения случайных величин. Методы и примеры определения числовых характеристик случайных процессов. (Баскаков, с. 144) (также см. прошлый вопрос – свойства плотности вероятности и функции распределения выделены жирным)
(Баскаков, с. 160)
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.011 с.) |




















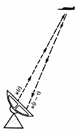 Применение
Применение



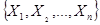 .
.




 Наиболее важными характеристиками являются:
Наиболее важными характеристиками являются: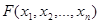 ,
,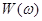 .
. Функция распределения
Функция распределения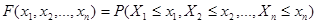 .
.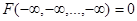 , 2)
, 2) 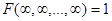 .
.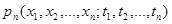
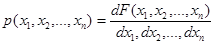 ,
,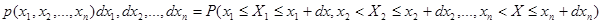 .
.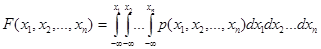 .
.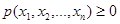 ,
,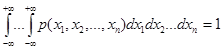 ,
,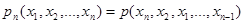 ,
,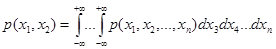 .
.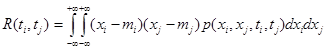 .
.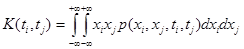 .
.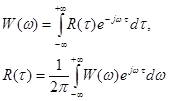 – пара преобразования Винера-Хинчина.
– пара преобразования Винера-Хинчина.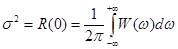 .
.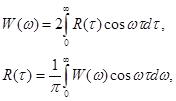
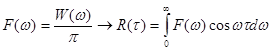 ,
,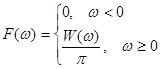 ,
,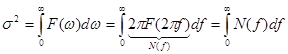 .
.