Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее выражение для колебания с угловой модуляцией. Спектр ЧМ и фм сигналов.Содержание книги
Поиск на нашем сайте
(Лекции для КТ) Фазовая и частотная модуляции имеют общее название "угловая модуляция". Все основные свойства сигналов с угловой модуляцией достаточно четко видны при гармоническом сообщении. При этом оба вида модуляции неразличимы. Фазовая модуляция (ФМ) При данном виде модуляции пропорционально сообщению S(t) изменяется полная фаза θ(t) несущего колебания:
где Если сообщение S(t) есть гармоническое колебание, т.е.
где При этом математическая модель сигнала с фазовой модуляцией имеет вид
Для мгновенной частоты этого сигнала имеем:
где Таким образом, при фазовой модуляции изменяется также мгновенная частота. Частотная модуляция (ЧМ) При данном виде модуляции пропорционально сообщению S(t) изменяется мгновенная частота:
Если
где Для полной фазы имеем
где
Математическая модель сигнала с частотной модуляцией имеет вид:
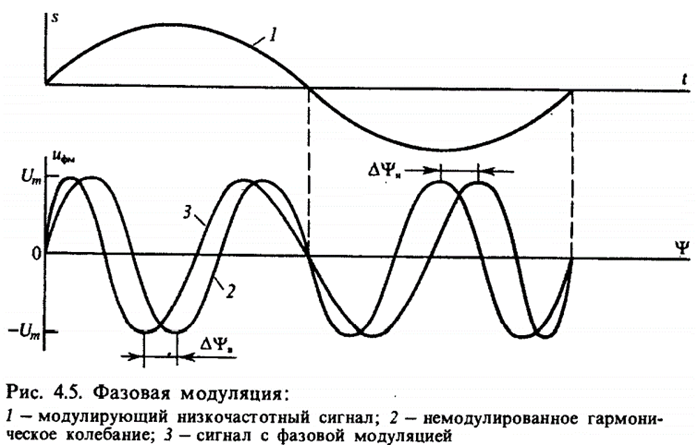
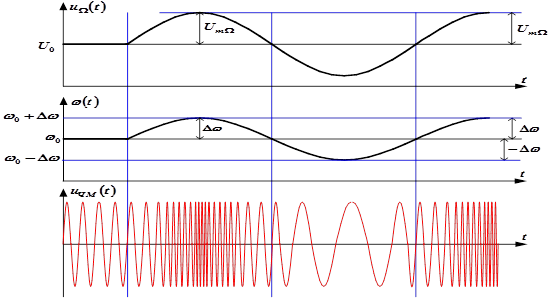
Различие сигналов с фазовой и частотной модуляциями проявляется только при модуляции сложным сообщением (смотри приведённые ниже рисунки).
Рис.17 – Качественное поведение параметров сигналов при фазовой и частотной модуляциях
Осциллограмма сигнала с ЧМ имеет вид
Рис.18 – Осциллограмма сигнала с ЧМ
Спектры сигналов с угловой модуляцией
Полагаем
Следует иметь в виду 2 случая. 1. βУМ << 1. В этом случае справедливы соотношения: Тогда
В спектре – те же частоты, что и при АМ-колебании. Ширина спектра та же, что и у АМ-сигнала и равна
2. βУМ >> 1. При этом справедливы следующие разложения:
Тогда имеем следующее:
где Jn(o) – функция Бесселя порядка n. Ширина спектра:
Замечание: сигналы с угловой модуляцией получили достаточно широкое распространение, т.к. в условиях действия помех дают возможность передать сообщения по каналу связи с более высокой достоверностью, чем при АМ.
(Баскаков, с. 100) Физический смысл девиации частоты и индексов частотной и угловой модуляции. Связь между мгновенной частотой и мгновенной фазой колебания. (Баскаков, с. 101)
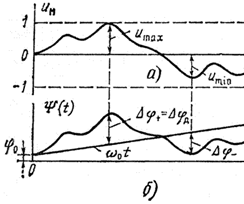
Физический смысл этого коэффициента поясняется на рисунке, где изображены модулирующий сигнал и полная фаза ФМ сигнала.
С увеличением сигнала полная фаза растет во времени быстрее, чем по линейному закону.
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.91.173 (0.009 с.) |

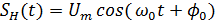 ,
, 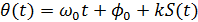 ,
,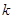 – коэффициент пропорциональности.
– коэффициент пропорциональности.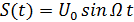 , то
, то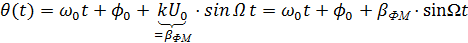 ,
,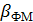 – коэффициент или индекс фазовой модуляции.
– коэффициент или индекс фазовой модуляции.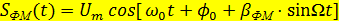 .
.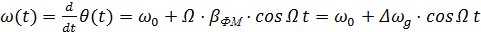 ,
,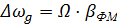 – девиация или максимальное отклонение мгновенной частоты сигнала от ω0.
– девиация или максимальное отклонение мгновенной частоты сигнала от ω0.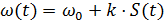 .
.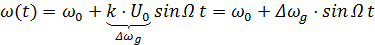 ,
,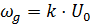 – девиация частоты.
– девиация частоты.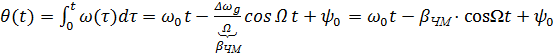 ,
,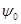 – постоянная интегрирования,
– постоянная интегрирования,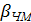 – коэффициент или индекс частотной модуляции.
– коэффициент или индекс частотной модуляции.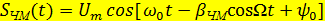 .
.
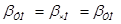 , φ0 и ψ0 с целью упрощения опускаем. Тогда:
, φ0 и ψ0 с целью упрощения опускаем. Тогда: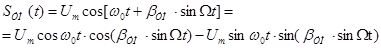 .
.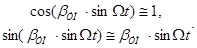
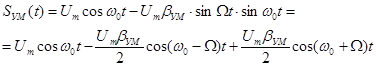 .
.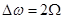 .
.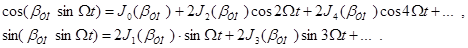
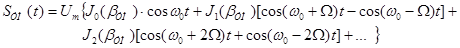 ,
,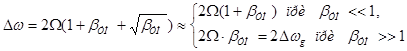 .
.