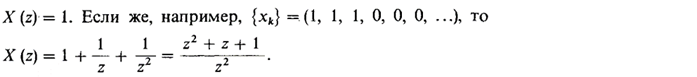Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы анализа дискретных сигналов и цепей.Содержание книги
Поиск на нашем сайте
(http://www.machinelearning.ru/wiki/images/3/3a/Signals_Ryzhkov.pdf) (как я понимаю – обзорный вопрос по всем приемам с дискретными сигналами, рассмотренными ранее и далее) Дискретизация сигнала: (Подробнее смотри в вопросах выше) Дискретизацию аналогового сигнала S = x(t) можно проводить двумя способами: · Дискретизация по частоте (по аргументу t) · Дискретизация по амплитуде (по значению функции S)
· Введем понятие спектра аналогового сигнала:
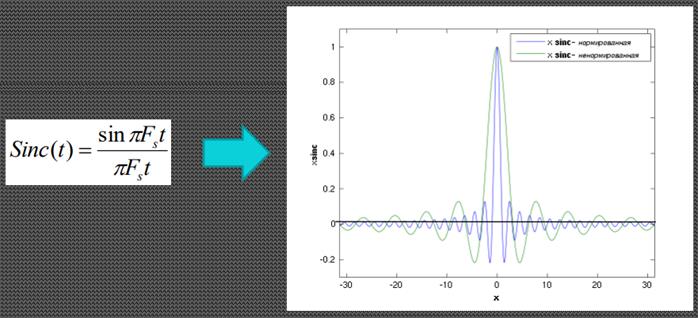
· Здесь x(t) – исходный сигнал, X(v) – спектр сигнала (коэффициенты при гармониках с частотой v) · То есть мы раскладываем сигнал на синусы и косинусы с различными частотами Теорема Котельникова: (Подробнее смотри в вопросах выше) · Спектр сигнала x(t) не содержит частот выше F, т.е. · X(v) = 0 за пределами отрезка [-F, F] · Дискретизация сигнала x(t) производится с частотой Fs, т.е. в моменты времени nT, где T= Fs-1 · Fs > 2F Тогда исходный аналоговый сигнал x(t) можно точно восстановить из его цифровых отсчетов x(nT), пользуясь интерполяционной формулой
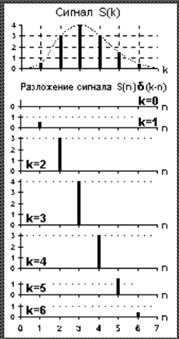
Импульсная характеристика: · Единичный импульс δ(n) · Разложение произвольного сигнала на сумму единичных импульсов
· Отклик системы на единичный импульс δ(n) называется импульсной характеристикой или импульсным откликом системы Преобразование Фурье: (Подробнее в следующем вопросе) · Преобразование Фурье – разложение исходного сигнала на различные синусоиды · Дискретное преобразование Фурье
· Если исходный сигнал – вещественный, то формула записывается в следующем виде:
· Преобразование Фурье обратимо, то есть существуют прямое и обратное преобразования Фурье · Прямое преобразование Фурье – умножение отсчетов исходного сигнала на соответствующие синусы и косинусы Спектральный анализ · Хотелось бы посмотреть на спектр сигнала, но как его отобразить? Применим алгоритм: o Возьмем нужный нам отрезок длины 2 m (отрезок меньшей длины можно дополнить нулями) o Если необходимо как-то улучшить изображение спектра, получаемое на выходе, то умножим сигнал на весовое окно o Вычислим FFT имеющегося сигнала o Переведем полученные коэффициенты в полярную форму, чтобы получить их амплитуды и фазы o Получим график зависимости амплитуды от частоты (Дальше в презентации идут непонятные слова, о которых Есипа спрашивать скорее всего не будет, вроде вейвлетов и преобразования Хаара)
Фильтрация: · Методы проектирования фильтров: o Построение фильтра с линейной фазой по произвольной заданной частотной характеристике o Частотная характеристика приближается к заданной с любым заданным уровнем точност · Спектры сигналов при фильтрации (свертке) перемножаются · Фильтры бывают идеальные (модельные) и используемые на практике Шумоподавление: · Аддитивный шум – такой шум, когда сигнал можно представить в виде:
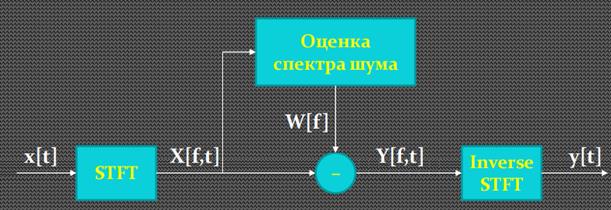
· Схема алгоритма спектрального вычитания:
40. Дискретное и быстрое преобразование Фурье (Баскаков, с. 388)
(На с. 391 можно найти про восстановление сигнала по ДПФ и больше про обратное ДПФ. Там же про геометрическую трактовку)
· Быстрое преобразование Фурье (FFT) – ускорение вычисления ДПФ · Основной принцип - периодичность базисных функций => много одинаковых множителей, которые можно каждый раз не вычислять · Основные преимущества: o Математическая точность (ошибки округления меньше, т.к. меньше число операций) o Число умножений порядка N·log2N, намного меньше, чем N2 при достаточно больших N
41. Z-преобразование и его свойства. (Баскаков, с. 396)
(Про сходимость ряда, преобразование непрерывных функций, обратное преобразование и прочее можно прочитать на с. 397)
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.01 с.) |


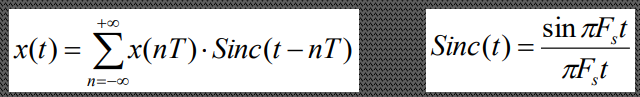
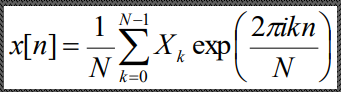
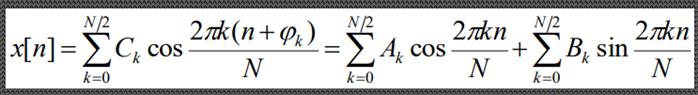
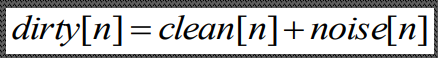



 [АП10]
[АП10]