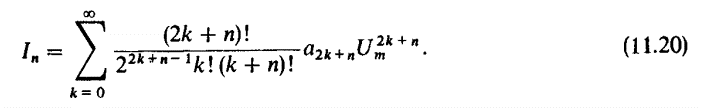Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отличия спектров при ЧМ и фм модуляции.Содержание книги
Поиск на нашем сайте
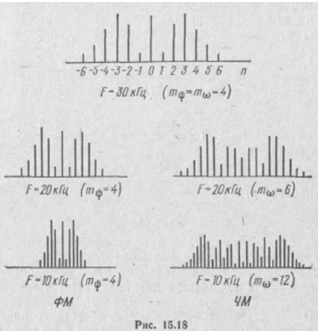
Передача широкополосных ЧМ и ФМ сигналов практически возможна только в диапазоне ультракоротких волн (УКВ). Сравнение спектра ФМ и ЧМ колебаний (рис. 15.18) показывает, что при одинаковых ωн, Ω и т их спектры ничем не отличаются.
Изменения ωн и т вызывают одинаковые изменения в спектрах ФМ и ЧМ колебаний. Отличительной особенностью спектра ЧМ колебания в сравнении с ФМ является практически независимость его ширины от частоты модуляции. При ЧМ с уменьшением Ω индекс модуляции
В случае же ФМ индекс модуляции тψ= Δψ не зависит от Ω. Поэтому с изменением Ω число учитываемых гармоник остается неизменным, а ширина спектра меняется: Для ЧМ-сигналов средняя за период высокой частоты мощность постоянна, так как амплитуда колебаний неизменна (U ω1= const). Ширина спектра ЧМ-сигнала, равна 2ωg, зависит только от амплитуды модулирующего сигнала и не зависит от его частоты. Для ФМ-колебаний средняя за период высокой частоты мощность также неизменна, ибо U ω1= const. Ширина спектра равна 2m W= 2ωg, и зависит как от амплитуды модулирующего сигнала, так и от его частоты. Таким образом, практическая ширина спектра колебаний с угловой модуляцией в m раз больше ширины спектра АМ-колебаний
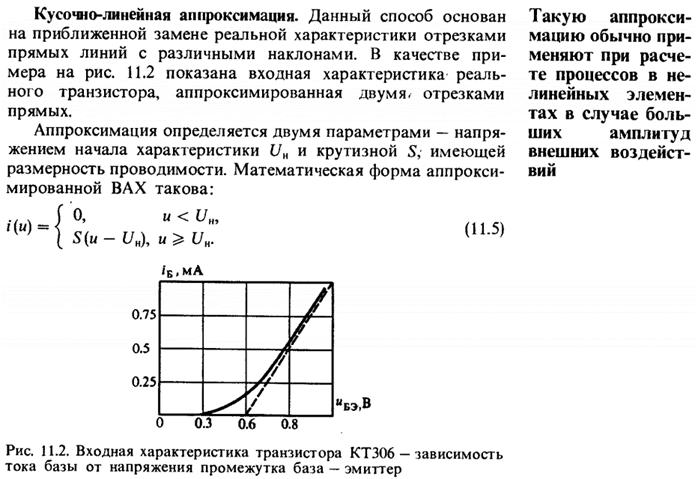
Нелинейные цепи, классификация. Методы аппроксимации характеристик нелинейных элементов и условия их применимости. (Баскаков, с. 274)
(https://ppt-online.org/117765) Классификация: · Резистивные нелинейные цепи – цепи, содержащие хотя бы один резистивный нелинейный элемент и не содержащие реактивных элементов. Процессы описываются нелинейными алгебраическими уравнениями.
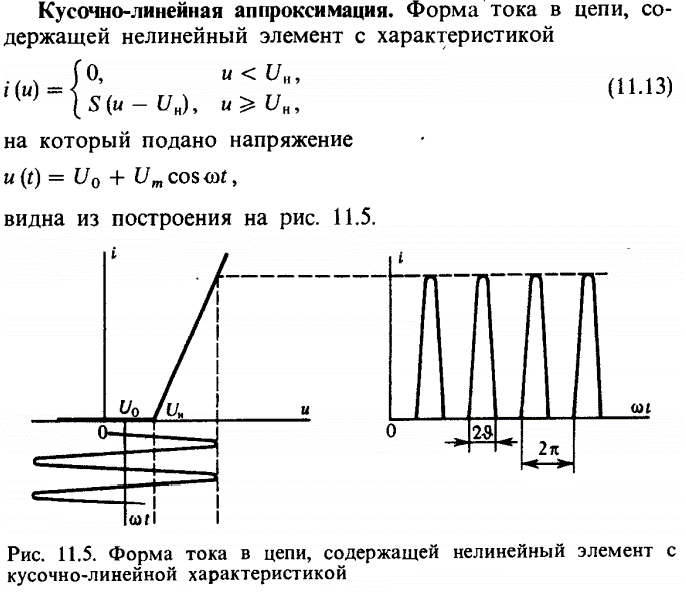
· Динамические нелинейные цепи – цепи, содержащие хотя бы один реактивный нелинейный элемент или хотя бы один реактивный элемент. Процессы описываются нелинейными дифференциальными уравнениями. (Баскаков, с. 277)
(Баскаков, с. 280)
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 1501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.008 с.) |

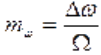 увеличивается,
увеличивается, остается неизменной. Действительно, с уменьшением Ω расстояние между спектральными линиями также уменьшится, но при ЧМ это сопровождается ростом т, что в свою очередь приводит к увеличению числа учитываемых гармоник. В результате ширина спектра практически не изменяется.
остается неизменной. Действительно, с уменьшением Ω расстояние между спектральными линиями также уменьшится, но при ЧМ это сопровождается ростом т, что в свою очередь приводит к увеличению числа учитываемых гармоник. В результате ширина спектра практически не изменяется.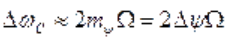 . Таким образом, ЧМ в отличие от ФМ характеризуется большим постоянством спектров сигналов, что является одной из причин предпочтительного применения ЧМ на практике. ФМ и ЧМ колебания по сравнению с АМ занимают более широкую полосу частот, но обладают двумя важными преимуществами: высокой помехоустойчивостью и возможностью обеспечить передачу более мощного сигнала при равной мощности радиопередатчика,
. Таким образом, ЧМ в отличие от ФМ характеризуется большим постоянством спектров сигналов, что является одной из причин предпочтительного применения ЧМ на практике. ФМ и ЧМ колебания по сравнению с АМ занимают более широкую полосу частот, но обладают двумя важными преимуществами: высокой помехоустойчивостью и возможностью обеспечить передачу более мощного сигнала при равной мощности радиопередатчика,