
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запишите условие ортогональности двух сигналов.Содержание книги
Поиск на нашем сайте Ортогона́льность (от греч. ὀρθογώνιος — «прямоугольный», из греч. ὀρθός — «прямой; правильный» + греч. γωνία — «угол») — понятие, являющееся обобщением перпендикулярности для линейных пространств с введённым скалярным произведением. Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу. Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот. База ШПС равна В. Чему равно ОСШ на выходе СФ, если на входе СФ ОСШ равно 1? B=dF*T
Что такое полоса когерентности канала связи и время когерентности? Для чего применяют разнесенный прием, методы комбинирования сигналов при таком приеме? Для повышения верности приема при замираниях переданное сообщение передается не по одному, а по двум или нескольким каналам связи. С этой целью могут использоваться различные средние частоты (разнесение по частоте) или передача в разные отрезки времени (разнесение по времени). Но наиболее широкое применение получил в радиосвязи метод приема сигналов на разнесенные антенны, находящиеся друг от друга на расстоянии нескольких длин волн (пространственно разнесенный прием), или принимающие различные поляризационные составляющие электромагнитного поля (поляризационно разнесенный прием). Повышение эффективности при разнесенном приеме достигается в том случае, если замирания в различных ветвях разнесения не коррелированны или слабо коррелированны друг с другом. Поэтому в то время, когда в одних ветвях уровень сигнала оказывается очень низким, в других ветвях он может быть высоким и по ним легко восстановить переданное сообщение. Если замирания в ветвях слабо коррелированны, то вероятность одновременного падения уровней в нескольких ветвях может быть достаточно мала. Пространственно–разнесенный прием, когда производится одновременный прием сигналов одного передатчика несколькими приемниками на разнесенные в пространстве антенны. Такой способ является наиболее распространенным. Параметр разнесения обычно задают в виде нормированного расстояния Частотно-разнесенный прием, когда сигналы, передаются одновременно на нескольких частотах одним или несколькими передатчиками. При частотно-разнесенном приеме величина разноса рабочих частот определяется интервалом корреляции замираний по спектру и в декаметровом диапазоне волн обычно составляет 0,5 Основной недостаток частотного разнесения состоит в расширении полосы частот, занимаемой системой связи, что приводит к увеличению взаимных помех, т.е. к ухудшению условий электромагнитной совместимости средств радиосвязи. Временной разнесенный прием осуществляется с помощью многократно передаваемых на одной и той же частоте сигналов через некоторые интервалы времени. Временное разнесение сигналов накладывает ограничения на скорость передачи информации, так как интервал повторения сигнала должен превосходить среднюю длительность замираний в канале связи. Несмотря на это, принципы временного разнесения широко используются в системах с обратной связью по решению, т.е. с автоматическим запросом ошибок и повторением информации. Эффективность того или иного метода разнесенного приема во многом определяется способом обработки разнесенных сигналов на приемной стороне. Наибольшее распространение на практике получили способы линейного сложения и автоматического выбора ветви разнесения
|
||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |

 http://mai-trt.ru/docs/edu/rtc_lab_k_04.pdf
http://mai-trt.ru/docs/edu/rtc_lab_k_04.pdf , где
, где  – проекция расстояния между антеннами на направление прихода радиоволн;
– проекция расстояния между антеннами на направление прихода радиоволн; 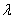 – длина волны. Очевидно, величина
– длина волны. Очевидно, величина  существенно зависит от расположения антенн относительно направления трассы связи.
существенно зависит от расположения антенн относительно направления трассы связи. 2 кГц. Частотно-разнесенный прием применяется не только для борьбы с замираниями сигналов, но и является эффективным методом повышения устойчивости KB связи при воздействии сосредоточенных по спектру помех.
2 кГц. Частотно-разнесенный прием применяется не только для борьбы с замираниями сигналов, но и является эффективным методом повышения устойчивости KB связи при воздействии сосредоточенных по спектру помех.


