
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концентрация в сетях передачи данных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Концентрация в сетях передачи данных Для того чтобы обеспечить выполнение всех требований, которые предъявляются абонентами, сеть ПД должна обладать определенной пропускной способностью, т. е. возможностью передачи в единицу времени требуемого объема информации. Передаваемый по сети объем информации определяется производительностью включенных в нее источников информации и характером их работы. На рис.5.3 показано изменение интенсивности нагрузки на входе в систему распределения информации УК сети ПД. Эту систему можно построить так, что ее пропускная способность будет соответствовать прямой АВ, т. е. она сможет про- пустить весь поток информации даже в моменты пиковых значений без отказов и задержек. Однако такая система была бы неэкономична, так как в остальные промежутки времени, продолжительность которых значительно превосходит периоды пиков нагрузки, ее пропускная способность используется неполностью.
Интуитивно более удачной представляется система, пропускная способность которой соответствует прямой ВГ на рис.5.7. В пиковые моменты обрабатывается только часть поступающей нагрузки; остальная нагрузка обрабатывается несколько позднее—в пределах заштрихованных областей, расположенных ниже прямой ВГ. Заштрихованные области, лежащие выше прямой ВГ, не должны превышать области, расположенные ниже ее. В противном случае, когда пропускная способность представляется прямой ДЕ, система окажется не в состоянии обработать весь поток информации, т. е. возникает перегрузка системы. На принципе сглаживания пиковых нагрузок неравномерного потока информации основан процесс концентрации, широко используемый в сетях ПД для повышения использования пропускной способности каналов и устройств распределения информации в УК. В отличие от статической процедуры разделения каналов в многоканальных системах передачи, концентрация представляет собой динамическую процедуру распределения меньшего числа выходных каналов в соответствии со случайным характером потока сообщений, поступающего от большого числа входных каналов. Концентрация по существу происходит только во времени, так как она учитывает неравномерность потока сообщений во времени. Техническая реализация устройств концентрации может быть пространственной или временной. В обоих случаях система может иметь или не иметь устройства памяти. При наличии бесконечно большой памяти это будет система с ожиданием, при конечной памяти с ожиданием и отказами при отсутствии памяти—с отказами. Пространственная концентрация осуществляется с помощью устройств, которые электрически подключают группу из л входов (каналов) к группе из т выходов (каналов), причем п>т. При этом входные и выходные каналы обычно имеют одинаковые характеристики (полосу частот, скорость передачи). Устройства пространственной концентрации широко применяются в сочетании с системами передачи с пространственным, частотным и синхронным временным разделением сигналов. Временная концентрация осуществляется на принципах асинхронно-временного разделения сигналов. При пространственной концентрации обычно осуществляется концентрация целых сообщений или групп сообщений, т. е. выходной канал j предоставляется входному каналу i на все время передачи одного или нескольких сообщений. При асинхронной временной концентрации выходной канал j может предоставляться входному каналу i для передачи как целых сообщений, так и отдельных частей: слов, знаков единичных элементов, ЗМ. Вследствие этого, асинхронно-временная концентрация может обеспечить большую эффективность (отношение числа входных к выходным каналам), чем пространственная, так как использует не только паузы между входящими сообщениями, но и паузы внутри сообщений. Поэтому в ряде случаев асинхронно-временную концентрацию применяют в качестве дополнительной ступени концентрации в системах с пространственной коммутацией и разделением (так называемое «статистическое уплотнение»). Процесс концентрации лежит в основе построения коммутируемых сетей связи. При переходе от некоммутируемой сети к сети с децентрализованной системой коммутации на основе эффекта концентрации уменьшается число входов-выходов ОП и соответственно сокращено число соединительных линий ОП с УК. Так же с помощью концентрации может быть сокращено оборудование распределения информации по адресу (уменьшено число точек коммутации) в сети с централизованной коммутацией. Отмеченный технико-экономический эффект за счет концентрации создается не безвозмездно, а ценой ухудшения качественных показателей системы: возникновением отказов или задержек в передаче информации, которые отсутствуют в системах без концентрации (например, некоммутируемых сетях). Вопросы к государственному экзамену дисциплина «Моделирование систем связи» Лутченко С.С. Заочное обучение Г МСС 11 сем.
Многолучево́е распростране́ние — это эффект, наблюдаемый при распространении сигналов. Возникает при условии существования в точке приема радиосигнала не только прямого, но и ещё одного или целого ряда отражённых лучей. Другими словами, на антенну приёмника приходят не только прямые лучи (непосредственно от самого источника), но и отражённые (от земной поверхности, зданий, строений и прочих объектов). Однолучевое распространение – космос – провод
ЛЕКЦИЯ 4. Модель однолучевого дискретного канала связи Вероятность ошибок в дискретных каналах связи зависит от отношения сигнал/помеха и описывается выражением (1.3). Отношение сигнал/помеха Н зависит от уровня сигнала, скорости манипуляции и спектральной плотности мощности помех на входе демодулятора (1.4). Спектральная плотность мощности помех n2 содержит два основных компонента: спектральную плотность атмосферного шума n2аш и спектральную плотность станционных помех n2сп. Амплитуда сигнала A и спектральная плотность мощности станционных помех n2сп, как правило, все время меняют свое значение из-за условий распространения декаметровых радиоволн в атмосфере. Поэтому вероятность ошибки в дискретных каналах связи декаметрового диапазона радиоволн является функцией времени. Для моделирования потока ошибок в этих каналах связи необходимо произвести моделирование амплитуды сигнала и спектральной плотности мощности станционных помех как случайных функций времени. Далее будем считать, что амплитуда сигнала может меняться по законам изменения модуля вектора нормального двумерного марковского случайного процесса в соответствии с задаваемыми параметрами этого процесса, а уровень станционных помех изменяется по закону Релея. Частными случаями замираний сигнала являются релеевские (регулярная составляющая равна нулю, коэффициент взаимной корреляции квадратур случайного компонента равен нулю), райсовские (коэффициент взаимной корреляции квадратур равен нулю, регулярная составляющая не равна нулю) и односторонние усеченные нормальные (коэффициент взаимной корреляции квадратур равен единице). Если в последнем случае регулярная составляющая равна нулю, то имеет место односторонний нормальный закон замираний сигнала, который является самым неблагоприятным. Задавая значения коэффициента взаимной корреляции квадратур в пределах интервала [0, 1], можно получать законы замираний, имеющие промежуточный вид между вышеперечисленными. Алгоритмы формирования двумерных марковских процессов с модулями векторов, имеющих требуемые распределения вероятностей, описаны в гл. 3. Каждый отдельно взятый сеанс связи может проходить с присутствием или отсутствием станционной помехи. Появление помехи является случайным событием и определяется соответствующей вероятностью. Кроме того, уровни помех в отдельных сеансах могут существенно отличаться друг от друга. Известно, что средние уровни помех в различных сеансах связи хорошо описываются логарифмически нормальным законом распределения [22]:
Uсп = 100,05[СКОспРспCOS(2пR1) + МОсп], (4.1)
где МОсп и СКОсп - матожидание и среднеквадратическое отклонение логнормального закона в децибелах;
Рсп =
В формулах (4.1) и (4.2) R1 и R2 - случайные числа на интервале [ 0, 1 ]. На рис. 4.1 изображена блок-схема обобщенного алгоритма модели однолучевого дискретного канала связи с замираниями и станционными помехами. В соответствии с этим алгоритмом была разработана программа“FEDING-1”. Эта программа дает возможность имитировать одиночные сеансы связи с различными видами манипуляции (амплитудной, частотной и относительной фазовой), различной скоростью манипуляции, различными видами замираний сигнала, в присутствии или отсутствии станционных помех. Необходимо учитывать тот факт, что программа “FEDING-1” не отражает доплеровских эффектов, которые могут иметь место в реальном КВ канале связи, и поэтому результаты, получаемые для режима ОФТ, могут считаться корректными только при относительно высоких скоростях манипуляции (выше 250 бод). Входными данными программы являются: - вид манипуляции (для декодера); - скорость манипуляции; - число знаков в телеграмме; - время корреляции замираний сигнала и станционных помех; - среднее значение амплитуды флуктуирующего компонента сигнала; - коэффициент взаимной корреляции квадратур случайной составляющей сигнала, который определяет характер закона замираний; - амплитуда регулярной составляющей сигнала; - спектральная плотность мощности шума; - вероятность появления станционных помех; - МО распределения уровней станционных помех в децибелах; - СКО распределения уровней станционных помех в децибелах; - номер сеанса связи; - начальное квазислучайное число; - коэффициент энергетических потерь (из-за возможных отклонений от оптимальных схемотехнических решений). Выходными данными программы являются: - график зависимости от времени отношения сигнал/помеха (дисплей); - график зависимости уровня спектральной плотности мощности станционных помех (дисплей); - векторы ошибок элементов для АТ, ЧТ и ОФТ демодуляторов (дисплей); - данные о количестве ошибок в отдельных кодовых комбинациях (файл, дисплей и принтер);
ВВОД входных данных
Формирование для всех независимых процессов начальных случайных чисел с помощью вспомогательного ГСЧ на основе введенного общего начального числа
Формирование значения амплитуды сигнала
Формирование значения амплитуды помехи
Вычисление отношения сигнал / помеха
Определение вероятности ошибки элемента сообщения
Определение факта появления ошибки элемента сообщения
Формирование вектора ошибок элементов сообщения
- отношения сигнал / помеха; -уровня станционных помех; -векторов ошибок элементов
НЕТ
?
Формирование векторов стирания и ошибок знаков сообщения
ВЫВОД протокола испытаний ВЫВОД гистограммы отношения сигнал / помеха
Вычисление теоретических значений распределения вероятности отношения сигнал / помеха
ВЫВОД графика распределения вероятности отношения сигнал / помеха
КОНЕЦ
Рис. 4.1
- для заданного вида демодулятора выводится вектор ошибок знаков при использовании семиэлементного кода с проверкой на четность (файл, дисплей и принтер); - гистограмма распределения значений отношения сигнал/помеха (дисплей); - графики плотности вероятности релеевского, райсовского (обобщенного релеевского), одностороннего усеченного нормального распределения и распределения Накагами (дисплей). После окончания сеанса связи программа для указанного номера сеанса создает файл с протоколом испытаний. Кроме того, программа предусматривает режим работы с распечатыванием протокола испытаний и выводом его на дисплей. В программе предусмотрено также запоминание введенных исходных данных, что позволяет повторять сеансы с необходимой оперативной корректировкой отдельно взятых параметров. В программе имеется демонстрационный режим работы, который позволяет подготовить заранее необходимые входные данные для оперативной демонстрации работы модели. В данном варианте модели использован 7-элементный код с проверкой на четность. Для другого вида кода необходимо изменить подпрограмму, которая соответствует декодеру. В табл. 4.1-4.3 приведены примеры протоколов, выводимых на печать после проведения сеансов связи. Таблица 4.1
П Р О Т О К О Л N 1 Файл: D:\HF-KANAL\PERFORAT\sns 1 08-20-1997 АТ Количество элементов в сообщении: 70 Количество ошибочно принятых элементов: 7 Оценка вероятности ошибочного приема элемента:.10E+00 ========================================================= N ВЕКТОР ОШИБОК КОЛ-ВО ОШИБОК РЕЗУЛЬТАТ ========================================================= 1 0 0 1 0 0 0 0 1 СТЕРТО 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 1 0 1 СТЕРТО 6 0 0 0 0 0 1 0 1 СТЕРТО 7 0 0 1 0 1 0 0 2 1 8 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 1 0 1 СТЕРТО 10 0 0 0 0 0 1 0 1 СТЕРТО ========================================================= Количество правильно принятых знаков: 4 Количество ошибочно принятых знаков: 1 Количество стертых знаков: 5 Оценка вероятности непринятого знака:.60E+00
Таблица 4.2
П Р О Т О К О Л N 2 Файл: D:\HF-KANAL\PERFORAT\sns 2 08-20-1997 ЧТ Количество элементов в сообщении: 70 Количество ошибочно принятых элементов: 3 Оценка вероятности ошибочного приема элемента:.43E-01 ========================================================= N ВЕКТОР ОШИБОК КОЛ-ВО ОШИБОК РЕЗУЛЬТАТ ========================================================= 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 1 0 1 СТЕРТО 7 0 0 0 0 1 0 0 1 СТЕРТО 8 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 1 0 1 СТЕРТО ========================================================= Количество правильно принятых знаков: 7 Количество ошибочно принятых знаков: 0 Количество стертых знаков: 3 Оценка вероятности непринятого знака:.30E+00
Таблица 4.3
П Р О Т О К О Л N 3 Файл: D:\HF-KANAL\PERFORAT\sns 3 08-20-1997 ОФТ Количество элементов в сообщении: 70 Количество ошибочно принятых элементов: 0 Оценка вероятности ошибочного приема элемента:.00E+00 ========================================================= N ВЕКТОР ОШИБОК КОЛ-ВО ОШИБОК РЕЗУЛЬТАТ ========================================================= 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 ========================================================= Количество правильно принятых знаков: 10 Количество ошибочно принятых знаков: 0 Количество стертых знаков: 0 Оценка вероятности непринятого знака:.00E+00
Данные сеансы были проведены в абсолютно одинаковых условиях и отличались только видами манипуляции параметров несущего колебания. В заключение рассмотрим отдельные алгоритмы, которые соответствуют фрагментам программы, посвященным теоретическим расчетам значений распределений отношения сигнал/помеха (без учета станционных помех) для случая релеевских, райсовских, усеченных односторонних нормальных замираний и замираний, происходящих по закону m-распределения. Распределение Релея: P(h) = h / exp(((h / so)2) / 2) / (so)2; (4.3)
so = СKO × (10 0,05Ко) / (n
СKO = Acp ×
где Acp - среднее значение амплитуды сигнала; n2 - спектральная плотность мощности шума; Ko - коэффициент энергетических потерь, обусловленный неоптимальностью тракта аппаратуры; V - скорость манипуляции.
Распределение Райса (обобщенное релеевское распределение): Р(h) = h × Io / ехр(((h2 + h
hp = Ap × (10 0,05Ko) / (n
где Ap - амплитуда регулярной составляющей сигнала; Io - модифицированная функция Бесселя 1- го рода нулевого порядка. Блок-схема алгоритма определения значений модифицированной функции Бесселя 1-го рода нулевого порядка приведена на рис. 4.2. В основу алгоритма положена соответствующая программа, опубликованная в [29].
Усеченное одностороннее распределение Гаусса (усеченное одностороннее нормальное распределение): Р (h) = 1 / ехр{[((h - hp) / so)2 ] / 4} / so / + 1 / ехр{[((h + hp) / so)2] / 4} / so /
ВВОД: h; hp; Sigma0
x = h * hp / Sigma0 ^ 2
S = 1; I = 1; B = 1
y = (x / 2) ^ 2
I = I + 1; B = B * I
z = y ^ I / B ^ 2
S = S + z
ДА
НЕТ
Io = S
ВЫВОД: Io
КОНЕЦ
Рис. 4.2
Распределение Накагами (m-распределение): Р (h) = 2 mm (h / (
где Г(m) - гамма-функция, которая описывается выражением [33]:
Г(m) =
Блок-схема алгоритма для определения значений гамма-функции c точностью до пятого знака при условии, что m < 50, приведена на рис. 4.3. Этот алгоритм соответствует программе, опубликованной в [29] и базирующейся на формуле Стирлинга для приближенного представления гамма-функции:
Нужно заметить, что при m = 1 / 2 m-распределение вырождается в одностороннее нормальное распределение, а при m = 1 - соответственно в Релеевское распределение.
НАЧАЛО

ВВОД значения параметра m
z = m; x = z; a = 1

I = 0
I = I + 1

z = z * (x + 1)
ДА?
y = x + 21

Г(m) = exp(y * (ln(y) - 1) +1 / 12 / y) * SQR(2 * п / y) / z
ВЫВОД Г(m)
КОНЕЦ
Рис. 4.3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |


 . (4.2)
. (4.2) НАЧАЛО
НАЧАЛО













 ВЫВОД на экран дисплея графиков:
ВЫВОД на экран дисплея графиков:

 Конец сеанса
Конец сеанса ДА
ДА








 ); (4.4)
); (4.4) , (4.5)
, (4.5) ) / (so)2 ) / 2) / (so)2; (4.6)
) / (so)2 ) / 2) / (so)2; (4.6) / 2 +
/ 2 +












 z > 1E-09
z > 1E-09 ?
?




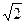 so))2m-1 ехр(-m (h / (
so))2m-1 ехр(-m (h / ( (m > 0). (4.10)
(m > 0). (4.10) . (4.11)
. (4.11)







 I < 20
I < 20 НЕТ
НЕТ





