
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы комбинирования и коммутации при разнесенном приемеСодержание книги
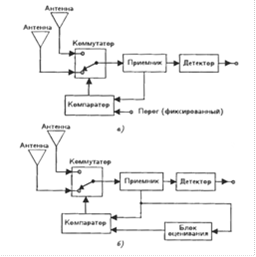
Поиск на нашем сайте Существует несколько методов комбинирования некоррелированных сигналов при разнесенном приеме. Обычно они классифицируются по следующим трем категориям: ) оптимальное (по критерию максимального отношения сигнал/помеха) сложение, ) сложение с равными весами, ) автовыбор. При когерентной демодуляции характеристики додетекторного и последетекторного сложения оказываются одинаковыми. Однако при некогерентной демодуляции цифровых ЧМ сигналов, осуществляемой с помощью дискриминатора или автокорреляционного демодулятора, характеристики додетекторного и последетекторного сложения оказываются различными. На Рис.2 приведены структурные схемы, иллюстрирующие методы додетекторного комбинирования. При идеальной реализации метод оптимального додетекторного сложения обеспечивает максимальное улучшение характеристик помехоустойчивости по сравнению с другими методами. Однако для него требуются блоки фазирования, весовой обработки и сложения (рис.2, а), что существенно усложняет его реализацию. Структурная схема, иллюстрирующая метод сложения с равными весами, изображена на рис.2, б. Она во многом схожа со схемой оптимального сложения за исключением того, что в ней отсутствуют блоки весовой обработки. Улучшение характеристик помехоустойчивости, обеспечиваемое сложением с равными весами, по сравнению с оптимальным сложением, оказывается несколько меньше, поскольку помехи и шум, искажающие сигнал и содержащиеся в "зашумленных" ветвях разнесения, могут суммироваться с "чистыми" сигналами ветвей разнесения, не содержащими помех. Для ОВЧ, УВЧ и микроволновых систем подвижной радиосвязи методы оптимального сложения и сложения с равными весами представляются малопригодными. Это связано с трудностями реализации блока фазирования, обеспечивающего необходимую точность и устойчивость характеристик сложения в условиях замираний из-за многолучевости, порождающих быстрые случайные изменения фазы. По сравнению с этими двумя методами комбинирования метод автовыбора в силу простоты реализации представляется более приспособленным для применения в системах подвижной радиосвязи. Согласно этому методу всякий раз выбирается наилучшая ветвь разнесения, т.е. ветвь с максимальным уровнем сигнала (в более современных системах выбирается ветвь с минимальным значением Рс) (см. рис.2, в). Кроме того, устойчивая работа здесь может быть обеспечена даже в условиях быстрых замираний из-за многолучевости. По сравнению с предельным улучшением характеристик помехоустойчивости, обеспечиваемым оптимальным сложением, их улучшение при автовыборе оказывается несколько меньше.
Рис. 2. Структуры методов комбинирования сигналов при разнесенном приеме: а - оптимальное сложение; б - сложение с равными весами; в - автовыбор. Главный недостаток этого метода состоит в том, что при его реализации требуется иметь ровно столько приемных каналов с непрерывным контролем, сколько необходимо иметь ветвей разнесения. Этого недостатка лишены приемники с переключением или сканированием. На рис.3 приведены структурные схемы подобных приемников.
Рис.3 Методы автовыбора с фиксированным (а) и переменным (б) порогами. Хотя метод автовыбора с фиксированным порогом проще при реализации и характеризуется большим быстродействием, но невозможно выбрать значение порога, оптимальное для всей области обслуживания. Введение обратной связи решает эту проблему, но может вызвать искажения огибающей и фазы. В схеме, изображенной на рис.3, а, переключение ветвей разнесения происходит всякий раз, когда уровень сигнала ниже порога. Порог может устанавливаться фиксированным только для небольшой области обслуживания, и он не является наилучшим для всей области. Поэтому уровень порога должен адаптивно подстраиваться при перемещении подвижного объекта, как показано на рис.3, б. Улучшение характеристик помехоустойчивости, достигаемое при использовании метода переключения, зависит от точности установки порога, временной задержки в цепи обратной связи, необходимой для выполнения контроля, оценивания, принятия решения и осуществления переключения. Следует также отметить, что переходные процессы, возникающие в ВЧ каскадах при переключении и вызывающие искажение огибающей и фазы сигнала несущей, могут снизить достигаемое улучшение. При угловой модуляции, используемой в системе GSM, искажения фазы из-за переходных процессов будут вызывать появление ошибок в демодулированных данных, а искажения огибающей могут быть устранены с помощью предмодуляционных полосовых ограничителей. В Приложении приведены схемы формирования сигналов для стандарта GSM, устойчивых к возможным искажениям. Там же рассмотрены их разновидности, запатентованные Феером.
Рис.4
Двоичный линейный блочный код предусматривает формирование из Si + Sj S информационных битов блока из n кодированных битов. Кодированные и информационные биты принимают значение 0 или 1. поэтому такой код называют (n.K)-двоичным кодом. Группа из n кодированных битов может принимать 2^n возможных значений, соответствующих всем возможным комбинациям из n двоичных битов. Из этих 2^n возможных состояний выбираются 2^k кодовых слов так, чтобы каждый Si + Sj S битовый информационный блок однозначно преобразуется в одно из этих 2^k кодовых слов. Скорость кода составляет Rc = k/n бит/с. Если предположить, что кодированные символы передаются по каналу со скоростью передачи символов Rs символов/с, то информационная скорость с учетом использования (n.k)-блочного кода составляет Rb = RcRs = kRs/n бит/с Таким образом, видно, что блочное кодирование уменьшает скорость передачи данных по сравнению с той, которую мы получаем при некодированной модуляции со скоростью Rc. Блочный код называют линейным, когда преобразование k информационных битов в n кодированных битов представляет собой линейное преобразование. Для описания этого преобразования и соответствующих функций кодирования и декодирования более подробно необходимо первоначально рассмотреть свойства векторного пространства двоичных кортежей из n элементов и соответствующих им подпространств. Множество всех двоичных кортежей из n элементов Вn является векторным пространством в пределах двоичного поля, которое состоит из двух элементов 0 и 1. Все поля предусматривают две операции — сложение и умножение: для двоичного поля эти операции соответствуют двоичному сложению (сложению по модулю 2) и стандартному умножению. Подмножество S величины Вn называют подпространством, если оно удовлетворяет следующим условиям: 1) вектор, все элементы которого нули, находятся в S; 2) множество S является замкнутым при сложении, таким образом, если Si S и Sj S, то и Si + Sj S Блочный (n, k)-код является линейным, если 2^k кодовых слова длиной n образуют подпространство Вn. Таким образом, если Сi и Gj — два кодовых слова в (n, k)-линейном блочном коде, то тогда Сi = Со должно составить другое кодовое слово кода. Интуитивно понятно, что чем больше расстояние между кодовыми словами в данном коде, тем меньше вероятность того, что ошибки, вводимые каналом, будут трансформировать передаваемое кодовое слово при декодировании в другое кодовое слово. Хэммингово расстояние между двумя кодовыми словами (или последовательностями) Сi и Со обозначается как d(Сi,Со), или dij и определяется числом элементов, на которое они различаются: Порождающая матрица — это компактное описание того, каким образом информационные биты преобразуются в линейный блочный код. Основная цель разработки линейных блочных кодов заключается в нахождении порождающих матриц, которые позволяют получить коды, легко обрабатываемые при кодировании и декодировании и при этом обладающие хорошими возможностями для обнаружения и исправления ошибок. Источник: http://systemseti.com/CCPO/428.html MedUniver Циклический код — линейный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок (см. Обнаружение и исправление ошибок). Содержание
Введение Пусть Это позволяет рассматривать множество слов длины n над конечным полем как линейное пространство полиномов со степенью не выше n-1 над полем Алгебраическое описание Если
Сдвиг вправо и влево соответственно на
Если Порождающий полином Определение Порождающим полиномом циклического Теорема 1 Если
где степень Теорема 2
Следствия: таким образом в качестве порождающего полинома можно выбирать любой полином, делитель Порождающая матрица Полиномы Значит кодовые слова можно записывать, как и для линейных кодов, следующим образом:
Матрицу Проверочная матрица Для каждого кодового слова циклического кода справедливо
Тогда:
Кодирование Несистематическое При несистематическом кодировании кодовое слово получается в виде произведения информационного полинома на порождающий
Оно может быть реализовано при помощи перемножения полиномов. Систематическое При систематическом кодировании кодовое слово формируется в виде информационного подблока и проверочного Пусть информационное слово образует старшие степени кодового слова, тогда
Тогда из условия
Это уравнение и задает правило систематического кодирования. Оно может быть реализовано при помощи многотактных линейных фильтров(МЛФ) Примеры Двоичный (7,4,3) код В качестве делителя Порождающая матрица кода:
где первая строка представляет собой запись полинома Проверочная матрица:
где i-ый столбец, начиная с 1-го, представляет собой остаток от деления Так, например, 4-й столбец получается Легко убедиться, что Двоичный (15,7,5) БЧХ код В качестве порождающего полинома
Тогда каждое кодовое слово можно получить с помощью произведения информационного полинома
Например, информационному слову Блоковые коды Пусть кодируемая информация делится на фрагменты длиной Если исходные Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач. Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
|
||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 777; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |



 слово длины n над алфавитом из элементов конечного поля
слово длины n над алфавитом из элементов конечного поля  и
и 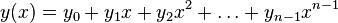 полином, соответствующий этому слову, от формальной переменной
полином, соответствующий этому слову, от формальной переменной  . Видно, что это соответствие является изоморфизмом линейных пространств. Так как «слова» состоят из букв из поля, то их можно складывать и умножать (поэлементно), причём результат будет в том же поле. Полином, соответствующий линейной комбинации
. Видно, что это соответствие является изоморфизмом линейных пространств. Так как «слова» состоят из букв из поля, то их можно складывать и умножать (поэлементно), причём результат будет в том же поле. Полином, соответствующий линейной комбинации  пары слов
пары слов  и
и  , равен линейной комбинации полиномов этих слов
, равен линейной комбинации полиномов этих слов 

 кодовое слово, получающееся циклическим сдвигом на один разряд влево из слова
кодовое слово, получающееся циклическим сдвигом на один разряд влево из слова  , то соответствующий ему полином
, то соответствующий ему полином 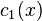 получается из предыдущего умножением на x:
получается из предыдущего умножением на x: , пользуясь тем, что
, пользуясь тем, что  ,
, разрядов:
разрядов: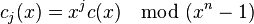
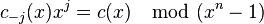
 — произвольный полином над полем
— произвольный полином над полем  и
и  — кодовое слово циклического
— кодовое слово циклического  кода, то
кода, то 
 тоже кодовое слово этого кода.
тоже кодовое слово этого кода. называется такой ненулевой полином
называется такой ненулевой полином  из
из  .
.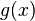 — его порождающий полином, тогда степень
— его порождающий полином, тогда степень  и каждое кодовое слово может быть единственным образом представлено в виде
и каждое кодовое слово может быть единственным образом представлено в виде ,
, .
.
 , число информационных символов
, число информационных символов  .
. линейно независимы, иначе
линейно независимы, иначе  при ненулевом
при ненулевом  , где
, где  является порождающей матрицей,
является порождающей матрицей, 
 . Поэтому проверочную матрицу можно записать как:
. Поэтому проверочную матрицу можно записать как:



 , следует
, следует
 выберем порождающий полином третьей степени
выберем порождающий полином третьей степени  , тогда полученный код будет иметь длину
, тогда полученный код будет иметь длину  , число проверочных символов (степень порождающего полинома)
, число проверочных символов (степень порождающего полинома)  , число информационных символов
, число информационных символов  , минимальное расстояние
, минимальное расстояние  .
. ,
, ,
, на полином
на полином  , или в векторной записи
, или в векторной записи  .
.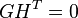 .
. :
: .
.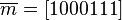 соответствует полином
соответствует полином  , тогда кодовое слово
, тогда кодовое слово  , или в векторном виде
, или в векторном виде 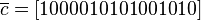
 бит, которые преобразуются в кодовые слова длиной
бит, которые преобразуются в кодовые слова длиной  бит. Тогда соответствующий блоковый код обычно обозначают
бит. Тогда соответствующий блоковый код обычно обозначают  называется скоростью кода.
называется скоростью кода. проверочных, такой код называется систематическим, иначе несистематическим.
проверочных, такой код называется систематическим, иначе несистематическим.


