
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквивалентная схема линейного трансформатора. Анализ схемы при гармоническом воздействии коэффициенты трансформации.Содержание книги
Поиск на нашем сайте
Реальные линейные трансформаторы применяются: для гальванической развязки электрических цепей; для передачи энергии с преобразованием величин тока или напряжения; для передачи сигналов в усилителях или автогенераторах; для согласования сопротивлений.
В соответствии со вторым законом Кирхгофа система уравнений для контуров имеет вид:
На одной клемме вторичной обмотки трансформатора напряжений будет в фазе, а на другой – в противофазе в сравнении с входным напряжением. Это следует из того, что ток первичной обмотки отстает от входного напряжения на Для встречного включения коэффициенты передачи по току и напряжению трансформатора при решении системы уравнений (5.11), (5.12) запишутся в виде Из выражений (5.13), (5.14) следует, что коэффициенты передачи трансформаторов зависят от большого числа параметров, что следует учитывать при проектировании реальных трансформаторов. Согласующие трансформаторы проектируют с большим значением индуктивности первичной обмотки и минимальными потерями. С учетом этого выражения (5.13), (5.14) при условии
Такой идеализированный трансформатор называется «идеальным» и передает всю мощность из первичной обмотки в вторичную, т.е. P1 = P2 или
Последнее выражение используется для расчета коэффициента трансформации, требуемого по условиям согласования по мощности. Так как индуктивности реальных катушек пропорциональны квадрату числа витков, т.е.
Выражения (5.15), (5.16), (5.19) часто применяются в расчетах с любыми трансформаторами, однако ошибки расчета будут тем больше, чем больше отличается реальный трансформатор от идеального. 1.7. Переходные процессы в линейных электрических цепях. Основные определения. Основные методы анализа. Переходные процессы в линейных электрических цепях. Основные определения. Основные методы анализа. В реальных электрических цепях происходят переключения радиоэлементов, включения и выключения источников электрической энергии, источников переменных сигналов. При переключениях (коммутациях) происходит переход цепи от одного установившегося состояния к другому, то есть изменение энергетических состояний. Для практических целей (правильной эксплуатации, оценки надежности) необходимо знать: − вид переходных процессов на разных участках цепи; − время завершения переходного процесса (время установления); − максимальные значения токов и напряжений при переходных процессах. Длительность переходных процессов определяет готовность радиоаппаратуры к работе, а «броски» токов и напряжений при переключениях могут вывести радиоэлементы из строя. Переходный процесс объясняется изменением энергетических состояний реактивных элементов цепи, поэтому в идеальной цепи, состоящей только из резистивных элементов, переходные процессы отсутствуют. Основные определения: − − независимые начальные условия − начальные условия для момента времени − зависимые начальные условия − начальные условия для момента времени − электрическая цепь с нулевыми начальными условиями − в момент времени − электрическая цепь с ненулевыми начальными условиями − в момент времени − корректные переключения (коммутации) − законы коммутации не противоречат основным законам цепей и их можно применять для анализа; − некорректные коммутации − законы коммутации противоречат теории цепей и для анализа необходимо вначале применить более общие принципы непрерывности потокосцепления и заряда. Математический аппарат: −классический способ решения линейных дифференциальных уравнений; −интегральные преобразования Фурье; −интегральные преобразования Лапласа; −интегралы наложения.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |



 , а затем еще дает дополнительный фазовый сдвиг
, а затем еще дает дополнительный фазовый сдвиг  сопротивление связи (
сопротивление связи ( ).
). ,(5.13)
,(5.13)  . (5.14)
. (5.14) -> Ґ;
-> Ґ; 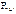 = 0;
= 0;  = 0;
= 0;  , преобразуются к виду
, преобразуются к виду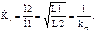 (5.15)
(5.15) (5.16)
(5.16) (5.17) где
(5.17) где 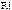 − сопротивление источника сигнала в первичном контуре, а
− сопротивление источника сигнала в первичном контуре, а  − сопротивление нагрузки во вторичном контуре.
− сопротивление нагрузки во вторичном контуре. (5.18)
(5.18) , то коэффициент трансформации идеального трансформатора равен
, то коэффициент трансформации идеального трансформатора равен . (5.19)
. (5.19) ,
, 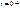 − время, соответственно, непосредственно до и после переключения;
− время, соответственно, непосредственно до и после переключения; ;
; ;
; реактивные элементы не имели энергии;
реактивные элементы не имели энергии;


