
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонический сигнал, основные характеристики. Временная и спектральные диаграммы сигнала. Воздействие гармонического сигнала на линейные радиоэлементы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Гармонический сигнал, основные характеристики. Временная и спектральные диаграммы сигнала. Воздействие гармонического сигнала на линейные радиоэлементы. Гармонические сигналы формируются генератором гармонических колебаний и применяются в качестве управляющих или несущих колебаний. В теории электрических цепей для записи гармонических сигналов чаще используется тригонометрическая функция косинус, например,
Для сравнения с источниками постоянного тока для переменных сигналов введено действующее значение, по тепловому действию аналогичное действию постоянного тока
Временная диаграмма:
Спектральные диаграммы: амплитудный спектр и фазовый спектр сигнала. Для гармонического сигнала:
Линейные радиоэлементы: резистивный элемент – сопротивление R, индуктивный элемент – индуктивность L, емкостной элемент – емкость С. − идеализированные элементы на гармоническом токе ведут себя по-разному. Элемент Инерционность реактивных элементов в данном случае означает следующее: для индуктивности временная диаграмма напряжения опережает временную диаграмму тока на
Учет полного сопротивления идеализированных элементов (модуля и аргумента) позволяет проводить расчеты последовательных и параллельных цепей методом векторных треугольников. В этом методе напряжениям и токам на элементах эквивалентной схемы придают смысл векторов, длины которых равны амплитудам сигналов, а углы наклонов – начальным фазовым сдвигам. С помощью законов Кирхгофа качественно (без соблюдения масштаба) строятся векторные треугольники напряжений и подобные им треугольники сопротивлений для последовательных цепей или схем и треугольники токов и проводимостей для параллельных цепей или схем. Для последовательных схем построение векторных диаграмм начинается с вектора тока, для параллельных - с вектора напряжения. По известным параметрам источников энергии, величинам элементов определяют неизвестные величины.
1.2. Комплексные преобразования гармонических сигналов. Комплексные амплитуды и сопротивления. Законы электрических цепей в комплексной форме. Комплексные преобразования гармонических сигналов. Комплексные амплитуды и сопротивления. Законы электрических цепей в комплексной форме. Более универсальным методом анализа является применение комплексного преобразования, при котором гармонические сигналы одной и той же частоты применением преобразования (3.4) заменяются комплексными числами (символами), не содержащими времени. Так как комплексное преобразование является интегральным, то для него справедливы все свойства интегралов, например: − постоянный множитель можно выносить за знак интеграла; − интеграл от суммы функций равен сумме интегралов. Отсюда следует справедливость всех законов и теорем электрических цепей в комплексном виде, а также справедливость рассмотренных в разделе 2 методов анализа. Например, запись основных законов теории цепей с использованием комплексных амплитуд сигналов имеет следующий вид
Например, для схемы с последовательным включением генератора гармонического колебания, резистора, индуктивности и емкости по 2 закону Кирхгофа: Преобразуем это выражение в комплексный вид, получаем
В выражении (3.15):
Так как принцип перевода гармонических сигналов в комплексный вид вполне очевиден, то комплексное преобразование служит скорее для пояснения справедливости законов теории цепей при использовании комплексных амплитуд, а не для постоянного применения при анализе эквивалентных схем.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.007 с.) |

 , где
, где  − амплитуда сигнала;(
− амплитуда сигнала;( ) − полная фаза сигнала, в рад;
) − полная фаза сигнала, в рад;  − начальная фаза сигнала, в рад;
− начальная фаза сигнала, в рад;  − циклическая частота, в рад/с;
− циклическая частота, в рад/с;  − текущая частота, в Гц;
− текущая частота, в Гц;  − период колебаний.
− период колебаний. . В действующих значениях калибруется большинство измерительных приборов, измеряющих токи или напряжения переменных сигналов.
. В действующих значениях калибруется большинство измерительных приборов, измеряющих токи или напряжения переменных сигналов.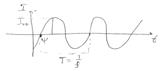


 не инерционный, не вносит дополнительного сдвига фазы. Элемент
не инерционный, не вносит дополнительного сдвига фазы. Элемент  инерционный, модуль его сопротивления
инерционный, модуль его сопротивления  , фазовый сдвиг (аргумент)
, фазовый сдвиг (аргумент)  . Элемент
. Элемент  инерционный, модуль его сопротивления
инерционный, модуль его сопротивления  , фазовый сдвиг
, фазовый сдвиг  .
. , а для емкости − отстает на
, а для емкости − отстает на  (ток опережает напряжение). Появляющийся дополнительно сдвиг фазы элемента или цепи позволяет определить время запаздывания гармонического сигнала (
(ток опережает напряжение). Появляющийся дополнительно сдвиг фазы элемента или цепи позволяет определить время запаздывания гармонического сигнала ( ), как
), как . (3.11)
. (3.11) , (3.12)
, (3.12) , (3.13)
, (3.13)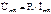 . (3.14)
. (3.14)
 . (3.15)
. (3.15) − сопротивление элемента сопротивления на гармоническом токе;
− сопротивление элемента сопротивления на гармоническом токе; − комплексное (полное) сопротивление элементов индуктивности при использовании данного метода;
− комплексное (полное) сопротивление элементов индуктивности при использовании данного метода; − комплексное (полное) сопротивление элемента емкости.
− комплексное (полное) сопротивление элемента емкости.


