
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фильтрация сигналов на фоне помехСодержание книги
Поиск на нашем сайте
Введение
В информационных системах различного назначения полезные сигналы поступают всегда на фоне помех различного происхождения. Под помехой будем понимать [1] любое воздействие на полезный сигнал, затрудняющее его прием и регистрацию. Для уверенного обнаружения полезных сигналов и измерения тех или иных их параметров необходимо обеспечить достаточное превышение энергии сигнала над энергией помех. Но при современном состоянии схемотехники информационных систем резервы повышения энергии полезного сигнала практически исчерпаны. Кроме того, некоторые помехи, например, реверберационная, растут одновременно с увеличением сигнала. Поэтому наиболее верный путь развития информационных систем заключается в оптимизации режимов обработки принимаемого сигнала с целью максимального увеличения отношения сигнал / помеха. Это может быть достигнуто прежде всего использованием фильтров с оптимальными частотными и импульсными характеристиками. Поскольку все чаще задача обнаружения полезного сигнала возлагается на автоматические устройства, очень важной оказывается также разработка оптимальных алгоритмов обнаружения и обнаружителей, реализующих эти алгоритмы. Это обосновывает необходимость изучения студентами направления «Приборостроение» вопросов обработки сигналов с учетом специфики использования соответствующих приборов и систем. ФИЛЬТРАЦИЯ СИГНАЛОВ НА ФОНЕ ПОМЕХ Постановка задачи фильтрации
Пусть на входе системы действует колебание: x (t) = F [ s (t,), n (t)], где s (t,) – полезный сигнал, n (t) – помеха, – совокупность интересующих нас параметров i (t), причем сам сигнал s (t,), или параметр i (t) – случайные процессы. Помеха n (t) может быть произвольной; сигнал и помеха не обязательно представляют собой аддитивную смесь. Считается, однако, что вид функции F (т. е. способ комбинирования сигнала и помехи) и некоторые статистические характеристики случайного сигнала и помехи нам известны. С учетом этих априорных сведений нужно решить, какая из возможных реализаций самого сигнала s (t,) или его параметра содержится в принятом колебании x (t). Из-за наличия помех и вследствие случайного характера сигнала оценка реализации сигнала или его параметра зачастую не будет совпадать с истинным значением, что приводит к ошибкам фильтрации. К тому же к фильтрам, предназначенным для использования в различных устройствах, предъявляются различные, порой противоречивые требования. Поэтому и характеристики фильтров должны удовлетворять различным критериям. Фильтры, предназначенные для устройств обнаружения, должны обеспечить максимум отношения сигнал/помеха. Фильтры, предназначенные для устройств измерения тех или иных параметров, должны отвечать критерию минимума среднеквадратической погрешности. Возможны и другие виды критериев, по которым строятся характеристики.
Согласованные фильтры
До сих пор на помеху n(t) не налагалось никаких ограничений, кроме стационарности в широком смысле. Рассмотрим теперь помеху в виде гауссовского белого шума. Линейный фильтр, на выходе которого получается максимально возможное пиковое значение отношения сигнал/помеха при приеме полностью известного сигнала на фоне гауссовского белого шума, называется согласованным фильтром. Найдем выражение для комплексной частотной характеристики согласованного фильтра. Для этого положим
(1.9) где k – постоянная, характеризующая коэффициент передачи фильтра; Es – энергия сигнала:
Запишем спектр входного сигнала и комплексную частотную характеристику фильтра в виде:
Здесь j s (w) – фазовый спектр сигнала, j(w) – фазо-частотная характеристика фильтра. Тогда выражения для амплитудно-частотной и фазочастотной характеристик согласованного фильтра будут иметь вид:
Видно, что амплитудно-частотная характеристика (АЧХ) согласованного фильтра пропорциональна амплитудному спектру входного сигнала (АЧХ фильтра «согласована» со спектром сигнала), а фазочастотная характеристика (ФЧХ) равна сумме фазочастотного спектра сигнала, взятого с обратным знаком, и фазового спектра задержки (– w t 0). Совпадение формы АЧХ фильтра с амплитудным спектром сигнала обеспечивает наилучшее выделение наиболее интенсивных участков спектра сигнала. Фильтр ослабляет участки спектра с относительно низким уровнем спектральных составляющих; в противном случае наряду с ними проходили бы интенсивные шумы. При этом форма сигнала на выходе фильтра искажается. Однако это не имеет существенного значения, так как задача фильтра в данном случае состоит не в точном воспроизведении входного сигнала, а в формировании наибольшего пика выходного сигнала на фоне шума. Существенную роль в этом отношении играет фазочастотная характеристика фильтра j (w). Подставив в формулу (1.1) выражение (1.9), получим выражение для полезного сигнала на выходе согласованного фильтра:
Отсюда видно, что сигнал на выходе фильтра определяется только амплитудным спектром входного сигнала и не зависит от его фазового спектра. Последнее обусловлено тем, что взаимные фазовые сдвиги спектральных составляющих входного сигнала js(w) компенсируются ФЧХ фильтра. Поэтому все гармонические составляющие одновременно достигают амплитудных значений в момент времени t = t 0 и, складываясь, дают пик выходного сигнала:
Если бы ФЧХ фильтра не компенсировала фазовых сдвигов спектральных составляющих входного сигнала, то максимумы гармонических составляющих не совпадали бы по времени, что привело бы к уменьшению или раздроблению пика выходного сигнала. Следует отметить, что согласованным фильтром (1.9) можно пользоваться и при приеме полностью известного сигнала на фоне стационарной помехи с произвольной спектральной плотностью Sn( w ). Для этого формально достаточно пропустить принимаемое колебание x(t) через дополнительный линейный фильтр, который преобразует помеху n(t) в белый шум. ФЧХ фильтра может быть любой, а АЧХ такого дополнительного “обеляющего” фильтра должна иметь вид:
(1.10) где На выходе обеляющего фильтра помеха превратится в белый шум с постоянной спектральной плотностью
После этого можно воспользоваться полученными ранее формулами. В соответствии с выражением (1.9) комплексная частотная характеристика соответствующего согласованного фильтра:
Оптимальный фильтр представляет собой последовательное соединение двух фильтров: обеляющего Пользуясь допустимой свободой выбора фазовой характеристики обеляющего фильтра, можно попытаться выбрать ее так, чтобы оптимальный фильтр был физически реализуем. Если спектральную плотность помехи Sn (w) можно аппроксимировать рациональной функцией частоты (что на практике не ограничивает общности), то для получения физически реализуемого оптимального линейного фильтра используют разложение Sn (w)на комплексно-сопряженные сомножители. Рассмотрим пример. Пусть помехой является гауссовский шум, имеющий спектральную плотность Sn (w)= 2a D /(a 2+ w2), где D – дисперсия шума. Тогда согласно формуле (1.10) имеем:
Таким образом, получаем два равноценных варианта обеляющих фильтров:
Найдем импульсную характеристику согласованного фильтра:
Учитывая выражение для входного сигнала:
Получаем:
Рис. 1.1 Следовательно, импульсная характеристика согласованного фильтра целиком определяется формой сигнала («согласована» с сигналом). На рис. 1.1 изображен импульсный сигнал s(t) длительностью и, появившийся в момент времени t = 0. Очевидно, что функция s(t 0 +t) появляется на время t 0 раньше, чем сигнал s(t). Функция же s(t 0 –t) является зеркальным отображением функции s(t 0 +t) относительно оси ординат. Умножив функцию s(t 0 –t) на коэффициент k, получаем импульсную характеристику согласованного фильтра.
Квазиоптимальные фильтры
При практическом построении оптимальных и согласованных линейных фильтров кроме найденных соотношений надо также учитывать условия физической возможности и практической реализуемости фильтров. Условие физической возможности фильтра записывается в виде [6]: h(t) = 0при t £0;
Если сигнал s(t), с которым должен быть согласован фильтр, начинается в момент времени 0 и полностью прекращается при t 0 + и, то первое из условий выполняется при t 0 0+и. Только при этом условии будет использована вся энергия сигнала для формирования сигнального пика на выходе фильтра в момент t 0. Увеличение t 0 сверх 0 + и, не влияя на значение пика, сдвигает его в сторону большего запаздывания, что обычно нежелательно. Поэтому следует брать t 0 = 0+и, т. е. момент наблюдения должен совпадать с окончанием входного сигнала. Иногда для аппроксимации реальных импульсных сигналов используют бесконечно длинные импульсы (гауссовский, экспоненциальный и т. д.). Тогда приходится искусственно выбирать конечное значение длительности аппроксимирующего сигнала, содержащей основную долю энергии реального сигнала. Не всякий физически возможный фильтр можно реализовать практически, т. е. построить из сравнительно небольшого числа элементов, обладающих легко выполнимыми характеристиками. В этом случае нужно либо выбирать такие сигналы, для которых получаются легко реализуемые фильтры, либо использовать практически осуществимые фильтры, отношение сигнал/помеха на выходе которых лишь немного меньше значения, определяемого соотношением (1.17). Такие фильтры называются квазиоптимальными. Обозначим через rотношение значения сигнал / помеха на выходе произвольного линейного фильтра к значению сигнал / помеха на выходе согласованного фильтра. Используя выражение (1.6) и заменяя Sn( w ) на N 0 / 2(для белого шума), получаем:
В таблице приведены максимальные значения max для различных форм полезных радиоимпульсных сигналов и разных видов частотных характеристик реализуемых фильтров при наилучших значениях их полос пропускания. При этом полоса выбирается из условия f· и = a, f – ширина полосы пропускания на уровне 0,5 по мощности, tи – эффективная длительность импульса. Видно, что уменьшение отношения сигнал/помеха при замене оптимального фильтра квазиоптимальным можно сделать весьма небольшим. При проектировании квазиоптимальных фильтров задаются структурой фильтра исходя из конструктивных соображений, а полосу его пропускания на уровне 0,707 от максимума определяют, максимизируя величину На практике часто приходится работать с сигналами, имеющими случайную амплитуду и фазу. Как следует из (1.8) и (1.9), форма частотной характеристики не зависит от амплитуды. Поэтому для сигнала со случайной амплитудой можно использовать тот же фильтр, что и для сигнала с детерминированной амплитудой. Фазочастотная характеристика фильтра зависит от фазы сигнала. Однако при непрерывном случайном изменении фазы сигнала мы в подавляющем большинстве не имеем возможности перестраивать фильтр. Поэтому случайная фаза сигнала при проектировании фильтра принимается равной своему среднему значению, что несколько снижает отношение сигнал/помеха на выходе.
Синтез оптимальных фильтров
Рассмотрим различные способы синтеза оптимальных фильтров. Фильтры для выделения сигнала на фоне коррелированного шума строятся обычно на основе спектрального метода, т. е. при использовании для комплексной частотной характеристики фильтра выражения (1.8). Для согласованных фильтров, выделяющих сигнал на фоне белого шума, возможны два метода – спектральный и временной. Временной метод основан на использовании связи между импульсной характеристикой фильтра и сигналом согласно формуле (1.11). При этом синтез согласованного фильтра заключается в построении такого линейного устройства, импульсная характеристика которого с точностью до масштабного множителя и с некоторым запаздыванием воспроизводит функцию, являющуюся зеркальным отражением сигнала. Метод особенно удобен для сигналов симметричной формы, так как в этом случае зеркальное отражение сигнала совпадает с самим сигналом. По определению импульсная характеристика есть отклик линейной системы на -функцию. Поэтому нужно так подбирать блоки согласованного фильтра, чтобы при действии на его входе d-функции на выходе воспроизводился сигнал заданной формы и длительности.
1.6.1. Синтез согласованного фильтра для прямоугольного
Рассмотрим временной и спектральный методы синтеза фильтра на примере прямоугольного видеоимпульса:
Последовательность действий при синтезе временным методом иллюстрируется рис. 1.2.
Рис. 2.2
Известно, что единичная ступенька (перепад), или функция Хевисайда Y(t), (x 2(t)) есть интеграл от -функции (x 1(t)):
После задержки единичной ступеньки на длительность импульса и (x 3(t)), ее инвертирования (x 4(t)) и вычитания из x 2(t) получим заданный прямоугольный импульс x 5(t), амплитуду которого можно изменять, меняя коэффициент передачи устройства. Отсюда следует, что искомый фильтр (рис. 1.3, а) состоит из интегратора 1, линии задержки на и 2, инвертора 3, сумматора 4 и усилителя 5. Инвертор и сумматор могут быть заменены вычитающим устройством 6 (рис. 1.3, б). Работа обоих вариантов фильтра идентична.
Рис. 1.3
Рассмотрим синтез фильтра спектральным методом. Комплексный спектр прямоугольного видеоимпульса:
Для согласованного фильтра:
Полагая и = t0, окончательно получим:
(1.18) Рассмотрим члены, входящие в выражение (1.18). Оператор Механизм работы согласованного фильтра (см. рис. 1.3) можно выяснить, рассматривая прохождение через него импульса сигнала и шума (рис. 1.4).
Рис. 1.4
Входной сигнал x1 (t)с помощью интегрирующего устройства накапливается в течение времени t и = t 0 до своего пикового значения (x 2 на рис. 1.4). Задержка на t и (x 3) и вычитание прекращают накопление сигнала, который уже дал на выходе максимальное значение, но вместе с тем прекращают и накопление шума. Выходной сигнал (x 4) становится треугольным. К аналогичному результату можно прийти, найдя аналитическое выражение для выходного полезного сигнала. Для прямоугольного видеоимпульса ковариационная функция:
или, в силу симметрии ковариационной функции: Заменяя в последнем выражении на t – t 0 и полагая и = t 0 , на основании формулы (1.14) получаем:
График этой функции совпадает с приведенным на рис. 1.4. Видно, что длительность полезного сигнала на выходе фильтра удваивается.
1.6.2. Синтез оптимального фильтра для приема прямоугольного
Пусть шум на входе фильтра имеет спектральную плотность Sn (w), отличную от равномерной:
где 2a – спектральная плотность шума при = 0; g- постоянная, характеризующая ширину энергетического спектра. В соответствии с выражением (1.8) тогда можно получить формулу для комплексной частотной характеристики оптимального фильтра для приема прямоугольного видеоимпульса на фоне коррелированного шума:
(1.19) Оператор j соответствует оператору идеального дифференцирования. Структурная схема оптимального фильтра, построенного в соответствии с формулой (1.19), изображена на рис. 1.5:
Рис. 1.5
На рисунке 6,7 – устройства дифференцирования; 8 – вычитатель. Назначение остальных блоков ясно из предыдущего. Выражение (1.19) может быть преобразовано к виду
Структурная схема фильтра, соответствующая этому выражению, содержит на один блок меньше. Временной метод синтеза оптимальных фильтров для приема сигналов на фоне коррелированного шума используется редко, так как в этом случае передаточная функция фильтра обычно не позволяет построить структурную схему столь же просто, как это было сделано ранее.
Рис. 1.7
Формальная структурная схема, поясняющая выбор критерия оптимальности фильтра, представлена на рис. 1.7. Здесь 1 – сумматор; 2 – идеальный фильтр; 3 – реальный фильтр; 4 – устройство вычисления ошибки. Пусть h(t) – импульсная характеристика реального фильтра. Тогда
и среднеквадратическая ошибка
Для стационарных сигнала и помехи Если h opt (t) – импульснаяхарактеристика оптимального фильтра, то среднеквадратическая ошибка для любого другого фильтра с импульсной характеристикой, которая представлена в виде h (t) = h opt(t)+h g (t), (1.23) может быть только больше или равна среднеквадратической ошибке оптимального фильтра. Для фильтра, имеющего характеристику, описываемую формулой (1.23), среднеквадратическая ошибка с учетом сделанных ранее обозначений
Где
Минимум
Подробно расписывая условие (1.24), получим:
Для любых g() это выражение справедливо лишь при
Отсюда видно, что импульсная характеристика оптимального фильтра может быть получена при решении интегрального уравнения (1.25). Это решение может быть получено с помощью теоремы о Фурье-преобразовании свертки. Действительно, так как интеграл в правой части есть свертка
(1.26) где F – обозначение преобразования Фурье, Sxs () – взаимная спектральная плотность принятого сообщения и сигнала; Sx () – спектральная плотность принятого сообщения; K opt(j w) – оптимальная частотная характеристика фильтра. Тогда уравнение (1.25) с учетом формул (1.26) запишется в виде
При независимых сигнале и помехе:
С учетом этих соотношений получаем:
Это решение, строго говоря, описывает физически невозможный фильтр. Однако оно имеет практический смысл, так как приближенно применимо в тех случаях и с тем большей точностью, когда можно допустить большую задержку отклика фильтра относительно входного воздействия. Поэтому говорят, что это решение пригодно для фильтров с бесконечной задержкой. Для физически возможных фильтров импульсная характеристика h(t) в силу принципа причинности существует только для t > 0, так как сигнал на выходе фильтра не может появиться раньше начала импульса на входе. Для физически возможных фильтров уравнение (1.25) приводится к виду:
т. е. к виду интегрального уравнения Винера-Хопфа, и должно решаться соответствующими методами.
НА ФОНЕ ПОМЕХ
Постановка задачи
Обнаружение сигналов практически всегда происходит при необходимости установить факт наличия или отсутствия какого-либо определенного физического объекта. Однако непосредственно установить этот факт мы обычно не можем, а можем лишь воспользоваться тем, что наличие или отсутствие интересующего нас объекта изменяет те или иные параметры некоторого сигнала – амплитуду (или сам факт наличия сигнала), время прихода, частоту, фазу и т. п. Примером может служить сигнал эхо-локационной системы, отраженный от какого-либо объекта. В этом случае сигнал присутствует лишь при наличии объекта. В других случаях объект только изменяет параметры сигнала, который присутствует все время. Общим во всех этих ситуациях является то, что сигнал поступает всегда вместе с помехами, а это может привести к ошибочным решениям. Случайный характер как помех, так и полезных сигналов приводит к тому, что при решении задачи обнаружения следует исходить из положений теории статистических решений.
Рис. 2.4
Участок под кривой pn(x) справа от x 0 определяет условную вероятность ложной тревоги, под кривой psn(x) – условную вероятность правильного обнаружения. При смещении кривой psn(x) вправо, что соответствует увеличению сигнала s, вероятность правильного обнаружения возрастает. Структурная схема простейшего обнаружителя Неймана-Пирсона состоит из одного блока – порогового устройства. На первый вход его подается входной сигнал x(t), на второй вход – пороговое значение x 0. Сравнивая значения x(t) c x0, пороговое устройство в каждый момент времени вырабатывает решение о наличии или отсутствии сигнала.
Рис. 2.11
Она состоит из согласованного фильтра 1, детектора огибающей 2 и порогового устройства 3. Детектор выполняет функцию выделения огибающей. Характеристики обнаружения такого обнаружителя могут быть определены по формулам (2.17) и (2.18).
И начальной фазой
При работе систем обнаружения слабых сигналов, как правило, приходится иметь дело с сигналами, имеющими случайные значения амплитуд и начальных фаз. Такие сигналы можно записать в виде:
где B и – случайные амплитудный множитель и фаза с плотностями распределения:
Аналогично предыдущему, корреляционный интеграл можно представить в виде двух квадратурных составляющих:
Следует отметить, что B – медленно изменяющаяся величина, практически постоянная в интервале [0 ,T ]. Корреляционный интеграл тогда равен Энергия флуктуирующего сигнала будет равна:
(2.19) где
Тогда Используя выражения (2.14) и (2.19), можно записать отношение правдоподобия в виде:
Теперь необходимо усреднить это выражение по случайным параметрам B и:
Схема оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой не отличается от схемы оптимального обнаружителя сигнала со случайной фазой. По-прежнему оптимальной является квадратурная схема обработки. Плотность распределения вероятностей при отсутствии сигнала, как и ранее, описывается законом Рэлея:
В случае наличия сигнала на входе устройства закон распределения также будет рэлеевским, но с плотностью распределения:
Это следует из того, что вследствие независимости сигнала и помехи Тогда условная вероятность ложной тревоги:
(2.20) При обнаружении по стратегии Неймана-Пирсона:
(2.21) Условная вероятность правильного обнаружения:
(2.22) Здесь: Подставляя сюда выражение (2.21), можно получить:
(2.23) Выражение (2.23) устанавливает связь между условными вероятностями ложной тревоги и правильного обнаружения. Кривые обнаружения, рассчитанные по формулам (2.20) и (2.22), приведены на рис. 2.6 (штрихпунктирные линии). Из рисунка видно, что при увеличении отношения сигнал/помеха все кривые сначала растут медленно, а потом быстрее. При больших вероятностях правильного обнаружения кривые для сигнала со случайной начальной фазой и особенно для сигнала со случайными амплитудой и фазой смещены в сторону больших значений отношения сигнал/помеха. Наоборот, при малых вероятностях правильного обнаружения (PD 0,2) кривые обнаружения для сигнала со случайными амплитудой и фазой идут выше соответствующих кривых для других двух сигналов. Это объясняется тем, что при равенстве энергий амплитуда сигнала со случайными амплитудой и фазой с вероятностью Р = 0,74будет превышать амплитуду сигнала с полностью известными параметрами [8]. Значительно проще структурная схема оптимального обнаружителя с согласованным фильтром (рис. 2.11). Характеристики обнаружения такого обнаружителя могут быть определены в соответствии с выражениями (2.20)–(2.23). Однако в ряде случаев удобнее оказывается использовать несколько иной подход. Как указывалось ранее, случайные сигналы (и помехи) на выходе согласованного фильтра обычно можно считать распределенными по гауссовскому закону. При этом на выходе согласованного фильтра можно измерить дисперсии (или пропорциональные им мощности) помехи
Вероятность ложной тревоги:
Отсюда пороговое значение:
Аналогично, вероятность правильного обнаружения:
или
где Из изложенного видно, что оптимальные обнаружители на базе согласованных фильтров, имея те же характеристики обнаружения, что и корреляционные обнаружители, зачастую оказываются проще в реализации, так как не требуют наличия копии сигнала, задержанной на время распространения.
Постановка задачи
До сих пор мы рассматривали обнаружение сигнала от объекта в одной точке наблюдения. Однако на практике при сканировании пространства сигналы от того или иного объекта обычно поступают в течение некоторого времени: поступает пачка сигналов. Это вызывается, во-первых, конечной протяженностью большинства реальных объектов. Во-вторых, конечные размеры имеет также участок пространства, с которого в данный момент снимается информация о наличии или отсутствии объекта. Размеры этого участка зависят от размеров приемника. В результате при не слишком большом шаге сканирования мы зачастую имеем пачку сигналов конечной длительности, состоящую из нескольких сигналов одинаковой или различной амплитуды, либо (например, при непрерывном излучении) один сигнал большой длительности. Это явление целесообразно использовать для обнаружения сигналов, так как оно позволяет значительно увеличить чувствительность и достоверность обнаружения. Задача обнаружения пачки сигналов будет решаться по-разному в зависимости от свойств такой пачки. Если зависимость между всеми параметрами импульсов, входящих в пачку, полностью известна, то такие импульсы и такая пачка называются когерентными. В противном случае пачка называется некогерентной. Когерентная пачка импульсов с полностью известными параметрами является частным случаем полностью известного сигнала, и для нее справедливы выражения (2.15) и (2.16), если в них под энергией сигнала понимать сумму энергий всех импульсов пачки. Зачастую при обнаружении объектов импульсные сигналы в пачке флуктуируют. Эти флуктуации могут быть полностью коррелированными, частично коррелированными и некоррелированными. В первом случае сигналы флуктуируют от пачки к пачке, но соотношение параметров отдельных импульсов между собой от пачки к пачке не меняется: форма пачки одна и та же. Такие флуктуации носят название «дружных». Дружно флуктуирующую пачку можно рассматривать как одиночный сигнал сложной формы со случайными амплитудой и фазой. В случае некоррелированных флуктуаций амплитуды и начальные фазы отдельных и
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 Тогда выражения (1.7) и (1.8) примут соответственно вид:
Тогда выражения (1.7) и (1.8) примут соответственно вид:




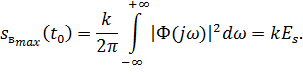

 – постоянная.
– постоянная.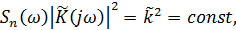 а комплексный спектр сигнала будет:
а комплексный спектр сигнала будет:

 и согласованного
и согласованного  . Его комплексная частотная характеристика
. Его комплексная частотная характеристика 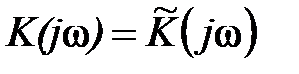
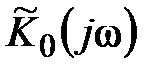 естественно совпадает с соотношением (1.8).
естественно совпадает с соотношением (1.8).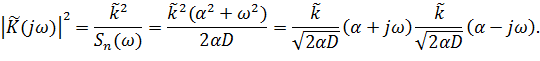
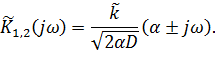




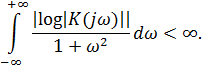

 при изменении полосы пропускания. Квазиоптимальные фильтры для радиоимпульсных и вообще для высокочастотных сигналов выполняются на базе колебательных контуров или активных полосовых фильтров. Число контуров обычно задается из конструктивных соображений. Полосу пропускания оптимизируют, изменяя добротность колебательной системы.
при изменении полосы пропускания. Квазиоптимальные фильтры для радиоимпульсных и вообще для высокочастотных сигналов выполняются на базе колебательных контуров или активных полосовых фильтров. Число контуров обычно задается из конструктивных соображений. Полосу пропускания оптимизируют, изменяя добротность колебательной системы.



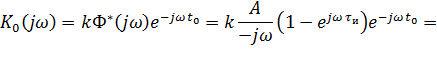


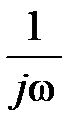 , как известно, представляет собой оператор идеального интегрирования гармонического сигнала; kA – коэффициент передачи линейного устройства;
, как известно, представляет собой оператор идеального интегрирования гармонического сигнала; kA – коэффициент передачи линейного устройства;  – задержку на время t и. Видно, что структурная схема такого фильтра соответствует рис. 1.3.
– задержку на время t и. Видно, что структурная схема такого фильтра соответствует рис. 1.3.

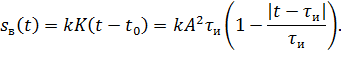





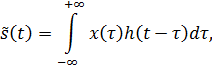

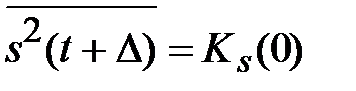 – максимальное значение ковариационной функции сигнала;
– максимальное значение ковариационной функции сигнала;  – взаимная ковариационная функция принятой реализации и сигнала;
– взаимная ковариационная функция принятой реализации и сигнала;  – ковариационная функция принятой реализации.
– ковариационная функция принятой реализации.





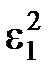 может быть найден из условия
может быть найден из условия (1.24)
(1.24)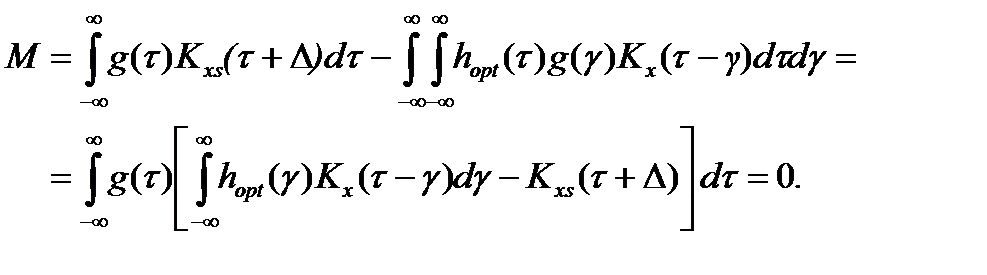
 . (1.25)
. (1.25) , то, взяв преобразование Фурье от левой и правой частей этого уравнения, получим:
, то, взяв преобразование Фурье от левой и правой частей этого уравнения, получим:
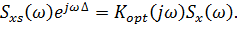


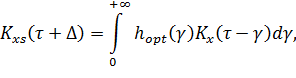
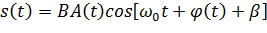

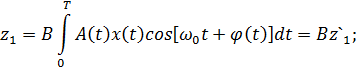

 , где
, где  .
.
 – энергия нефлуктуирующего сигнала при B = 1. Отсюда можно определить
– энергия нефлуктуирующего сигнала при B = 1. Отсюда можно определить  , усреднив (2.19) по B:
, усреднив (2.19) по B:
 =1/ 2 и
=1/ 2 и 



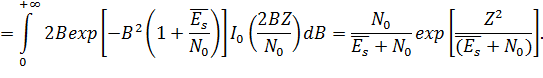


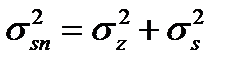 , где
, где 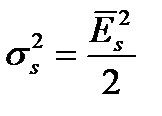 – дисперсия сигнальной составляющей корреляционного интеграла.
– дисперсия сигнальной составляющей корреляционного интеграла.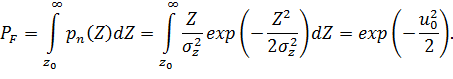

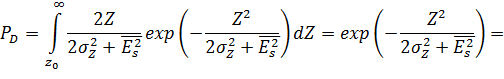

 .
.
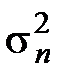 и смеси сигнала с помехой
и смеси сигнала с помехой  . Для наиболее распространенного случая независимости сигнала и помехи
. Для наиболее распространенного случая независимости сигнала и помехи  , где
, где  – дисперсия полезного сигнала. Тогда на выходе детектора помеха и смесь сигнала с помехой будут распределены по закону Рэлея:
– дисперсия полезного сигнала. Тогда на выходе детектора помеха и смесь сигнала с помехой будут распределены по закону Рэлея:
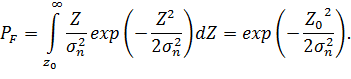




 . Нетрудно убедиться, что
. Нетрудно убедиться, что 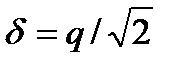 , поскольку в выражение для q входит максимальное значение сигнала, а в – его среднеквадратическое значение.
, поскольку в выражение для q входит максимальное значение сигнала, а в – его среднеквадратическое значение.


