
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обнаружение коррелированных сигналовСодержание книги
Поиск на нашем сайте
В ряде случаев помехи бывают связаны с неинформативными параметрами исследуемого объекта. Примерами таких помех являются реверберация в море и в металле, отражения от структурных неоднородностей тканей человеческого тела (кровеносные сосуды и т. п.). При ультразвуковом контроле это, например, помехи, связанные с шероховатостью и загрязнениями поверхности контролируемых изделий, и т. д. В результате увеличение длительности контроля одной и той же точки изделия, например посылка нескольких импульсов при одном и том же положении датчика, не приводит к повышению отношения сигнал/помеха, так как помеха, как и значение полезного сигнала, жестко связаны с положением датчика относительно изделия. В этом случае накопление эффективно при движении датчика относительно объекта, если полезный сигнал может быть зарегистрирован не в одной точке, а на протяжении некоторого отрезка линии сканирования, и помеха при таком перемещении датчика флуктуирует. Тогда совокупность сигналов на выходе приемного датчика при его движении можно рассматривать как реализацию случайного процесса x(t). (При импульсном характере работы рассматривается огибающая амплитуд принимаемых импульсов.) Рассмотрим пересечение стационарного дифференцируемого процесса x(t) с постоянным уровнем C. Согласно [6], среднее число выбросов этого процесса за уровень C:
где
Для дальнейшего решения задачи необходимо задаться видом двухмерной плотности, т. е. видом закона распределения сигнала x(t). Рассмотрим случай ультразвукового теневого контроля стальных горячекатаных изделий. Как показывают эксперименты [12], [13], в этом случае закон распределения огибающей амплитуд U(t) можно считать гауссовским. Учитывая, что при теневом контроле на бездефектном участке среднее значение амплитуд должно быть выше порога, можно получить, что интенсивность ложной тревоги (перебраковки), т. е. среднее количество выбросов – ложных регистраций дефектов на единицу длины пути сканирования:
Если в изделии имеется протяженный дефект с акустической прозрачностью T, то на дефектном участке интенсивность пропуска цели (недобраковки), т. е. среднее количество пропусков в регистрации дефектов,
Здесь mU – среднее значение огибающей амплитуд на бездефектном участке контролируемого изделия; Вводя в двух последних выражениях нормировку по уровню среднего значения, получим:
(3.7)
(3.8) Здесь
(3.9)
(3.10) Приравнивая правые части выражений (3.9) и (3.10), можно записать выражение для максимальной акустической прозрачности T max протяженного дефекта, который выявляется с заданной надежностью (заданными
Взаимное расположение огибающей амплитуд и порогового уровня на бездефектном и дефектном участках показаны на рис. 3.4.
Рис. 3.4
Проведенное рассмотрение справедливо для случая, когда необходимо учитывать лишь одномерные корреляционные связи огибающих амплитуд сигналов. Однако при контроле изделия по всей его площади при бесконечно малом шаге сканирования совокупность результатов контроля можно рассматривать как реализацию случайного поля амплитуд, что требует учета двухмерных корреляционных связей. Соответствующее рассмотрение на основе теории выбросов случайных полей проведено в [14] без учета и с учетом конечности значения шага сканирования в продольном и поперечном направлениях. Приведенные там же результаты расчетов показали, что в большинстве случаев для реальных параметров сканирования можно пренебречь корреляционными связями сигналов в одном направлении и рассчитывать чувствительность и надежность контроля по приведенным ранее формулам.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.96 (0.005 с.) |


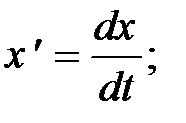
 ;
; 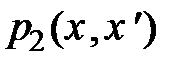 – двухмерная плотность вероятностей ординаты случайного процесса x(t) и его производной; L – длина реализации. Интенсивность выбросов, т. е. количество выбросов на единицу длительности,
– двухмерная плотность вероятностей ординаты случайного процесса x(t) и его производной; L – длина реализации. Интенсивность выбросов, т. е. количество выбросов на единицу длительности,

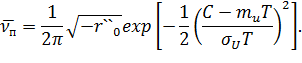
 – дисперсия огибающей амплитуд;
– дисперсия огибающей амплитуд;  – значение второй производной нормированной корреляционной функции огибающей амплитуд
– значение второй производной нормированной корреляционной функции огибающей амплитуд  в точке = 0.
в точке = 0.

 – коэффициент вариации огибающей амплитуд. Формулы (3.7) и (3.8) позволяют получить выражения для относительного порога регистрации u:
– коэффициент вариации огибающей амплитуд. Формулы (3.7) и (3.8) позволяют получить выражения для относительного порога регистрации u:
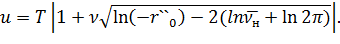
 ):
):



