
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности обнаружения изменений параметров сигналаСодержание книги
Поиск на нашем сайте
Статистическая теория обнаружения сигналов на фоне помех была первоначально разработана для целей поиска малых сигналов в радиолокации, а впоследствии полученные результаты были распространены на задачи гидролокации, эхо-импульсной дефектоскопии и т. д. Во всех этих областях имеется сходство в формулировке задачи: с некоторой вероятностью, зачастую априорно неизвестной, появляется полезный сигнал, который и нужно обнаружить на фоне различного рода помех. Основные идеи теории обнаружения могут быть распространены и на задачи просвечивания: теневой метод дефектоскопии, медицинского рентгеновского просвечивания и т. п. Особенностью методов просвечивания является то, что сигнал имеется и в отсутствие интересующих нас объектов в контролируемой среде. Наличие выявляемого объекта изменяет те или иные параметры сигнала (чаще всего амплитуду и время прихода) ([10], [11]). Параметры эти могут изменяться и под влиянием каких-то мешающих воздействий. При этом необходимо выявить только те изменения информативного параметра, которые вызваны наличием объекта. Этот подход может быть распространен и на все ситуации, когда сигнал, приходящий на фоне помех, присутствует постоянно, и нам необходимо обнаруживать изменения тех или иных его параметров, вызванные какими-то внешними воздействиями. Рассмотрим задачу более подробно на примере теневого амплитудного дефектоскопа. Наличие дефекта в контролируемом изделии приводит к изменению амплитуды принимаемого сигнала. В ультразвуковых дефектоскопах амплитуда принимаемого сигнала на дефектных участках практически всегда уменьшается, в радиационных дефектоскопах дефект может как увеличивать уровень принимаемого сигнала (дефект – включения из материалов более легких, чем материал изделия), так и уменьшать его (дефект – включения из материалов более тяжелых, чем материал изделия).
Рис. 2.13
Пусть металлическое изделие 4, погруженное в жидкость 3 (рис. 2.13), контролируется теневым ультразвуковым дефектоскопом. Из-за небольших изменений затухания ультразвуковых колебаний в материале изделия, рассеяния их на неровностях поверхностей изделия и ослабления из-за остаточных загрязнений и ряда других причин амплитуда прошедшего ультразвукового сигнала при перемещении излучающего 1 и приемного 2 преобразователей вдоль поверхности изделия все время флуктуирует. Закон распределения амплитуд U прошедших сигналов на бездефектном участке изделия может быть описан плотностью распределения вероятностей p(U). Наличие протяженного звукопрозрачного дефекта 5 с акустической прозрачностью T (T < 1) соответственно изменит в T раз амплитуды всех сигналов на этом участке. Плотность распределения вероятностей амплитуд преобразуется в pT(U), как показано на рис. 2.14. При этом вид закона распределения останется прежним, а математическое ожидание и среднеквадратическое отклонение изменятся в T раз. При контроле амплитуда прошедшего сигнала сравнивается с порогом U 0. Если она меньше порога, принимается решение о наличии дефекта, если больше – о его отсутствии. Таким образом, порядок принятия решения здесь обратен тому, который был описан ранее. При этом условные вероятности равны:
Рис. 2.14
Если известен закон распределения, то из формул (2.24)–(2.26) можно получить конкретные соотношения, позволяющие связать значения рабочего порога с характеристиками флуктуаций и надежностью контроля. Некоторые результаты расчетов изложены в [12]. Если по условиям задачи отслеживаемое изменение параметра исследуемого объекта или явления вызывает не уменьшение, а увеличение амплитуды сигнала, то пределы интегрирования в формулах (2.24)–(2.26) соответственно изменятся.
ОБНАРУЖЕНИЕ ПРОТЯЖЕННЫХ ОБЪЕКТОВ
Постановка задачи
До сих пор мы рассматривали обнаружение сигнала от объекта в одной точке наблюдения. Однако на практике при сканировании пространства сигналы от того или иного объекта обычно поступают в течение некоторого времени: поступает пачка сигналов. Это вызывается, во-первых, конечной протяженностью большинства реальных объектов. Во-вторых, конечные размеры имеет также участок пространства, с которого в данный момент снимается информация о наличии или отсутствии объекта. Размеры этого участка зависят от размеров приемника. В результате при не слишком большом шаге сканирования мы зачастую имеем пачку сигналов конечной длительности, состоящую из нескольких сигналов одинаковой или различной амплитуды, либо (например, при непрерывном излучении) один сигнал большой длительности. Это явление целесообразно использовать для обнаружения сигналов, так как оно позволяет значительно увеличить чувствительность и достоверность обнаружения. Задача обнаружения пачки сигналов будет решаться по-разному в зависимости от свойств такой пачки. Если зависимость между всеми параметрами импульсов, входящих в пачку, полностью известна, то такие импульсы и такая пачка называются когерентными. В противном случае пачка называется некогерентной. Когерентная пачка импульсов с полностью известными параметрами является частным случаем полностью известного сигнала, и для нее справедливы выражения (2.15) и (2.16), если в них под энергией сигнала понимать сумму энергий всех импульсов пачки. Зачастую при обнаружении объектов импульсные сигналы в пачке флуктуируют. Эти флуктуации могут быть полностью коррелированными, частично коррелированными и некоррелированными. В первом случае сигналы флуктуируют от пачки к пачке, но соотношение параметров отдельных импульсов между собой от пачки к пачке не меняется: форма пачки одна и та же. Такие флуктуации носят название «дружных». Дружно флуктуирующую пачку можно рассматривать как одиночный сигнал сложной формы со случайными амплитудой и фазой. В случае некоррелированных флуктуаций амплитуды и начальные фазы отдельных импульсов пачки меняются случайным образом вне связи друг с другом. Зачастую наибольший интерес представляет именно этот случай, а также случай частично коррелированных флуктуаций в пачке. При этом обнаружитель обычно состоит из оптимального фильтра для одиночного сигнала и устройства обработки пачки сигналов.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

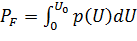 – ложная тревога, (2.24)
– ложная тревога, (2.24) – пропуск цели, (2.25)
– пропуск цели, (2.25) – правильное обнаружение. (2.26)
– правильное обнаружение. (2.26)


