
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обнаружение сигнала со случайной начальной фазойСодержание книги
Поиск на нашем сайте
Рассмотрим обнаружение сигнала, имеющего детерминированную амплитуду и случайную начальную фазу высокочастотного заполнения. Будем считать, что плотность распределения вероятностей фазы равномерна в интервале 0...2p: p (b) = 1/2p. Отношение правдоподобия в этом случае будет еще и функцией фазы b. Энергия сигнала мало зависит от b, поэтому считаем ее постоянной. Пусть полезный сигнал имеет вид:
где A(t) – детерминированный амплитудный множитель; j (t) – детерминированный фазовый множитель; – случайный фазовый множитель. Тогда выражение для корреляционного интеграла будет:
Введем обозначения:
Тогда
где Подставим эту формулу в выражение (2.14) для отношения правдоподобия полностью известного сигнала:
Это выражение является случайной функцией. Поэтому в нем необходимо произвести усреднение по. Тогда:
Но, по определению,
где I0(x) – модифицированная функция Бесселя нулевого порядка. Окончательно:
Это отношение правдоподобия является монотонной функцией огибающей корреляционного сигнала Z. Поэтому оптимальным правилом обнаружения является вычисление значения Z и сравнение его с порогом Z 0. Если Z > Z 0, сигнал есть, если Z < Z 0, сигнала нет. Структурная схема обнаружителя, включающая два квадратурных канала, представлена на рис. 2.9.
Рис. 2.9
В каждом канале вычисляются квадратурные составляющие корреляционного интеграла z 1 и z 2 соответственно. Затем находится огибающая Z, которая сравнивается с порогом Z 0, устанавливаемым в соответствии с выбранным критерием оптимальности. В качестве опорных напряжений для умножителей используются сдвинутые по фазе на p /2 колебания высокой частоты:
Для расчета кривых обнаружения необходимо найти законы распределения величины Z при наличии и отсутствии сигнала. Случайные величины z 1 и z 2 не коррелированы и распределены по гауссовскому закону. Тогда при отсутствии сигнала на входе плотность распределения вероятностей Z описывается законом Рэлея:
При наличии сигнала на входе плотность распределения вероятностей Z описывается обобщенным законом Рэлея:
Из теории распределения Рэлея известно, что:
Тогда условная вероятность ложной тревоги:
(2.17) При работе обнаружителя по критерию Неймана-Пирсона из выражения (2.17) может быть определен порог регистрации
Условная вероятность правильного обнаружения:
(2.18) где Определяемая отсюда величина условной вероятности правильного обнаружения PD может быть найдена по таблицам функции распределения обобщенного закона Рэлея (закона Рэлея-Райса) либо численным интегрированием. Результаты расчетов по выражениям (2.17) и (2.18) приведены на рис. 2.6 (штриховые линии). Примерная картина плотностей распределения на входе порогового устройства приведена на рис. 2.10.
Рис. 2.10
Значительно проще структурная схема оптимального обнаружителя с согласованным фильтром (рис. 2.11):
Рис. 2.11
Она состоит из согласованного фильтра 1, детектора огибающей 2 и порогового устройства 3. Детектор выполняет функцию выделения огибающей. Характеристики обнаружения такого обнаружителя могут быть определены по формулам (2.17) и (2.18).
Обнаружение сигнала со случайными амплитудой И начальной фазой
При работе систем обнаружения слабых сигналов, как правило, приходится иметь дело с сигналами, имеющими случайные значения амплитуд и начальных фаз. Такие сигналы можно записать в виде:
где B и – случайные амплитудный множитель и фаза с плотностями распределения:
Аналогично предыдущему, корреляционный интеграл можно представить в виде двух квадратурных составляющих:
Следует отметить, что B – медленно изменяющаяся величина, практически постоянная в интервале [0 ,T ]. Корреляционный интеграл тогда равен Энергия флуктуирующего сигнала будет равна:
(2.19) где
Тогда Используя выражения (2.14) и (2.19), можно записать отношение правдоподобия в виде:
Теперь необходимо усреднить это выражение по случайным параметрам B и:
Схема оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой не отличается от схемы оптимального обнаружителя сигнала со случайной фазой. По-прежнему оптимальной является квадратурная схема обработки. Плотность распределения вероятностей при отсутствии сигнала, как и ранее, описывается законом Рэлея:
В случае наличия сигнала на входе устройства закон распределения также будет рэлеевским, но с плотностью распределения:
Это следует из того, что вследствие независимости сигнала и помехи Тогда условная вероятность ложной тревоги:
(2.20) При обнаружении по стратегии Неймана-Пирсона:
(2.21) Условная вероятность правильного обнаружения:
(2.22) Здесь: Подставляя сюда выражение (2.21), можно получить:
(2.23) Выражение (2.23) устанавливает связь между условными вероятностями ложной тревоги и правильного обнаружения. Кривые обнаружения, рассчитанные по формулам (2.20) и (2.22), приведены на рис. 2.6 (штрихпунктирные линии). Из рисунка видно, что при увеличении отношения сигнал/помеха все кривые сначала растут медленно, а потом быстрее. При больших вероятностях правильного обнаружения кривые для сигнала со случайной начальной фазой и особенно для сигнала со случайными амплитудой и фазой смещены в сторону больших значений отношения сигнал/помеха. Наоборот, при малых вероятностях правильного обнаружения (PD 0,2) кривые обнаружения для сигнала со случайными амплитудой и фазой идут выше соответствующих кривых для других двух сигналов. Это объясняется тем, что при равенстве энергий амплитуда сигнала со случайными амплитудой и фазой с вероятностью Р = 0,74будет превышать амплитуду сигнала с полностью известными параметрами [8]. Значительно проще структурная схема оптимального обнаружителя с согласованным фильтром (рис. 2.11). Характеристики обнаружения такого обнаружителя могут быть определены в соответствии с выражениями (2.20)–(2.23). Однако в ряде случаев удобнее оказывается использовать несколько иной подход. Как указывалось ранее, случайные сигналы (и помехи) на выходе согласованного фильтра обычно можно считать распределенными по гауссовскому закону. При этом на выходе согласованного фильтра можно измерить дисперсии (или пропорциональные им мощности) помехи
Вероятность ложной тревоги:
Отсюда пороговое значение:
Аналогично, вероятность правильного обнаружения:
или
где Из изложенного видно, что оптимальные обнаружители на базе согласованных фильтров, имея те же характеристики обнаружения, что и корреляционные обнаружители, зачастую оказываются проще в реализации, так как не требуют наличия копии сигнала, задержанной на время распространения.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.011 с.) |



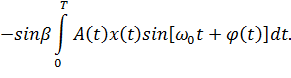

 . Найдем огибающую Z и фазу корреляционного интеграла:
. Найдем огибающую Z и фазу корреляционного интеграла:  . Тогда корреляционный интеграл запишется в виде:
. Тогда корреляционный интеграл запишется в виде:











 :
:
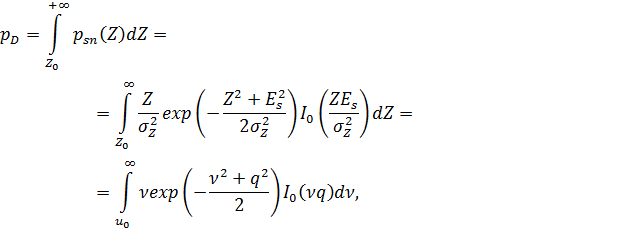
 .
.
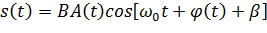

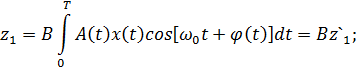

 , где
, где  .
.
 – энергия нефлуктуирующего сигнала при B = 1. Отсюда можно определить
– энергия нефлуктуирующего сигнала при B = 1. Отсюда можно определить  , усреднив (2.19) по B:
, усреднив (2.19) по B:
 =1/ 2 и
=1/ 2 и 



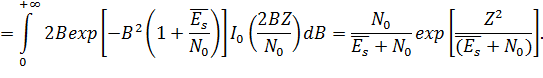


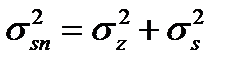 , где
, где 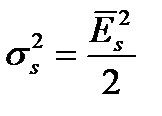 – дисперсия сигнальной составляющей корреляционного интеграла.
– дисперсия сигнальной составляющей корреляционного интеграла.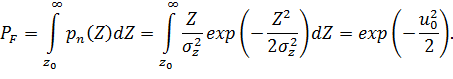

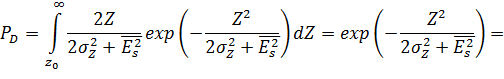

 .
.
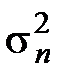 и смеси сигнала с помехой
и смеси сигнала с помехой  . Для наиболее распространенного случая независимости сигнала и помехи
. Для наиболее распространенного случая независимости сигнала и помехи  , где
, где  – дисперсия полезного сигнала. Тогда на выходе детектора помеха и смесь сигнала с помехой будут распределены по закону Рэлея:
– дисперсия полезного сигнала. Тогда на выходе детектора помеха и смесь сигнала с помехой будут распределены по закону Рэлея:
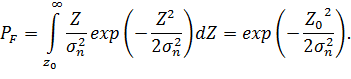




 . Нетрудно убедиться, что
. Нетрудно убедиться, что 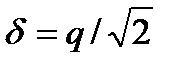 , поскольку в выражение для q входит максимальное значение сигнала, а в – его среднеквадратическое значение.
, поскольку в выражение для q входит максимальное значение сигнала, а в – его среднеквадратическое значение.


