Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач оптимизации данных .Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Материальное обеспечение: компьютерный класс № 412 с набором оборудования для проведения лабораторных занятий. Теоретический материал Решение задач оптимизации данных Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.). В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения». Пример решения задачи Задача определения оптимального ассортимента продукции
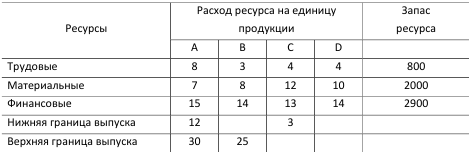
Предприятие изготавливает четыре вида продукции – A, B, C и D. Для производства продукции используются ресурсы – трудовые, материальные, финансовые. Максимальный запас ресурсов на производстве 800, 2000, 2900 соответственно. Расход ресурсов на единицу производства продукции A, B, C и D и предельно допустимые значения выпуска каждого вида даны в таблице.
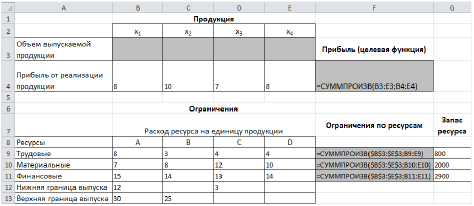
Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. – для B, 7 д. е. – для C, 8 д. е. – для D. Какой объем продукции каждого вида должно производить предприятие, чтобы прибыль от реализации продукции была максимальной? Решение. Составим математическую модель для решения поставленной задачи. Обозначим переменные: x1 – объем произведенной продукции вида А; x2 – объем произведенной продукции вида B; x3 – объем произведенной продукции вида C; x4 – объем произведенной продукции вида D; Поскольку производство продукции ограничено имеющимися в распоряжении предприятия ресурсами и спросом на данную продукцию, а также учитывая, что объем изготовляемой продукции не может быть отрицательным, должны выполняться следующие неравенства:
Прибыль от реализации продукции составит: Cреди всех неотрицательных решений системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение Fmax. Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также использованы прибыль, себестоимость, номенклатура производимой продукции, затраты станочного времени и др. Создадим на рабочем листе таблицу для ввода исходных данных. Заливкой выделены ячейки для ввода формул и вывода результата.
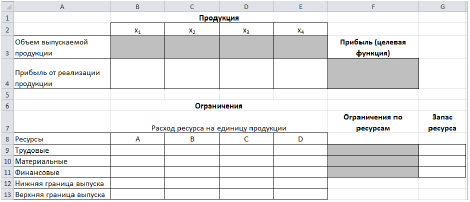
Рис.1 Заполним таблицу. Блок ячеек В3:Е3 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи. Блок ячеек В4:Е4 содержит значения прибыли от реализации продукции. В ячейках В9: Е13 отображен расход ресурсов на единицу производства продукции A, B, C и D и предельно допустимые значения выпуска каждого вида. Для вычисления целевой функции в ячейке F4 используем функцию =СУММПРОИЗВ(B3:E3;B4:E4) (рис. 2).
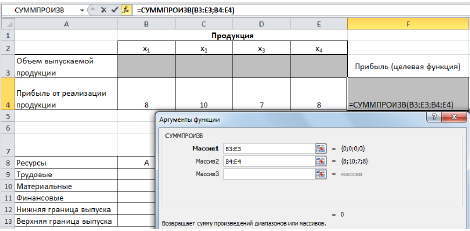
Рис. 2 В ячейки F9:F11 введены формулы для расчета ограничений по ресурсам. На рис. 2.3 представлена таблица с исходными данными, целевой функцией, ограничениями и граничными условиями.
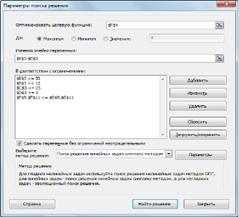
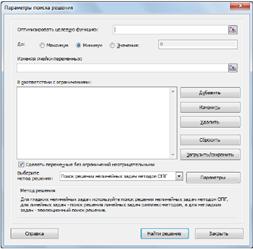
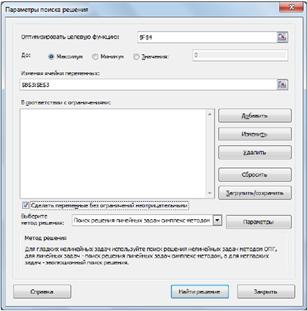
Рис. 3 На вкладке Данные в группе Анализ выберем команду Поиск решения. На экране отобразится диалоговое окно Параметры поиска решения, в котором установим следующие параметры: в поле Оптимизировать целевую функцию указываем адрес ячейки со значением целевой функции – F4; выбираем нахождение максимума целевой функции; в поле Изменяя ячейки переменных указываем адреса ячеек со значениями искомых переменных B3:Е3; в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения задачи (добавление ограничений будет рассмотрено ниже); установим флажок в поле Сделать переменные без ограничений неотрицательными; в списке Выберите метод решения указываем Поиск решения линейных задач симплекс-методом; нажимаем кнопку Найти решение.
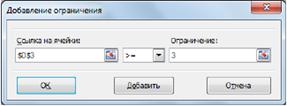
Рис. 4 Остановимся подробно на добавлении ограничений в область В соответствии с ограничениями. Все ограничения указаны в системе (2.5). Для добавления ограничения необходимо выбрать кнопку Добавить. Отобразится окно диалога Добавление ограничений. Добавляем ограничения для неравенств:
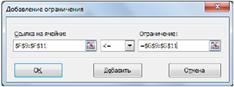
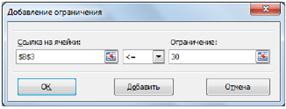
В поле Ссылка на ячейки указываем адрес диапазона F9:F11, выбираем в раскрывающемся списке знак неравенства ≤, в поле Ограничение выделяем диапазон G9:G11 и нажимаем кнопку Добавить (рис. 2.5). Результатом этого действия будет добавление текущего ограничения в список ограничений, поля окна Добавление ограничения будут очищены для ввода следующего ограничения. Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.
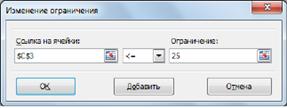
Рис. 5 Покажем окна для добавления остальных ограничений.
Рис. 6
Рис. 7
Рис. 8
Рис. 9 Ограничения Для принятия последнего ограничения и возврата к диалоговому окну Параметры поиска решения нажмем кнопку OK. После указания всех необходимых параметров в диалоговое окно Параметры поиска решения примет вид:
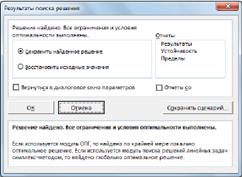
Рис. 10 После выбора кнопки Найти решение отобразится окно Результаты поиска решения:
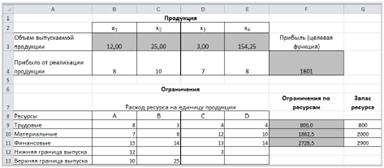
Рис. 11 Для сохранения полученного решения необходимо установить переключатель Сохранить найденное решение и нажать кнопку ОК. После чего на рабочем листе отобразится решение задачи:
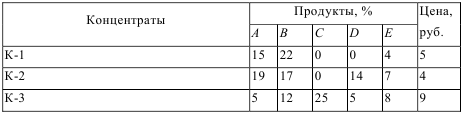
Рис. 12 Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1601 д. е. при следующем плане производства: 12,00 – объем продукции типа А; 25,00 – объем продукции типа B; 3,00 – объем продукции типа C; 124,25– объем продукции типа D; Практическое задание 1: Решить задачи оптимизации данных. 1. Рацион стада оленей из 220 голов включает пищевые продукты А, В, С, D и Е. В сутки одно животное должно съедать не менее 2 кг продукта вида А, 1,5 кг продукта В, 0,9 кг продукта С, 3 кг продукта D и 1,8 кг продукта Е. Однако в чистом виде указанные продукты не производятся. Они содержатся в концентратах К-1, К-2, К-3. Их цена и содержание продуктов (в процентах) приведены в таблице.
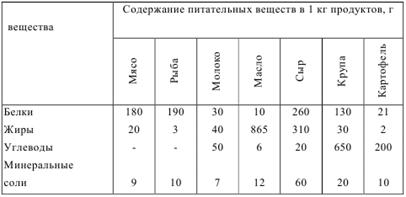
Минимизировать затраты на покупку концентратов при рациональном кормлении скота. 2. Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в 1 кг каждого вида потребляемых продуктов, а также цена 1 кг каждого из этих продуктов приведены в таблицах.
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 2294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.008 с.) |

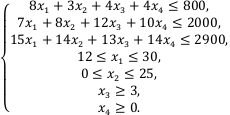
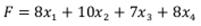
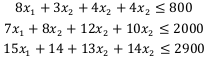
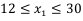 .
.
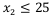
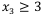
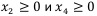 можно не добавлять, т.к. в окне Параметры поиска решения установлен флажок в поле Сделать переменные без ограничений неотрицательными.
можно не добавлять, т.к. в окне Параметры поиска решения установлен флажок в поле Сделать переменные без ограничений неотрицательными.