
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели задачи фирмыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим оптимизационные модели производства. При этом будем моделировать не само производство, как таковое, а задачу принятия решения относительно планирования производства. Поэтому будем предполагать выполненными следующие аксиомы: 1. любое производство начинается с этапа планирования; 2. принимаются только реалистичные планы; 3. принятые планы выполняются. На основе этих положений задача фирмы как организации, производящей затраты производственных ресурсов для изготовления товаров, сводится к определению количества выпускаемой продукции и необходимых для этого затрат. Фирма должна решить свою задачу наилучшим (т.е. оптимальным) образом. При этом оптимальность можно понимать двояко: либо как получение наибольшей прибыли (с учетом имеющихся возможностей фирмы относительно затрат ресурсов), либо как достижение необходимого (фиксированного) уровня выпуска с наименьшими затратами. Фирма может поставить перед собой только одну из этих целей. В противном случае задача будет некорректной, т.е. нереализуемой. Действительно, нельзя осуществить наибольший выпуск при наименьших затратах. В теории многокритериальной оптимизации этот факт устанавливается строго. С точки зрения временного промежутка (горизонта планирования) можно различить задачи двух типов - задачу текущего производства (краткосрочная задача) и задачу перспективного развития (долгосрочная задача). Краткосрочная задача ставится на один производственный цикл - от начала производства товара до момента выхода фирмы со своим товаром на рынок. Здесь решается задача рационального использования уже имеющихся в распоряжении фирмы ресурсов, производственных мощностей, сырья, расходов на заработную плату. Поэтому математические модели краткосрочной задачи фирмы представляют собой оптимизационные задачи с ограничениями. Долгосрочная задача охватывает период, достаточный для принятия и реализации крупномасштабных решений: наращивания или сокращения основных фондов, изменения структуры производства, определения долгосрочных инвестиций, страховок и др. Эти затраты непосредственно не зависят от объема текущего выпуска. Поэтому математические модели долгосрочной задачи фирмы являются задачами безусловной оптимизации. Для моделирования задач фирмы необходимо формализовать такие понятия, как затраты, выпуск, их цены, доход, издержки и производственные возможности фирмы. Не умаляя общности, будем считать, что фирма производит один вид продукта, используя Обозначим через
Поскольку постоянные издержки не связаны с выпуском, то при составлении краткосрочных моделей мы их учитывать не будем. Тогда общий результат производства
Если эта величина положительна, то пара С помощью полученных формул построим математические модели различных задач фирмы. 1. Долгосрочная задача. На долгосрочный период фирма может планировать любые затраты, поэтому модель задачи имеет вид:
Это есть задача безусловной максимизации прибыли. Здесь постоянные затраты
где 2. Краткосрочная задача. Эта задача планируется с учетом наличных на данный период запасов ресурсов, поэтому ее модель строится на условную оптимизацию:
при ограничениях
где
при ограничениях (3.5.2)
Здесь явный вид множества X может быть описан различными способами. Например, в виде
и т.д. 3. Задача многопродуктового производства. Предположим, что фирма выпускает не один, а несколько
и
при ограничениях (3.5.3)
где 4. Задача на минимизацию затрат. Во всех приведенных выше моделях производства ставится задача максимизации прибыли, т.е. целевая функция имеет смысл прибыли. Для постановки задачи на минимизацию затрат предположим, что фирма планирует выпуск продуктов в объемах
при ограничениях (3.5.4)
Желая перевыполнить план выпуска, ограничения-равенства можно заменить на ограничения-неравенства 5. Видоизменения постановок задач. В зависимости от целей и характера исследования производства, можно пользоваться различными модификациями приведенных выше моделей. Например, в задачах (3.5.1) и (3.5.2) по тем или иным техническим соображениям производственную функцию можно исключить из целевой функции, записывая их в виде
при ограничениях
и
при ограничениях
Задачу производства можно поставить в чисто финансовой форме. Предположим, что для приобретения необходимых ресурсов выделена фиксированная сумма
при ограничениях
Любое видоизменение моделей допустимо, если оно адекватно описывает реальную задачу. Оценивается не вид модели, а практическая польза от ее применения. Очевидно, что во всех моделях производства максимизация и минимизация целевой функции осуществляется по переменным Для примера рассмотрим задачу (3.5.3). Если в ней функции
и необходимых условий оптимальности Куна-Таккера (2.3.9)-(2.3.11) Предположим, что все функции в (3.5.3) линейные:
В этом случае целевая функция задачи (3.5.3) принимает вид:
где
Следовательно, приходим к задаче линейного программирования
при ограничениях
где
при ограничениях
имеет смысл минимизации затрат при фиксированном объеме выпуска.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.142 (0.009 с.) |

 видов ресурсов. Эти величины, как и ранее, будем обозначать соответственно через y и
видов ресурсов. Эти величины, как и ранее, будем обозначать соответственно через y и 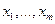 . Предположим, что технология производства достаточно хорошо изучена, т.е. известна производственная функция
. Предположим, что технология производства достаточно хорошо изучена, т.е. известна производственная функция 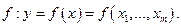
 цену выпускаемой продукции, а через
цену выпускаемой продукции, а через  - цену k -го вида ресурса,
- цену k -го вида ресурса,  . Эти цены порождают понятия дохода (выручки от продажи произведенной продукции) и издержек. Доход от реализации готовой продукции
. Эти цены порождают понятия дохода (выручки от продажи произведенной продукции) и издержек. Доход от реализации готовой продукции 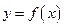 определяется формулой
определяется формулой  . Издержки, соответствующие вектору затрат
. Издержки, соответствующие вектору затрат  , т.е. общие выплаты за все виды затрат, равны
, т.е. общие выплаты за все виды затрат, равны  . Эти издержки называются переменными издержками, так как они связаны (меняются вместе) с объемом выпуска. Кроме того, фирма несет и постоянные издержки (обозначим
. Эти издержки называются переменными издержками, так как они связаны (меняются вместе) с объемом выпуска. Кроме того, фирма несет и постоянные издержки (обозначим  ), связанные с расходами на содержание фирмы. Поэтому общие издержки (обозначим C) складываются из двух компонент:
), связанные с расходами на содержание фирмы. Поэтому общие издержки (обозначим C) складываются из двух компонент: .
. (затраты-выпуск) можно оценить величиной
(затраты-выпуск) можно оценить величиной .
.


 (3.5.1)
(3.5.1) - вектор цен затрат.
- вектор цен затрат.
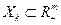 - множество допустимых значений затрат k -го вида. Вводя обозначение
- множество допустимых значений затрат k -го вида. Вводя обозначение  множества допустимых наборов затрат, эту задачу можно написать в векторной форме
множества допустимых наборов затрат, эту задачу можно написать в векторной форме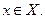
 (параллелепипеда)
(параллелепипеда) (многогранника)
(многогранника) (криволинейного многообразия)
(криволинейного многообразия) видов продуктов. Пусть для каждого
видов продуктов. Пусть для каждого 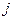 -го вида продукта известны производственная функция
-го вида продукта известны производственная функция  и цена
и цена 
 ; для каждого k -го вида ресурса известны функция
; для каждого k -го вида ресурса известны функция  , описывающая суммарные затраты этого ресурса для производства всех
, описывающая суммарные затраты этого ресурса для производства всех 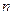 видов продуктов, и его наличное количество
видов продуктов, и его наличное количество 



 - вектор цен выпускаемых товаров,
- вектор цен выпускаемых товаров,  - вектор-функция затрат,
- вектор-функция затрат,  - вектор наличных запасов ресурсов.
- вектор наличных запасов ресурсов. , т.е. рассмотрим фиксированные объемы выпуска. В этом случае оптимизационная задача производства может быть поставлена следующим образом:
, т.е. рассмотрим фиксированные объемы выпуска. В этом случае оптимизационная задача производства может быть поставлена следующим образом:






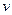 . Тогда задачу максимизации дохода можно поставить в следующей форме:
. Тогда задачу максимизации дохода можно поставить в следующей форме:

 векторов затрат. Выбор метода нахождения оптимального решения задач зависит прежде всего от линейности или нелинейности участвующих в их постановке функций
векторов затрат. Выбор метода нахождения оптимального решения задач зависит прежде всего от линейности или нелинейности участвующих в их постановке функций  и
и  . Если эти функции нелинейны, то соответствующую задачу можно решить методом множителей Лагранжа или каким-либо приближенным методом. В случае линейности всех функций можно применить симплекс-метод.
. Если эти функции нелинейны, то соответствующую задачу можно решить методом множителей Лагранжа или каким-либо приближенным методом. В случае линейности всех функций можно применить симплекс-метод.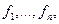
 дифференцируемы в
дифференцируемы в  и среди них имеются нелинейные, то ее оптимальное решение
и среди них имеются нелинейные, то ее оптимальное решение 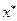 можно найти с помощью функции Лагранжа
можно найти с помощью функции Лагранжа

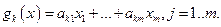

 с ограничениями:
с ограничениями:


 A - технологическая матрица, элементы
A - технологическая матрица, элементы  которой показывают расход ресурса вида i для производства единицы продукта вида k. Двойственная к ней задача:
которой показывают расход ресурса вида i для производства единицы продукта вида k. Двойственная к ней задача:




