
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи фирмы. Геометрическая иллюстрацияСодержание книги
Поиск на нашем сайте
Пусть в задаче (3.5.1) производственная функция f дважды дифференцируема в
где
В силу предположения о выполнении (3.2.3) эти условия становятся и достаточными условиями оптимальности. Упростим их, предположив С учетом последнего предположения из условия дополняющей нежесткости следует
Величину
Обозначим
и составим матрицу Якоби для системы (3.6.1):
Из алгебры известно, что если матрица Якоби невырожденна, то система (3.6.1) имеет решение. Здесь невырожденность следует из условий (3.2.2)-(3.2.3). Таким образом, система (3.6.1) разрешима и оптимальное решение задачи (3.5.1) может быть выражено как функция
В координатной форме имеем
выражающих оптимальные объемы затрат в зависимости от цен. Интересно заметить, что спрос не зависит от масштаба цен, точнее, от пропорционального изменения цены продукции и цен ресурсов. Действительно, из (3.5.1) для любых
Так как постоянный коэффициент
имеет такое же оптимальное решение, что и задача (3.5.1). Следовательно,
и функции спроса на затраты являются однородными нулевой степени функциями. Подставляя решение (3.6.2) в производственную функцию f, получаем выпуск как функцию от тех же
Это есть функция предложения готовой продукции. Так как
то функция предложения также является однородной нулевой степени функцией, т.е. объем предложения товара остается неизменным при повышении (снижении) цен на ресурсы, если в той же пропорции повышается (снижается) цена готовой продукции.
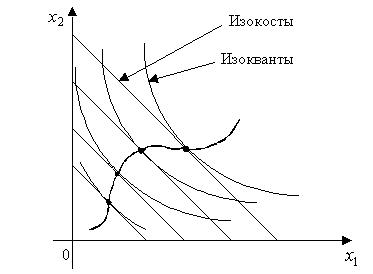
Рассмотрим геометрическую иллюстрацию оптимального решения (3.6.2) задачи (3.5.1) в пространстве затрат. Для этого введем два геометрических понятия - изокванты и изокосты.
Рис. 3.3 Изокванта
Определение 3.2. Изоквантой (производственной функции Таким образом, изокванта - это линия уровня производственной функции. Для различных уровней выпуска
Рис. 3.4 Особая область
Пусть производственная функция
Отсюда находим отношение:
Следовательно, наклон Аналогично проведем касательные к изоквантам с наклоном Построенная область в Граница первого ресурса Г-1 является геометрическим местом минимального количества затрат
Определение 3.3. Изокостой называется геометрическое место векторов затрат, для которых издержки производства постоянны:
Рис. 3.5 Изокосты
Для двухфакторного производства изокоста задается уравнением
Так как цены
Следовательно, для разных констант изокосты являются параллельными линиями с одним и тем же наклоном Сравнивая (3.6.4) и (3.6.5), получаем
Покажем, что равенство (3.6.6) достигается именно в точке
Деля первое равенство на второе почленно, получаем
Рис. 3.6 Долгосрочный путь расширения
Рис. 3.7 Краткосрочный путь
Сопоставляя полученное равенство с (3.6.4) и (3.6.5), приходим к выводу: совпадение наклонов изокванты и изокосты имеет место в одной и той же точке Так как изокванты и изокосты заполняют все пространство затрат, соединяя все точки их касания, получаем непрерывную линию. Очевидно, эта линия расположена в особой области, изображенной на рисунке 3.4, и потому чем дальше на ней расположена точка В случае краткосрочной задачи (3.5.2) (или (3.5.3)) необходимый и достаточный признак оптимальности будет иметь более сложный, чем (3.6.1), вид из-за наличия ограничений. Однако и в этом случае при выполнении условий (3.2.2)-(3.2.3) краткосрочный путь расширения, как геометрическое место векторов оптимальных затрат, будет проходить в особой области. Причем можно высказать гипотезу о том, что если множество допустимых затрат X (см. задачу (3.5.2)) краткосрочной задачи имеет непустое пересечение с долгосрочным путем расширения, то краткосрочный путь расширения совпадает (в области X) с долгосрочным путем, т.е. он является частью долгосрочного пути расширения (в случае Если эта гипотеза верна, то для каждой точки
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.187.121 (0.009 с.) |

 и удовлетворяет условиям (3.2.2)-(3.2.3). Для нахождения ее оптимального решения
и удовлетворяет условиям (3.2.2)-(3.2.3). Для нахождения ее оптимального решения  (относительно затрат) построим функцию Лагранжа
(относительно затрат) построим функцию Лагранжа
 и выпишем необходимые условия Куна-Таккера:
и выпишем необходимые условия Куна-Таккера: (стационарность)
(стационарность) (дополняющая нежёсткость)
(дополняющая нежёсткость) (допустимость)
(допустимость) . Содержательно это означает необходимость затрат всех видов. Это условие не является жестким, так как в случае
. Содержательно это означает необходимость затрат всех видов. Это условие не является жестким, так как в случае  можно было исключить ресурс k -го вида из рассмотрения, сократив тем самым размерность пространства затрат.
можно было исключить ресурс k -го вида из рассмотрения, сократив тем самым размерность пространства затрат.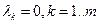 . Заметим сразу, что это не противоречит условию о невозможности одновременного равенства нулю всех множителей Лагранжа - оно является следствием изменения условия задачи (3.5.1). В результате необходимый и достаточный признак оптимальности принимает вид:
. Заметим сразу, что это не противоречит условию о невозможности одновременного равенства нулю всех множителей Лагранжа - оно является следствием изменения условия задачи (3.5.1). В результате необходимый и достаточный признак оптимальности принимает вид: (3.6.1)
(3.6.1) называют стоимостью предельного продукта. Поэтому (3.6.1) содержательно означает равенство стоимости предельного продукта и платы за ресурсы в точке
называют стоимостью предельного продукта. Поэтому (3.6.1) содержательно означает равенство стоимости предельного продукта и платы за ресурсы в точке  :
:
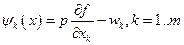
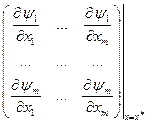
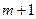 параметров:
параметров:  :
: . (3.6.2)
. (3.6.2) функций спроса на затраты
функций спроса на затраты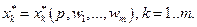
 имеем:
имеем: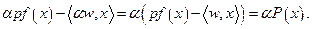
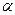 не влияет на максимизацию функции P по x, то задача
не влияет на максимизацию функции P по x, то задача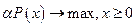

 . (3.6.3)
. (3.6.3)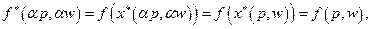

 называется геометрическое место всех векторов затрат
называется геометрическое место всех векторов затрат  , использование которых приводит к одному и тому же объему выпуска продукции
, использование которых приводит к одному и тому же объему выпуска продукции 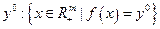 .
. линии уровня
линии уровня 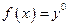 заполняют все пространство затрат
заполняют все пространство затрат  и составляют карту изоквант. Для примера на Рис.3.3 приведен вид изоквант
и составляют карту изоквант. Для примера на Рис.3.3 приведен вид изоквант 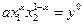
 производственной функции Кобба-Дугласа.
производственной функции Кобба-Дугласа.
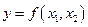 дифференцируема по обеим переменным. Тогда вдоль изокванты
дифференцируема по обеим переменным. Тогда вдоль изокванты 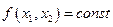 имеем:
имеем: .
. (3.6.4)
(3.6.4) изокванты производственной функции выражается через отношение предельных продуктов. Дальнейшие геометрические построения, связанные с изоквантами, проведем на (Рис.3.4). Имея карту изоквант
изокванты производственной функции выражается через отношение предельных продуктов. Дальнейшие геометрические построения, связанные с изоквантами, проведем на (Рис.3.4). Имея карту изоквант 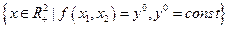 , проведем касательные к каждой из них с наклоном
, проведем касательные к каждой из них с наклоном 
 Эти касательные проходят параллельно к оси
Эти касательные проходят параллельно к оси  . Так как изокванты заполняют все пространство
. Так как изокванты заполняют все пространство 
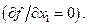 Эти касательные проходят параллельно к оси
Эти касательные проходят параллельно к оси 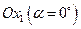 . Соединяя точки касания, получаем непрерывную линию Г-2, которую назовем границей второго ресурса.
. Соединяя точки касания, получаем непрерывную линию Г-2, которую назовем границей второго ресурса. , так как для
, так как для 
 неположителен. Можно показать, что в особой области справедливы и неравенства (3.2.3), т.е. это та область затрат, где выполнен закон убывающей доходности. Пользуясь условиями (3.2.3), можно доказать, что особая область является выпуклым подмножеством пространства затрат.
неположителен. Можно показать, что в особой области справедливы и неравенства (3.2.3), т.е. это та область затрат, где выполнен закон убывающей доходности. Пользуясь условиями (3.2.3), можно доказать, что особая область является выпуклым подмножеством пространства затрат.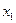 , необходимых для производства различных уровней выпуска. Например, для производства продукции в размере
, необходимых для производства различных уровней выпуска. Например, для производства продукции в размере  единиц (Рис. 3.4). Точно также, граница второго ресурса Г-2 является геометрическим местом минимального количества затрат
единиц (Рис. 3.4). Точно также, граница второго ресурса Г-2 является геометрическим местом минимального количества затрат 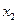 , необходимых для производства различных уровней выпуска. Например, чтобы произвести продукцию в количестве
, необходимых для производства различных уровней выпуска. Например, чтобы произвести продукцию в количестве  , необходимо как минимум
, необходимо как минимум  единиц второго ресурса.
единиц второго ресурса.

 .
.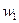 и
и  предполагаются заданными, дифференцируя последнее уравнение, находим:
предполагаются заданными, дифференцируя последнее уравнение, находим: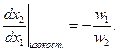 (3.6.5)
(3.6.5)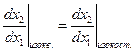 (3.6.6)
(3.6.6)



 см. Рис. 3.7).
см. Рис. 3.7). на краткосрочном пути существует такое постоянное число
на краткосрочном пути существует такое постоянное число  , что изокоста
, что изокоста 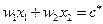 и изокванта
и изокванта  из долгосрочной задачи будут иметь точкой касания точку
из долгосрочной задачи будут иметь точкой касания точку 


