
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ влияния цен на объемы затрат и выпуска. Основное уравнение фирмыСодержание книги
Поиск на нашем сайте
Исследуем чувствительность оптимальных затрат и выпуска к изменениям параметров Подставляя в систему (3.6.1) функции спроса (3.6.2) и присоединяя к ней выражение для функции предложения (3.6.3), получим замкнутую тождественную систему из
Так как чувствительность оптимальных затрат и выпуска по ценам оценивается величинами
то систему (3.7.1) будем дифференцировать по переменным
Будем считать выполненными условия (3.2.2)-(3.2.3), т.е. анализ чувствительности затрат и выпуска проведем в пределах особой области, изображенной на рисунке 3.4. Продифференцируем сначала обе части системы (3.7.1) по
Применяя обозначение матрицы Гессе
перепишем эту систему в векторной форме:
Продифференцируем теперь систему (3.7.1) по
где
перепишем эту систему в векторной форме:
Запишем системы (3.7.2) и (3.7.3) в матричных формах:
где через Объединяя уравнения (3.7.4) и (3.7.5) в одно, получим основное матричное уравнение теории производства (фирмы):
Это есть система из
Выполняя матричное умножение в последнем уравнении, находим решение. Запишем его в векторной форме:
где Так же как и в теории потребления, при помощи показателей сравнительной статики можно классифицировать типы затрат. Определение 3.4. Затраты (ресурсы) вида k называются нормальными, если Неравенство
Некоторые выводы относительно чувствительности затрат и выпуска по ценам, к которым можно прийти, анализируя соотношения (3.7.7)-(3.7.10), следующие: 1. повышение цены на выпускаемый продукт всегда приводит к увеличению объема выпуска; 2. повышение цены на выпускаемый продукт влечет повышение спроса на некоторые виды затрат; 3. в рамках закона об убывающей доходности нельзя обходиться исключительно малоценными затратами; 4. повышение платы за малоценные ресурсы ведет к увеличению объема выпуска; 5. повышение платы за некоторый вид затрат приводит к увеличению объема выпуска; 6. повышение цен на затраты приводит к сокращению спроса на них; 7. чувствительность объема затрат k -го вида на изменение цен затрат i -го вида такая же, что и чувствительность объема затрат i -го вида на изменение цен затрат k -го вида; 8. для взаимозаменяемых затрат повышение (понижение) цены одной из них влечет увеличение (уменьшение) спроса на другую; 9. для взаимодополняющих друг друга затрат повышение (понижение) цены одной из них влечет уменьшение (увеличение) спроса на другую. Проведём краткое обоснование этих утверждений. Первый вывод следует из неравенства
которое вытекает из (3.7.7) с учетом отрицательной определенности обратной матрицы Гессе Неравенство (3.7.11) с учетом (3.7.1) запишется в виде
Такое соотношение возможно только в том случае, если для некоторых k будет выполнятся неравенство
которое и является обоснованием второго вывода. Сравнивая (3.7.8) и (3.7.9), можно заметить, что
Поэтому вывод 2. можно уточнить следующим образом: повышение цены выпускаемой продукции приводит к повышению спроса на затраты k -го вида всегда, если и только если увеличение платы за этот вид затрат приводит к сокращению объема выпуска. Действительно, с учетом (3.7.14) неравенство (3.7.13) влечет неравенство
Обоснованность вывода 3. следует также из неравенства (3.7.14). Из соотношений (3.7.11), (3.7.12) и (3.7.14) получаем:
Поэтому в особой области для некоторых видов затрат выполнено неравенство
Оно доказывает справедливость вывода 5. Соотношение (3.7.10) указывает на симметричность матрицы
Отсюда следует вывод 6. Симметричность матрицы
Содержательный смысл этого равенства приведен в выводе 7. Выводы 8. и 9. вытекают непосредственно из определений взаимозаменяемых и взаимодополняемых затрат.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.247.95 (0.006 с.) |

 . Для этого сделаем дополнительное к условиям предыдущего параграфа предположение: функции
. Для этого сделаем дополнительное к условиям предыдущего параграфа предположение: функции  и
и  дифференцируемы по всем переменным.
дифференцируемы по всем переменным.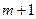 уравнения на
уравнения на  (3.7.1)
(3.7.1)
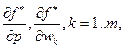
 частных производных характеризуют изменение оптимального объема затрат при изменении цены готовой продукции и цен ресурсов; вторая группа частных производных показывает реакцию объема оптимального выпуска на колебание тех же цен. Обозначим:
частных производных характеризуют изменение оптимального объема затрат при изменении цены готовой продукции и цен ресурсов; вторая группа частных производных показывает реакцию объема оптимального выпуска на колебание тех же цен. Обозначим:


 :
:
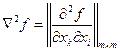
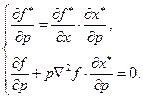 (3.7.2)
(3.7.2) :
:
 - символ Кронекера. Используя обозначение единичной матрицы
- символ Кронекера. Используя обозначение единичной матрицы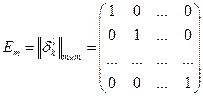
 (3.7.3)
(3.7.3) (3.7.4)
(3.7.4) (3.7.5)
(3.7.5) обозначен m -мерный вектор-столбец с нулевыми элементами,
обозначен m -мерный вектор-столбец с нулевыми элементами,  - знак транспонирования.
- знак транспонирования.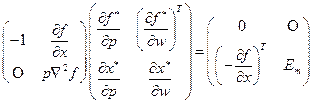 . (3.7.6)
. (3.7.6) уравнений с
уравнений с 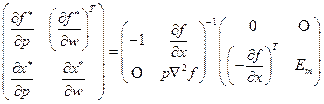 .
. (3.7.7)
(3.7.7) (3.7.8)
(3.7.8)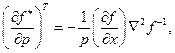 (3.7.9)
(3.7.9) (3.7.10)
(3.7.10)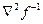 - обратная матрица Гессе.
- обратная матрица Гессе. ; ценными (малоценными), если
; ценными (малоценными), если 
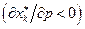 . Два вида затрат i и k называются взаимозаменяемыми (взаимодополняемыми), если
. Два вида затрат i и k называются взаимозаменяемыми (взаимодополняемыми), если 


 означает возрастание затрат k -го вида с ростом их цены. Такие затраты исключены, так как напрямую уменьшают прибыль фирмы (см. целевые функции задач (3.5.1) - (3.5.3)). Поэтому кривая спроса на затраты всегда является убывающей и, в отличие от теории потребления, здесь нет товаров Гиффина.
означает возрастание затрат k -го вида с ростом их цены. Такие затраты исключены, так как напрямую уменьшают прибыль фирмы (см. целевые функции задач (3.5.1) - (3.5.3)). Поэтому кривая спроса на затраты всегда является убывающей и, в отличие от теории потребления, здесь нет товаров Гиффина. , (3.7.11)
, (3.7.11) и неотрицательности предельного продукта
и неотрицательности предельного продукта  в особой области. Данное неравенство подтверждает факт о том, что кривая предложения продукта является возрастающей.
в особой области. Данное неравенство подтверждает факт о том, что кривая предложения продукта является возрастающей. (3.7.12)
(3.7.12) (3.7.13)
(3.7.13) (3.7.14)
(3.7.14) . В частности, если
. В частности, если  - малоценные затраты (т.е.
- малоценные затраты (т.е.  ), то увеличение цены
), то увеличение цены  ), о чем и утверждает вывод 4.
), о чем и утверждает вывод 4.

 , причем, как и правая часть этого уравнения, она отрицательно определена. Поэтому ее диагональные элементы отрицательны:
, причем, как и правая часть этого уравнения, она отрицательно определена. Поэтому ее диагональные элементы отрицательны:




