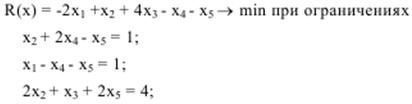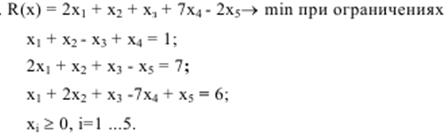Решение задач оптимизации данных

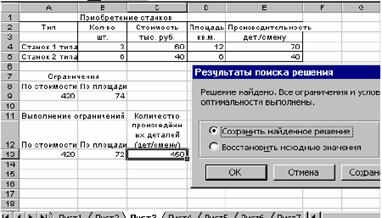
Microsoft Excel предлагает мощный инструмент  для решения оптимизационных задач, то есть таких задач, в которых необходимо найти экстремальное значение (минимум или максимум) некоторой функции, называемой целевой, при заданных ограничениях.

Если целевая функция и/или ограничения линейны, то такие задачи принято называть задачами линейного программирования. Многие задачи решаются в рамках линейного программирования. Целевой функцией в них является либо прибыль или объем производства, которые надо максимизировать, либо затраты (издержки), которые надо минимизировать. Ограничения  – обычно это условия, которые накладываются на используемые ресурсы для производства продукции.

Построив математическую модель и решив задачу при заданных ограничениях, можно варьировать ограничениями. В этом случае речь уже идет о математическом моделировании с помощью Excel.

Пример задачи:

В цехе площадью 74 м² необходимо установить станки; на приобретение которых отпущено 420 тыс. руб.

Существует два типа станков. Станок  первого типа стоимостью 60 тыс. руб., требующий 12м² производственных площадей, обеспечивает изготовление 70 изделий в смену. Аналогичные характеристики станка второго типа составляют соответственно 40 тыс.  руб., 6 м2, 40 изделий в смену.

Найти оптимальный вариант приобретения станков, обеспечивающий максимальное производство изделий в цехе.

Решение:

Обозначим Х1 количество станков первого типа, а Х2 – количество станков второго типа, которые предполагается установить в цехе. Тогда количество изделий, которое будет произведено на этих станках равно:

F(X1, X2) =70 * X1 +40 * X2

Это и есть целевая функция, которую нужно максимизировать.

Теперь запишем ограничения. Их в задаче два.

Ограничения по финансам:

60 *Х1 +40 *Х2 £ 420 тыс. руб.

Ограничения по площади размещения:

12* Х1 +6* Х2 £ 74м²

Кроме этих ограничений следует добавить очевидные ограничения:

– переменные задачи должны быть неотрицательными: 

Х1 ³ 0; Х2 ³ 0;

– переменные задачи должны быть целочисленными:

X1, X2 Î Z.

Итак, математическая модель построена.

Решение оптимизационных задач в  Excel проводится с помощью специализированной программы Поиск решения, вызываемой из вкладки

Данные/Поиск решения. Она находится в файле SOLVER.XLA, который подключается при первом обращении к этой программе. 

Таким образом, теперь задача состоит в том, чтобы перенести математическую модель в Excel. Порядок действий следующий.

1. Отводим ячейки для каждой независимой переменной задачи. В нашем

примере это ячейка В4 для X1, и ячейка В5 для X2; (рис. 1). Их можно оставить

пустыми.

2. Отводим ячейку (С13) для целевой функции и набираем в ней

соответствующую формулу:

= В4*Е4+В5*Е5.

В формуле в качестве переменных фигурируют адреса ячеек, где расположены соответствующие переменные. Константы задачи заданы не числами, а также ссылками на ячейки, в которых их необходимо предварительно разместить. Рекомендуется для этого оформить таблицу, например, так, как это показано на рис. 1.

Рис.1. Рабочий лист с результатом решения задачи оптимизации

3. Отводим ячейки (А13 и В13) для создания формул, соответствующих

левой части каждого ограничения:

=В4*С4+В5*С5

=B4*D4+B5*D5 4.

Открываем диалоговое окно Поиск решения (рис. 2).

Рис. 2. Диалоговое окно Поиск решения с заданными значениями 

и адресами ячеек.

5. В поле Установить целевую ячейку указываем адрес ячейки, в которой находится формула для расчета целевой  функции (ячейка С13). Ниже указываем тип оптимизации (поиск максимума или минимума).

6. В поле Изменяя ячейки отмечаем адреса ячеек, где находятся независимые переменные задачи (В4 и В5).

7. Для того чтобы ввести ограничения, нужно нажать на кнопку Добавить.

Появляется диалоговое окно Добавление ограничения (рис.3).

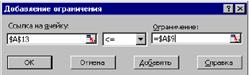
Рис. 3. -Диалоговое окно Добавление ограничения

В левое поле вводим адрес ячейки, где находятся ограничения (или диапазон адресов ячеек), в центральном поле выбираем знак операции отношения (а также задаем целочисленность или бинарность переменных), в правом поле задаем адрес ячейки (или диапазон адресов), где находятся правые части ограничений. Вместо адресов в правой части можно просто задать числовые значения.

Нажатием клавиши Добавить переходим в режим добавления следующего ограничения, нажатием клавиши ОК заканчиваем ввод ограничений. Теперь, если необходимо, в поле Ограничения окна Поиск решения можно выбирать какие-либо ограничения и редактировать их или удалять.

8. Запускаем процесс вычислений нажатием кнопки Выполнить. Результат приведен на рис.1. Заданным ограничениям удовлетворяет следующий парк станков: 3 – первого типа, 6 – второго типа; при этом будет изготовлено максимальное количество деталей – 450.

В окне Поиск решения с помощью кнопки Параметры можно вызвать

диалоговое окно Параметры поиска решения (рис.4).

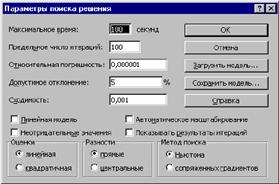
Рис.4. Диалоговое окно Параметры поиска решения

Рассмотрим элементы этого окна. 

Поля Максимальное время и Предельное число итераций определяют время, отпущенное на поиск решения задачи, и число Промежуточных вычислений, соответственно.

Поля Относительная погрешность, Допустимое отклонение и Сходимость служат для задания точности, с которой ищется решение (последнее используется только для нелинейных моделей). Рекомендуется после решения задачи повторить его с большей точностью (особенно для целочисленных моделей), чтобы проверить точность модели.

Флажок Линейная модель устанавливается для линейных задач и снимается для нелинейных.

Флажок Неотрицательные значения позволяет установить Нулевую нижнюю границу для тех ячеек, для которых она не была Указана в поле Ограничение диалогового окна Добавить ограничение.

Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по

отношению к вложениям, исчисляемым в миллионах рублей.

Флажок Показывать результаты итераций служит для пошагового проведения итераций с целью просмотра промежуточных результатов.

Опция Оценки служит для указания метода экстраполяции, используемого при поиске решения.

Опция Разности служит для указания метода численного дифференцирования, который используется для вычисления производных при поиске решения.

Опция Метод поиска служит для выбора алгоритма оптимизации (метод Ньютона или сопряженных градиентов) для указания направления поиска.

Более подробную информацию можно получить, нажав кнопку Справка в том же диалоговом окне.

Практическое задание 1:  Пусть уже построена математическая модель некоторой оптимизационной задачи. Найти оптимальное значение целевой функции R(x) при заданных ограничениях с помощью сервисной программы Excel Поиск решения.

2.

3.

 

Вопросы и задания для контроля знаний.

1. Что такое оптимизация функции? 2. Что называют целевой функцией? 3.Что является ограничением в задаче оптимизации? 4.Какой инструмент Excel применяют для решения задачи оптимизации? 5. Какие параметры нужно ввести в окне Поиск решения? 6. Какие параметры поиска решения можно настроить?

Тема 25 «Работа с MS Excel. Решение задач оптимизации данных»

Цель – формирование практических умений и навыков решения задач оптимизации данных.

План