
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация технологических процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Оптимизация технологических процессов
Учебное пособие для обучающихся по направлениям «Продукты питания животного происхождения», «Технология производства и организация общественного питания», «Биотехнология»
Мурманск, 2020
УДК 65.012.2:338.439.4
Рецензенты: О. Н. Красуля, д-р техн.наук, профессор ФГБОУ ВО «РГАУ-МСХА им. Тимирязева К. А.»; А.В. Барышников, канд. техн. наук, научный сотрудник лаборатории технологии переработки водных биоресурсов Полярного филиала ФГБНУ «ВНИРО»; Л.А. Шаповалова, канд. техн. наук, и.о. зав. лабораторией технологии переработки водных биоресурсов Полярного филиала ФГБНУ «ВНИРО».
Авторы: Василий Игоревич Волченко, канд. техн. наук, доцент кафедры технологий пищевых производств Мурманского государственного технического университета; Инна Эдуардовна Бражная, канд. техн. наук, профессор кафедры технологий пищевых производств Мурманского государственного технического университета
Аннотация: учебное пособие предназначено для обучающихся по направлениям 19.03.01«Биотехнология», 19.03.03 «Продукты питания животного происхождения», 19.04.04 «Технология производства и организация общественного питания» и изучающим дисциплины, связанные с оптимизацией технологических процессов в пищевой промышленности и в общественном питании. В пособии приводится краткая характеристика задач оптимизации, рассматриваются основные этапы оптимизации, а также практические работы по дисциплине.
Оглавление Введение: понятие об оптимизации. Основные этапы оптимизации. 4 1. Критерий оптимальности. Обобщённый параметр оптимизации. 5 Практическая работа № 1. Метод экспертных оценок (априорное ранжирование параметров) 9 2. Факторы, виды, выбор. 12 Практическая работа № 2. Нормирование факторов и параметров оптимизации. 13 3. Дисперсионный анализ. 15 Практическая работа № 3. Однофакторный дисперсионный анализ. 16 4. Обработка экспериментальных данных. 19 5. Теория планирования эксперимента. 22 Практическая работа № 4. Планирование двухфакторного эксперимента и обработка данных 26 Практическая работа № 5. Поиск значимых факторов с помощью плана Плакетта-Бермана. 28 Практическая работа № 6. Оптимизация методом «крутое восхождение». 30 6. Методы безусловной оптимизации. 33 Практическая работа № 7 Использование СПО «Maxima» с целью оптимизации. 34 Практическая работа № 8. Расчет предельных значений функций, изменяющихся по экспоненте 40 7. Понятие об условной оптимизации. 42 Практическая работа № 9. Оптимизация методом неопределенных множителей Лагранжа. 43 7. Классификация и кластеризация. 45 Практическая работа № 10. Изучение методов кластерного анализа. 46 8. Искусственные нейронные сети. 47 Практическая работа № 11. Использование ИНС в задачах классификации. 50 Практическая работа № 12. Использование искусственных нейронных сетей для решения задач интерполяции. 51 Список использованной литературы.. 53
Практическая работа № 1 Метод экспертных оценок (априорное ранжирование параметров)
Цель работы: определить коэффициенты значимости параметров оптимизации Задачи: 1. Выбрать параметры оптимизации по заданию 2. Составить таблицу для проведения экспертной оценки 3. Провести опрос экспертов 4. Провести обработку результатов опроса методом ранжирования 5. Рассчитать коэффициент конкордации 6. Выбирают коэффициенты значимости на основе суммы рангов. Ход работы Выявленные в прошлой работе параметры оптимизации (управляемые параметры) дают на оценку значимости группе экспертов. Оценку проводят в форме таблицы. Для более точной оценки экспертам предлагают оценить значимость параметра по шкале от 0 до 10, причём 0 ставится в исключительных случаях при полном отсутствии влияния параметра на общую оценку.
Таблица 1.1 – Лист для экспертной оценки значимости параметров
Далее проводят ранжирование на основе таблицы 1, заполняя таблицу 1.2
Таблица 1.2 – Ранговая оценка экспертов
Заполнение таблицы 2 осуществляют последовательно по столбцам, выбирая в каждом максимальную оценку и выставляя ей первый ранг, следующей оценке ставят второй и т.п. При наличии одинаковых оценок у одного эксперта для двух разных факторов выставляют «дробный ранг» (иногда выставляют числовое значение ранга, но оно не точно отражает результат в дальнейшей обработке) для обоих факторов. Для трёх и более одинаковых оценок также ставят усреднённый ранг. Например, если по четырём факторам был получен наивысший балл, всем им присваивают ранг (1+2+3+4)/4=2,5. После этого рассчитывают сумму рангов по каждому показателю для всех экспертов si. Далее рассчитывают среднее значение между всеми si, а потом – сумму квадратов отклонений рангов S. После этого проводят расчёт коэффициента конкордацииW и оценивают его значимость по критерию Фишера или Пирсона. В случае недостаточной согласованности экспертную оценку повторяют. Коэффициенты значимости рассчитывают по средней оценке значимости, полученной в таблице 1. При необходимости её нормируют – делят на максимально возможную (10) и на число параметров m. В этом случае сумма всех коэффициентов значимости будет равна 1. В случае степенного подхода нормирование осуществляют иначе: среднее значение делят на 5. В этом случае коэффициент значимости будет меняться от 0 (для абсолютно незначимых параметров, в итоге они не будут влиять на результат) до 2 (для очень значимых параметров, они будут влиять на общую оценку квадратично). Если интервал коэффициентов значимости надо расширить, результаты возводят в степень, большую 1, если сузить – то в степень от 0 до 1 (не включая границы). Содержание отчёта Отчёт представляют, как правило, в электронном виде (в системе ЭИОС) в виде файла (файлов) в формате Wordили Excel; допускается использование отдельных файлов-фотографий листов в форматах pngили jpeg. В последнем случае файлы должны быть пронумерованы в соответствии с номером страницы в отчёте. При временной неработоспособности системы ЭИОС или отсутствии необходимости в ней (например, при индивидуальном обучении) отчёт по работе представляют в печатном виде. Отчёт должен содержать следующие обязательные и факультативные разделы: - название работы (обязательно) - цель и задачи работы (факультативно) - краткие теоретические сведения (факультативно) - ход работы (обязательно), включая таблицы 1.1, 1.2 и необходимые расчёты (можно оформить в виде таблицы в MSExcelили LibreOfficeCalc). - вывод о согласованности (несогласованности) мнений экспертов. Вопросы для самоконтроля 1. Что такое обобщённый параметр оптимизации? 2. Что такое коэффициент значимости? 3. Как можно определить коэффициенты значимости частных параметров оптимизации? 4. Что такое согласованность и несогласованность мнений экспертов? Практическая работа № 2 Ход работы Обучающиеся получают задание, включающее наименование оптимизируемого процесса, предлагаемые факторы и параметры оптимизации (с направлением оптимизации) и их естественные границы. Задача обучающихся – провести нормализацию факторов и параметров оптимизации, т.е. написать формулу, переводящую любое значение каждого фактора (параметра) в нормализованное значение, а также рассчитать пограничные значения. Для факторов следует предположить, что они будут использованы в ЦКРП, т.е. рассчитать значения исходных факторов, соответствующие нормализованным–1; 0; +1; Содержание отчёта Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить расчёт уровней варьирования факторов. В качестве вывода следует привести числовые значения уровней варьирования факторов, а также расчётную формулу для получения нормированных значений каждого из параметров оптимизации. Вопросы для самоконтроля 1. Что такое факторы? 2. В чём заключается процедура нормирования (масштабирования) факторов? 3. Чем определяется выбор диапазона варьирования того или иного фактора? Задания для работы [2]. 1. Процесс обезвоживания. Факторы: температура от 25 до 95 °С, время от 0 до 120 минут. Параметры оптимизации: степень обезвоживания эмульсии от 0 до 100 % (максимизировать), энергозатраты от 0 до 40000 кДж (минимизировать). 2. Созревание слабосолёной сельди. Факторы: солёность от 2 до 10 %, продолжительность созревания от 0 до 30 суток, степень удаления внутренностей, от 0 до 100 %. Параметры оптимизации: уровень качества от 0 до 100 % (максимизировать), буферность, от 20 до 300 градусов (оптимум – 150 градусов). 3. Сухой посол рыбы. Факторы: температура от минус 4 до 25 °С, дозировка соли от 4 до 20 % к массе солёной рыбы, жирность рыбы от 1 до 20 %. Параметры оптимизации: выход солёной рыбы от 60 до 170 % (максимизировать), уровень качества от 0 до 100 % (максимизировать). 4. Морозильное хранение жирных продуктов (в течение 2 месяцев). Факторы: температура от минус 33 до минус 6 °С, масса нетто упаковки от 0,3 до 20 кг. Параметры оптимизации: кислотное число липидов от 0 до 60 мг КОН/г (минимизировать), альдегидное число липидов от 0 до 100 мг % (минимизировать), lgКМАФАнМ от 0 до 8 (минимизировать) 5. Подбор рецептуры паштетных консервов. Факторы: доля яичного порошка от 5 до 20 %, дозировка соуса на банку № 3 от 30 до 110 г. Параметры оптимизации: доля отслаивающегося жира от 0 до 25 % (минимизировать), уровень качества от 0 до 100 % (максимизировать), массовая доля жира от 20 до 70 % (максимизировать). 6. Подбор рецептуры мясорыбных колбас с печенью трески. Факторы: соотношение печени к мясу от 0 до 1,5; дозировка крахмала от 0 до 20 % к массе мясорыбного сырья; дозировка яичного порошка от 0 до 10 % к массе мясорыбного сырья. Параметры оптимизации: уровень качества от 0 до 100 % (максимизировать), усилие резания от 0 до 2000 гс (оптимум 150 гс). 7. Подбор рецептуры хлеба с добавками отрубей и ламинарии. Факторы: дозировка сушёной ламинарии (% от массы муки) от 0 до 6; дозировка отрубей (% от массы муки) от 0 до 50. Параметры оптимизации: уровень качества от 0 до 100 %, пористость от 0 до 95 % (оптимум 85 %), кислотность от 0 до 2,5 % (оптимум 1,5 %). 8. Подбор рецептуры котлет. Факторы: дозировка хлеба в котлетной массе от 0 до 60 %; дозировка панировки от 0 до 15 % к массе изделия; количество добавляемой воды в рецептуру от 0 до 30 %. Параметры оптимизации: уровень качества от 0 до 100 % (максимизировать), усилие резания (от 0 до 2000 гс, оптимум 200 гс). 9. Вяление рыбы. Факторы: средняя температура воздуха (от 10 до 30 °С), средняя влажность воздуха (от 30 до 80 %), продолжительность периодов «отдыха» (каждые 8 ч) – от 0 до 3 ч. Параметры оптимизации: продолжительность от 1 до 10 суток (минимизировать), уровень качества от 0 до 100 %; влажность от 0 до 50 %, выше – ограничение (оптимум 45 %). 10. Варка мяса. Факторы: температура бульона от 80 до 103 °С; продолжительность от 10 до 70 минут; толщина кусков от 5 до 100 мм. Параметры оптимизации: температура в центре от 75 до 100 °С (максимизировать), уровень качества от 0 до 100 % (максимизировать), выход от 60 до 110 % (максимизировать).
Дисперсионный анализ
Одним из способов, позволяющих сузить факторное пространство, отбросив факторы, незначимо и малозначимо влияющие на параметр(ы) оптимизации, является дисперсионный анализ. Дисперсионный анализ – статистический метод, основанный на оценке зависимости экспериментальных данных путём сравнения средних значений. Дисперсионный анализ может быть одно- и многофакторным. Однофакторный дисперсионный анализ позволяет выявить наличие или отсутствие влияния одного фактора на параметр оптимизации, причём на этом этапе фактор не обязательно должен принимать числовые значения. В качестве фактора могут быть выбраны величины, не выражающиеся явным образом в числовом виде, например, форма объекта, способ охлаждения или нагревания, вид упаковки и т.д. В однофакторном дисперсионном анализе необходимо провести несколько повторных опытов (определяя в каждом параметр оптимизации) для каждого из нескольких значений рассматриваемого фактора (как минимум, двух, но для обеспечения достаточной значимости результата лучше 3-5). Для каждой выборки (серии повторных опытов) определяют математическое ожидание, приблизительно оцениваемое по среднему арифметическому результатов (значений параметра оптимизации). Далее считают сумму квадратов отклонений по каждому опыту от математического ожидания в данной выборке. Сумму квадратов отклонений делят на число степеней свободы (общее число опытов за вычетом единицы), получая при этом внутригрупповую дисперсию. Межгрупповую дисперсию получают путём расчёта суммы квадратов отклонения математических ожиданий выборок от общего математического ожидания, отнесённую к числу выборок за вычетом 1. Затем проверяют “нуль-гипотезу” - предположение, что всё изменение параметра оптимизации никак не связано с изменением фактора, то есть, математические ожидания внутри выборок равны (за исключением погрешностей единичных опытов), для чего относят межгрупповую дисперсию к внутригрупповой, получая критерий Фишера, который сравнивают с табличным, опровергая (или подтверждая) нуль-гипотезу. Многофакторный дисперсионный анализ, помимо оценки влияния каждого фактора на параметр оптимизации в отдельности, позволяет также установить наличие или отсутствие взаимного факторов на параметр оптимизации.
Практическая работа № 3 Содержание отчёта Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить расчёт внутригрупповых и межгрупповых сумм квадратов отклонений, а также дисперсий, расчёт критерия Фишера, привести табличноеего значение или непосредственно вероятность принятия (или опровержения) нуль-гипотезы. В качестве вывода следует указатьналичие, отсутствие или незначимость (малую значимость) влияния фактора на параметр оптимизации.
Вопросы для самоконтроля 1. В чём состоит задача дисперсионного анализа? 2. Чем отличаются однофакторный и многофакторный дисперсионный анализ? 3. Укажите достоинства и недостаткииспользования дисперсионного анализа для оценки значимости влияния факторов на параметр оптимизации по сравнению с другими методами, позволяющими выполнить эту задачу. 4. Какие требования предъявляются (не предъявляются) к значениям факторов в дисперсионном анализе? 5. Что такое критерий Фишера? Для чего его используют в дисперсионном анализе? Задание для работы Задание для работы приведено в таблице 3.1.
Таблица 3.1 – Задание для работы.
Полусфера | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | 86 | 86 | 88 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | 87 | 85 | 89 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | 86 | 86 | 87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | 88 | 87 | 88 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | 87 | 86 | 87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Буферность солёной сельди, град. | Вид разделки | Неразделанная | Обезглавленная | Б/г потрошёная |
Филе-кусочки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | 140 | 110 | 80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 145 | 135 | 100 | 85 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 135 | 125 | 125 | 95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | 130 | 110 | 100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 145 | 135 | 105 | 80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Выход солёной рыбы, % | Способ посола | Сухой обычный | Смешанный | Тузлучный |
Сухой стоповый | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | 102 | 103 | 87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | 100 | 102 | 91 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | 103 | 104 | 88 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | 101 | 103 | 89 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | 100 | 100 | 88 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Альдегиднгое число жира (при морозильном хранении) | Вид упаковки | Отсутствует | Полиэтиленовая плёнка (без вакуума) | Полиэтиленовая плёнка (вакуум) | Картон | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10,1 | 8,2 | 3,3 | 8,3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9,8 | 7,1 | 2,9 | 7,8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11,3 | 6,9 | 3,6 | 8,5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8,9 | 7,8 | 3,8 | 7,6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9,6 | 7,5 | 3,0 | 8,2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Доля отслаивающегося жира (в паштетных консревах), % | Содержание яичного порошка в рецептуре, % | 0 | 0,5 | 1 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 3 | 1 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 2 | 2 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 3 | 0 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | 1 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 2 | 2 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Продолжение таблицы 3.1
| 6 | Усилие резания, гс | Дозировка крахмала в рецептуре, г/100 г мясного сырья | 0 | 1 | 3 | 4 |
| 200 | 210 | 230 | 210 | |||
| 220 | 230 | 220 | 230 | |||
| 180 | 240 | 210 | 220 | |||
| 240 | 210 | 230 | 210 | |||
| 190 | 200 | 240 | 230 | |||
| 7 | Пористость пирожков с мясной начинкой, % | Температура во второй период выпечки, ºС | 180 | 200 | 210 | 220 |
| 75 | 76 | 77 | 76 | |||
| 77 | 78 | 79 | 77 | |||
| 75 | 77 | 78 | 76 | |||
| 78 | 78 | 76 | 77 | |||
| 77 | 76 | 77 | 78 | |||
| 8 | Усилие резания, гс | Вид панировки котлет | Отсутствует | Мука | Сухари | Мука плюс сухари |
| 430 | 320 | 280 | 270 | |||
| 460 | 340 | 260 | 280 | |||
| 430 | 330 | 290 | 290 | |||
| 450 | 310 | 300 | 270 | |||
| 440 | 320 | 290 | 290 | |||
| 9 | Конечная влажность вяленой рыбы | Характеристика периодов «отдыха» | Отсутствуют | 0,5 часа каждые 4 часа | 1 час каждые 4 часа | 2 часа каждые 4 часа |
| 48 | 46 | 44 | 48 | |||
| 49 | 48 | 45 | 49 | |||
| 52 | 46 | 46 | 51 | |||
| 48 | 48 | 47 | 49 | |||
| 49 | 47 | 45 | 50 | |||
| 10 | Температура в центре мяса (при варке)
| Добавление специй | Нет | Перец чёрный | Перец душистый | Лавровый лист |
| 78 | 79 | 80 | 79 | |||
| 79 | 78 | 79 | 77 | |||
| 76 | 77 | 78 | 78 | |||
| 80 | 79 | 76 | 79 | |||
| 79 | 78 | 77 | 78 |
Практическая работа № 4
Планирование двухфакторного эксперимента и обработка данных
Цель работы: научиться составлять центральный композиционный ротатабельный план, проводить эксперимент и обрабатывать данные методом линейной регрессии.
Задачи:
1. Получить задание в виде наименования технологического процесса, факторов и параметра оптимизации, а также имитационную модель (программу) для получения экспериментальных данных.
2. Выбрать уровни варьирования факторов и составить центральный композиционный ротатабельный план.
3. Провести рандомизацию составленного плана
4. Провести модельный эксперимент (последовательно ввести данные в программу)
5. С использованием средств Excel (LOCalc) провести регрессионный анализ по линейной и сведённой к линейной квадратичной моделям.
6. Сделать вывод о результатах
Ход работы
Обучающиеся получают задание, включающее наименование оптимизируемого процесса, предлагаемые факторы и параметр оптимизации (с направлением оптимизации) и их естественные границы. Задание представлено в виде специальной программы (exe-файла под Windows или бинарного файла в формате ELF под linux). Этот же файл является имитационной моделью, т.е. способен генерировать значения параметра оптимизации для заданных факторов. Модель носит учебный характер и не отражает точно реальный процесс, для исследовательских целей её использовать нельзя. Типовая имитационная модель представлена программой, написанной на языке FreePascalв среде Lazarus (Приложение В). При постановке курса преподаватель разрабатывает и/или частично изменяет модели под группу обучающихся.
Первая задача обучающихся – провести нормализацию факторов (см. ПР № 3), т.е. написать формулу, переводящую любое значение каждого фактора (параметра) в нормализованное значение, а также рассчитать пограничные значения. Для факторов следует предположить, что они будут использованы в ЦКРП, т.е. рассчитать значения исходных факторов, соответствующие нормализованным–1; 0; +1; 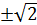 .
.
Далее обучающиеся заполняют указанные уровни в таблицу (табл.1) в MSExcel или LOCalc, после чего проводят рандомизацию. Рандомизированный план эксперимента реализуют на имитационной модели (в программе) построчно, перенося результат в таблицу.
Регрессионный анализ проводят с помощью Excel; результаты оформляют в виде уравнения регрессии, критерия Фишера. По критерию Фишера оценивают адекватность квадратичной модели.
Содержание отчёта
Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить план и результаты эксперимента, результаты регрессионного анализа по линейной и квадратичной (сведённой к линейной) модели. В качестве вывода следует указать адекватность линейной и квадратичной моделей, а также привести их.
Вопросы для самоконтроля
1. Что такое полный факторный эксперимент 22? Сколько опытов он включает?
2. Что включает в себя центральный композиционный ротатабельный план? Для чего его следует использовать?
3. Что такое регрессионный анализ? Для чего его можно использовать?
4. Какие требования к числу опытов в исходной выборке представляют в регрессионном анализе? Что такое число степеней свободы?
5. Как и для чего используют критерий Фишера в регрессионном анализе?
6. Как произвести сведение нелинейной модели к линейной?
Практическая работа № 5
Поиск значимых факторов с помощью плана Плакетта-Бермана
Цель работы: Изучить всю цепочку поиска оптимума модельного эксперимента.
Задачи:
1. Найти незначимые факторы с помощью плана Плакетта-Бермана и программы VVFreeStat (http://vvfstat.sf.net).
2. Провести и обработать эксперимент в соответствии с ЦКП.
3. Провести поиск оптимума функции с использованием программы Maxima.
Ход работы
Последовательность действий:
1. Получите задание в виде файла – имитационной модели (Приложение Г). В данной работе задание будет абстрактным.
2. Составьте план Плакетта-Бермана по заданию, проведите рандомизацию и рассчитайте значения отклика для каждой строчки с помощью имитационной модели.
3. Введите план и результаты в таблицу программы FreeStat, сохраните данные, вставьте их в отчёт и запустите обработку шаблонов. Шаблоны, в основном, будут линейными. Результаты из правого окна поместите в отчёт.
4. Выявите наиболее значимо влияющие факторы (два). В сомнительных случаях сначала отбросьте самые незначимые, удалите соответствующие им столбцы и повторите обработку.
5. Для указанных факторов составьте центральный композиционный ротатабельный план, проведите рандомизацию и получите результаты. В программе-имитационной модели на место остальных факторов вводите любые значения.
6. Внесите план и результаты в отчёт и в программу FreeStat. Обработайте данные, выбрав оптимизационные шаблоны. Проработайте наилучший из них. Результаты из правого поля вывода перенесите в отчёт.
7. В том же окне постройте график полученного уравнения регрессии. Сохраните его в файл и вставьте в отчёт.
8. Проведите оптимизацию полученного уравнения регрессии, найдите оптимум и вставьте его в отчёт. Вставьте в отчёт и последовательность действий для оптимизации.
Содержание отчёта
Обязательные пункты отчета:
1. Название работы
2. План Плакетта-Бермана и значения откликов.
3. Результаты обработки плана; выбранные наиболее значимые факторы.
4. Центральный композиционный ротатабельный план и значения откликов.
5. Результаты обработки: уравнение регрессии с коэффициентами, критерий Фишера; вывод об адекватности модели.
6. График уравнения регрессии.
7. Расчёт экстремума функции
8. Ответ (точка экстремума, при наличии) и вывод.
Факультативные пункты отчёта приведены в практической работе № 1.
Вопросы для самоконтроля
1. Что такое полный дробный факторный эксперимент? Для чего он нужен?
2. Что такое планы Плакетта-Бермана? С какой целью их можно использовать.
3. Как использовать план Плакетта-Бермана с большим количеством факторов, чем имеется?
Практическая работа № 6
Ход работы
Обучающиеся получают задание на расчёт (совпадает с заданием к практической работе № 4). Далее они самостоятельно выбирают исходную точку и составляют в ней ПФЭ (сама исходная точка соответствует уровням варьирования -1; -1), причём диапазон варьирования факторов должен быть небольшим (до 10 % всего интервала варьирования). Результаты, полученные с помощью ПФЭ, обрабатывают статистически (в электронной таблице Excel или LOCalc, в специализированной коммерческой программе OakdaleDatafitили в специализированной бесплатной программе FreeStat–http://vvfstat.sf.net), получают уравнение регрессии и градиент. Затем делают шаг по градиенту, самостоятельно задавая h или h*. В полученной точке строят ПФЭ, рассчитывают значения для каждого опыта в ПФЭ. Шаг считается успешным, если в первой точке ПФЭ значение параметра оптимизации лучше, чем в первой точке предыдущего плана или в любой точке полученного ПФЭ получено наилучшее значение параметра оптимизации, или среднее значение параметра оптимизации по ПФЭ выше среднего значения на предыдущем шаге. Если ни одно из этих условий не выполняется, то возвращаются в исходную точку и делают более короткий (половинный) шаг.
Расчёт заканчивают, если:
- После как минимум одного успешного шага не менее чем за 3 попытки (с делением шага пополам) не удалось сделать успешный шаг.
- ПФЭ достиг границы допустимой зоны изменения факторов обоих, а градиент однозначно указывает за неё. Если за границу выходит только один фактор, его оставляют на границе.
В любом из этих случаев последнюю точку считают центром ЦКРП и проводят окончательную оптимизацию. Интервал варьирования выбирают так, чтобы ни одна из звёздных точек не вышла за допустимую зону изменения факторов. Если этого не наблюдается, то можно принять диапазон варьирования чуть больше, чем диапазон варьирования для ПФЭ.
Пример расчёта.
Вариант № 1, обезвоживание эмульсии[3]. X1 - температура, °C от 25 до 95; X2 - время, мин, от 0 до 60. Параметр оптимизации: Y - степень обезвоживания, % от 0 до 100. Необходимо найти максимум.
Задаёмся точкой X1,1 = 30; X2,1 = 10, строим ПФЭ и рассчитываем значения.
| X1 | X2 | Y |
| 30 | 10 | 4,722029 |
| 30 | 15 | 6,538094 |
| 32 | 10 | 3,614906 |
| 32 | 15 | 6,699179 |
Обработка в среде FreeStat по уравнению регрессии 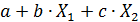 позволила получить коэффициенты регрессии b= –0,20680945; c= 0,490818249. Выбираем h=5, тогда
позволила получить коэффициенты регрессии b= –0,20680945; c= 0,490818249. Выбираем h=5, тогда
X1,2 = 30+(–0,20680945)·5=28,96595275≈29;
X2,2 = 10+ 0,490818249·5=12,45409124≈12,5.
Составляем ПФЭ из этой точки:
| X1 | X2 | Y |
| 29 | 12,5 | 6,595308 |
| 29 | 17,5 | 7,515984 |
| 31 | 12,5 | 6,301609 |
| 31 | 17,5 | 7,556751 |
Следует обратить внимание, что значения Y больше значений в предыдущем плане, поэтому шаг выполнен верно. Проводим обработку во FreeStat по тому же уравнению регрессии, получаем b=0,036649587; c=0,218693721. Таким образом, не изменяя шаг, получаем X1,3 = 28,8; X2,3 =13,6. Проверяем ПФЭ
|
X1 | X2 | Y |
| 28,8 | 13,6 | 6,248606 |
| 28,8 | 18,6 | 7,444726 |
| 30,8 | 13,6 | 6,451096 |
| 30,8 | 18,6 | 8,114149 |
Следует обратить внимание, что результаты, в основном, ухудшились, но в последней точке получен абсолютный максимум. Таким образом, можно принять и этот шаг, продолжив двигаться по градиенту. С другой стороны, можно попытаться отклонить этот шаг, чтобы найти наилучшую точку.
Далее процесс повторяют до условия окончания.Следует обратить внимание, что результаты, в основном, ухудшились, но в последней точке получен абсолютный максимум. Таким образом, можно принять и этот шаг, продолжив двигаться по градиенту. С другой стороны, можно попытаться отклонить этот шаг, чтобы найти наилучшую точку.
Содержание отчёта
Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить таблицы, являющиеся шагами «крутого восхождения»/градиентного спуска. В качестве вывода следует указать найденную точку экстремума.
Вопросы для самоконтроля
1. Что такое градиент? Как его найти?
2. Как найти приближённое значение частной производной, если функция не представлена в аналитическом виде?
3. В чём сущность метода крутого восхождения (градиентного спуска)?
4. Чем необходимо руководствоваться при выборе шага (h)?
Практическая работа № 7
Ход работы
Последовательность действий для изучения:
1. Запустите программу wxMaxima и познакомьтесь с интерфейсом.
2. Проделайте все те операции, которые указаны в теоретических сведениях. Подберите по паре своих примеров на каждую разбираемую операцию, обратите особое внимание на случаи, когда наблюдается нестандартное и/или неожиданное поведение системы.
3. Используя уравнение регрессии, полученное с прошлой работы:
3.1Постройте его трёхмерный график и предположите наличие экстремумов;
3.2Найдите точку, подозрительную на экстремум.
ЧАСТЬ 2. ОПТИМИЗАЦИЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ В СРЕДЕ MAXIMA
Цель работы: Изучить возможности оптимизации функции двух переменных.
Задачи:
1. Научиться определять точку, подозрительную на экстремум
2. Научиться проверять значения на границах интервала варьирования
Ход работы
Последовательность действий:
1. Получите задание в виде функции двух переменных.
2. Запустите программу wxMaxima и определите функцию.
3. Присвойте флагу numer значение true.
4. Найдите частные производные функции, приравняйте их к нулю и решите уравнение командой solve. Поскольку необходимо искать только действительные корни, можно присвоить флагу realonlytrue, но уравнения решать командой algsys, а не solve. При невозможности решения командами solve и algsys воспользуйтесь командой to_poly_solve (команда работает ОЧЕНЬ медленно). Если таким способом решение получить не удаётся, то можно попробовать перед решением системы решить одно уравнение, а потом подставить его во второе.
5. Проверьте значения функции в точках, соответствующих всем действительным решениям (и x, и y не должны содержать %i). Для дальнейшего рассмотрения выберите наибольшее (наименьшее) число. Проверяйте, чтобы x и y находились в границах заданного интервала.
6. Найдите и проверьте экстремумы (точки, подозрительные на экстремум) на следующих срезах, приравняв производные полученных функций к 0:
7. 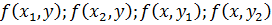
8. Проверяйте, чтобы x и y находились в границах заданного интервала.
9. Определить значения функции в углах диапазона 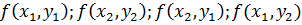
10. Из найденных в пп. 4, 5, 6 точек найдите точку с наибольшим (наименьшем) значением функции и сделайте вывод. В ответ обязательно запишите значения x и y.
11. Постройте трёхмерный графикфункции.
Содержание отчёта
Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить результаты выполнения работы в среде Maxima, допускается прилагать файл, сохранённый в этой среде (.wxmx). В качестве вывода следует указать найденную точку экстремума.
Вопросы для самоконтроля
1. Какие действия необходимо выполнить для проведения безусловной оптимизации аналитическим методом первого порядка в двухфакторной задаче?
2. Что такое системы компьютерной алгебры (символьной математики)? Какие задачи они позволяют решить?
3. Что такое «седловая точка»? Является ли она экстремумом?
Задания для работы
1. 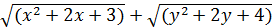 ,
, 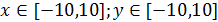 , найти минимум
, найти минимум
2. 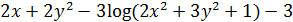 ,
, 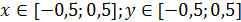 , найти максимум
, найти максимум
3. 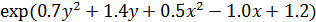 ,
, 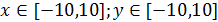 , найти минимум
, найти минимум
4. 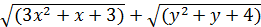 ,
, 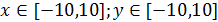 , найти минимум
, найти минимум
5. 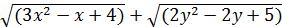 ,
,

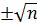 .
.


