Понятие об условной оптимизации

 

Условная оптимизация – оптимизация целевой функции при выполнении определённых условий, что математически можно представить следующим образом:

…

Если функции f, g, q … носят линейный характер относительно всех факторов, то такая задача и её решение называют линейным программированием. Для решения таких задач чаще всего используют симплекс-метод.

Если целевая функция f носит нелинейный характер, то такую задачу называют нелинейным программированием.

Одним из способов решения задач линейного и, в ряде случаев, нелинейного программирования является метод неопределённых множителей Лагранжа.

 

Практическая работа № 9

 Оптимизация методом неопределенных множителей Лагранжа

 

Цель работы: изучить метод условной оптимизации с помощью множителей Лагранжа.

Задачи:

1. Получить задание в виде целевой функции и ряда условий.

2. Составить функцию Лагранжа.

3. Найти частные производные функции Лагранжа по факторам и множителям Лагранжа и приравнять их к нулю.

4. Решить систему уравнений (самостоятельно или в Maxima).

5. Найти оптимум.

Краткие теоретические сведения

    Метод неопределённых множителей Лагранжа позволяет решать задачи условной оптимизации, если условия заданы в виде равенств. Эти условия могут накладывать дополнительные ограничения на значения целевой функции, ограничивая точки нахождения возможных оптимумов. Вариантами таких условий является постоянная сумма факторов (например, при оптимизации рецептуры сумма всех ингредиентов должна составлять 100 %); сумма квадратов факторов, равняющаяся некоторому числу (все решения должны находиться на окружности/сфере/гиперсфере). Возможны и другие условия оптимизации; их может быть несколько. Таким образом, задача имеет общий вид

………………….

    Функцию Лагранжа записывают следующим образом:

    Далее необходимо найти частные производные функции F по факторам и множителям λ, первые n[5] из которых будут содержать как производные целевой функции, так и значения неопределённых множителей λ, а остальные фактически будут заданными условиями. Частные производные приравнивают к нулю, получая систему уравнений. Среди решения системы должен быть заданный оптимум, который проверяют по исходной целевой функции.

 

Ход работы

Задание включает в себя математическое выражение целевой функции и ряд условий. Необходимо записать функцию Лагранжа, получить частные производные (самостоятельно или через систему Maxima), приравнять их к нулю и решить систему уравнений. Среди множества решений следует выбрать один наиболее оптимальный. Следует помнить, что решениями системы будут и минимумы, и максимумы (если таковые имеются), а также локальные экстремумы в случае сложных функций.

Пример расчёта

Задание: найти минимум  при

Решение.

Сначала вводим данные в систему Maxima и определяем функцию Лагранжа:

Составляем систему уравнений из частных производных функции Лагранжа

 

Решаем полученную систему, присваивая некоторой переменной значения

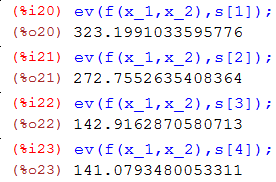
Проверяем 4 полученных решения:

Таким образом, четвёртое решение является минимумом, т.е.

На всякий случай строим график целевой функции

Содержание отчёта

Общие требования к содержанию отчёта приведены в рамках практической работы № 1В данной работе в разделе «ход работы» необходимо представить результаты выполнения работы в среде Maxima, допускается прилагать файл, сохранённый в этой среде (.wxmx). В качестве вывода следует указать найденную точку оптимума.

Вопросы для самоконтроля

1. Что такое условная оптимизация?

2. Приведите примеры условий в условной оптимизации в отрасли.

3. В чём отличия линейного и нелинейного программирования?

4. В чём сущность метода неопределённых множителей Лагранжа?

Задания для работы

1. Найти минимум  при .

2. Найти максимум -  при .

3. Найти минимум 5  при .

4. Найти максимум  при .

5. Найти минимум 5  при

6. Найти максимум  при .

7. Найти минимум  при

8. Найти максимум -  при .

9. Найти минимум 5  при .

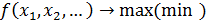
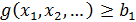
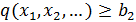
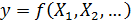
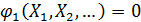
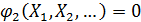
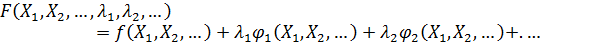
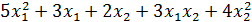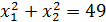
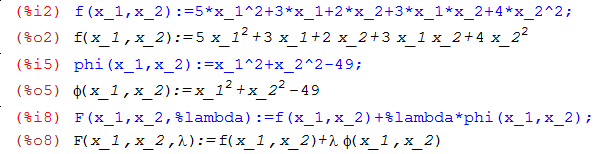
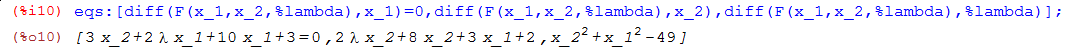
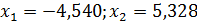
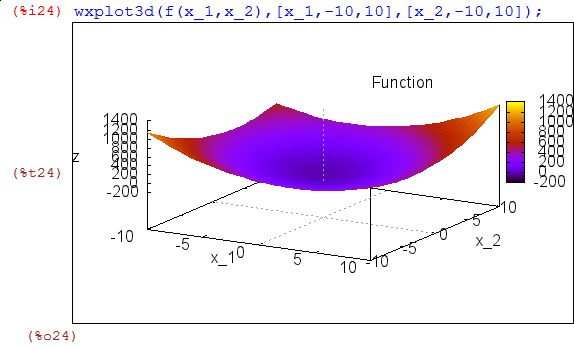
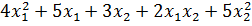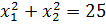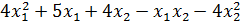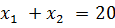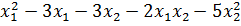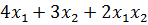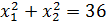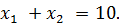
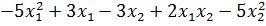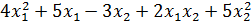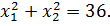
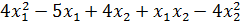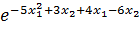10. Найти максимум  при 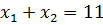.