
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация методом «крутое восхождение»Содержание книги
Поиск на нашем сайте
Цель работы: изучить оптимизацию методом «крутого восхождения». Задачи: 1. Получить задание (см практическую работу № 6). 2. Выбрать диапазон изменения факторов, скорость движения по градиенту. 3. Провести с использованием ПФЭ движение по градиенту. 4. Провести поиск оптимума функции с помощью ЦРКП. Краткие теоретические сведения Метод «крутого восхождения» или градиентного спуска основан на определении градиента функции и последующего движения по нему. В этом методе проводят планирование эксперимента в узком диапазоне варьирования факторов. В исходной точке необходимо определить градиент, для чего целесообразно использовать либо полный, либо дробный факторный эксперимент (для двух факторов использование дробного факторного эксперимента нецелесообразно). Далее проводят движение по градиенту (при поиске максимума) или против него (для минимума). Шаг для движения либо выбирают пропорционально градиенту (но это может привести к шагу далеко за оптимум), либо задаются им изначально. Значение градиента можно получить через уравнение регрессии. Например, если уравнение регрессии имеет вид
то градиент будет равен Движение по градиенту (поиск максимума) можно провести, определив точку
где h – шаг по градиенту. В случае, если шаг задан изначально (h *), то При необходимости движения против градиента (поиск минимума)
В полученной точке необходимо проверить значение параметра оптимизации y. Если он ближе к оптимальному, то движение по градиенту можно продолжить. В противном случае шаг по градиенту (против градиента) следует считать неудачным. Решить проблему можно либо путём уменьшения шага, либо использованием метода «оврагов», либо прекратив движение по градиенту, приступая к ЦКРП.
Ход работы Обучающиеся получают задание на расчёт (совпадает с заданием к практической работе № 4). Далее они самостоятельно выбирают исходную точку и составляют в ней ПФЭ (сама исходная точка соответствует уровням варьирования -1; -1), причём диапазон варьирования факторов должен быть небольшим (до 10 % всего интервала варьирования). Результаты, полученные с помощью ПФЭ, обрабатывают статистически (в электронной таблице Excel или LOCalc, в специализированной коммерческой программе OakdaleDatafitили в специализированной бесплатной программе FreeStat–http://vvfstat.sf.net), получают уравнение регрессии и градиент. Затем делают шаг по градиенту, самостоятельно задавая h или h*. В полученной точке строят ПФЭ, рассчитывают значения для каждого опыта в ПФЭ. Шаг считается успешным, если в первой точке ПФЭ значение параметра оптимизации лучше, чем в первой точке предыдущего плана или в любой точке полученного ПФЭ получено наилучшее значение параметра оптимизации, или среднее значение параметра оптимизации по ПФЭ выше среднего значения на предыдущем шаге. Если ни одно из этих условий не выполняется, то возвращаются в исходную точку и делают более короткий (половинный) шаг. Расчёт заканчивают, если: - После как минимум одного успешного шага не менее чем за 3 попытки (с делением шага пополам) не удалось сделать успешный шаг. - ПФЭ достиг границы допустимой зоны изменения факторов обоих, а градиент однозначно указывает за неё. Если за границу выходит только один фактор, его оставляют на границе. В любом из этих случаев последнюю точку считают центром ЦКРП и проводят окончательную оптимизацию. Интервал варьирования выбирают так, чтобы ни одна из звёздных точек не вышла за допустимую зону изменения факторов. Если этого не наблюдается, то можно принять диапазон варьирования чуть больше, чем диапазон варьирования для ПФЭ.
Пример расчёта. Вариант № 1, обезвоживание эмульсии[3]. X1 - температура, °C от 25 до 95; X2 - время, мин, от 0 до 60. Параметр оптимизации: Y - степень обезвоживания, % от 0 до 100. Необходимо найти максимум. Задаёмся точкой X1,1 = 30; X2,1 = 10, строим ПФЭ и рассчитываем значения.
Обработка в среде FreeStat по уравнению регрессии X1,2 = 30+(–0,20680945)·5=28,96595275≈29; X2,2 = 10+ 0,490818249·5=12,45409124≈12,5. Составляем ПФЭ из этой точки:
Следует обратить внимание, что значения Y больше значений в предыдущем плане, поэтому шаг выполнен верно. Проводим обработку во FreeStat по тому же уравнению регрессии, получаем b=0,036649587; c=0,218693721. Таким образом, не изменяя шаг, получаем X1,3 = 28,8; X2,3 =13,6. Проверяем ПФЭ
Следует обратить внимание, что результаты, в основном, ухудшились, но в последней точке получен абсолютный максимум. Таким образом, можно принять и этот шаг, продолжив двигаться по градиенту. С другой стороны, можно попытаться отклонить этот шаг, чтобы найти наилучшую точку. Далее процесс повторяют до условия окончания.Следует обратить внимание, что результаты, в основном, ухудшились, но в последней точке получен абсолютный максимум. Таким образом, можно принять и этот шаг, продолжив двигаться по градиенту. С другой стороны, можно попытаться отклонить этот шаг, чтобы найти наилучшую точку. Содержание отчёта Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить таблицы, являющиеся шагами «крутого восхождения»/градиентного спуска. В качестве вывода следует указать найденную точку экстремума. Вопросы для самоконтроля 1. Что такое градиент? Как его найти? 2. Как найти приближённое значение частной производной, если функция не представлена в аналитическом виде? 3. В чём сущность метода крутого восхождения (градиентного спуска)? 4. Чем необходимо руководствоваться при выборе шага (h)?
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.215 (0.009 с.) |

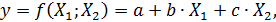
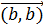
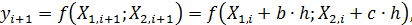
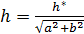
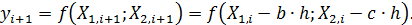
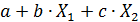 позволила получить коэффициенты регрессии b= –0,20680945; c= 0,490818249. Выбираем h=5, тогда
позволила получить коэффициенты регрессии b= –0,20680945; c= 0,490818249. Выбираем h=5, тогда


