
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведенияСодержание книги
Поиск на нашем сайте Полный факторный эксперимент 2n является достаточным для изучения общих тенденций, но недостаточным для подробного исследования функции отклика. Для его расширения следует использовать композиционные планы, в т.ч. центральный композиционный ротатабельный план (табл. 4,5) Опыты в центре плана могут повторяться. Как правило, окончательный план эксперимента записывают в ненормированных значениях факторов. Перед проведением эксперимента план, как правило, подвергают рандомизации – т.е. меняют местами строки в случайном порядке. После проведения эксперимента используют статистические методы обработки данных, прежде всего, регрессионный анализ. Регрессионный анализ (только линейную регрессию) можно проводить в Excel. Для этого можно либо воспользоваться пакетом «Анализ данных» (на вкладке «Данные»), либо функцией ЛИНЕЙН. Так как функция возвращает массив результатов, то её надо вводить соответствующим образом: запись можно начинать, только выделив пустой диапазон. Ширина диапазона должна быть равна числу всех факторов (m)+1, а высота – ровно 5 клеток. Первым параметром функции служит массив факторов (собственно план эксперимента), вторым – столбец со значениями параметра оптимизации. Для получения дополнительных данных (в т.ч. значения критерия Фишера) третий и четвёртый параметры должны иметь значение ИСТИНА (третий можно установить в ЛОЖЬ, если есть основания полагать, что свободный член
Будет получена следующая таблица данных (никаких подписей и комментариев Excel не предоставляется):
где Однако линейная регрессия не подходит для последующего поиска оптимума, поэтому необходимо свести к линейной, как минимум, квадратичную регрессию. Для этого к двум факторам добавляют следующие столбцы: Тем не менее, нужно помнить и недостатки регрессионного анализа в среде Excel. Во-первых, не все сложные модели легко сводятся к линейным. Во-вторых, Excel не позволяет построить трёхмерный график соответствия. В-третьих, для проверки значимости коэффициентов регрессии требуются дополнительные расчёты. Ход работы Обучающиеся получают задание, включающее наименование оптимизируемого процесса, предлагаемые факторы и параметр оптимизации (с направлением оптимизации) и их естественные границы. Задание представлено в виде специальной программы (exe-файла под Windows или бинарного файла в формате ELF под linux). Этот же файл является имитационной моделью, т.е. способен генерировать значения параметра оптимизации для заданных факторов. Модель носит учебный характер и не отражает точно реальный процесс, для исследовательских целей её использовать нельзя. Типовая имитационная модель представлена программой, написанной на языке FreePascalв среде Lazarus (Приложение В). При постановке курса преподаватель разрабатывает и/или частично изменяет модели под группу обучающихся. Первая задача обучающихся – провести нормализацию факторов (см. ПР № 3), т.е. написать формулу, переводящую любое значение каждого фактора (параметра) в нормализованное значение, а также рассчитать пограничные значения. Для факторов следует предположить, что они будут использованы в ЦКРП, т.е. рассчитать значения исходных факторов, соответствующие нормализованным–1; 0; +1; Далее обучающиеся заполняют указанные уровни в таблицу (табл.1) в MSExcel или LOCalc, после чего проводят рандомизацию. Рандомизированный план эксперимента реализуют на имитационной модели (в программе) построчно, перенося результат в таблицу. Регрессионный анализ проводят с помощью Excel; результаты оформляют в виде уравнения регрессии, критерия Фишера. По критерию Фишера оценивают адекватность квадратичной модели. Содержание отчёта Общие требования к содержанию отчёта приведены в рамках практической работы № 1. В данной работе в разделе «ход работы» необходимо представить план и результаты эксперимента, результаты регрессионного анализа по линейной и квадратичной (сведённой к линейной) модели. В качестве вывода следует указать адекватность линейной и квадратичной моделей, а также привести их. Вопросы для самоконтроля 1. Что такое полный факторный эксперимент 22? Сколько опытов он включает? 2. Что включает в себя центральный композиционный ротатабельный план? Для чего его следует использовать? 3. Что такое регрессионный анализ? Для чего его можно использовать? 4. Какие требования к числу опытов в исходной выборке представляют в регрессионном анализе? Что такое число степеней свободы? 5. Как и для чего используют критерий Фишера в регрессионном анализе? 6. Как произвести сведение нелинейной модели к линейной?
Практическая работа № 5 Поиск значимых факторов с помощью плана Плакетта-Бермана Цель работы: Изучить всю цепочку поиска оптимума модельного эксперимента. Задачи: 1. Найти незначимые факторы с помощью плана Плакетта-Бермана и программы VVFreeStat (http://vvfstat.sf.net). 2. Провести и обработать эксперимент в соответствии с ЦКП. 3. Провести поиск оптимума функции с использованием программы Maxima.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

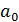 отсутствует, т.е. при нулевых значениях факторов параметр оптимизации точно должен равняться нулю). По окончании ввода надо нажимать не Enter, а Ctrl+Shift+Enter. Для линейной модели регрессии вида
отсутствует, т.е. при нулевых значениях факторов параметр оптимизации точно должен равняться нулю). По окончании ввода надо нажимать не Enter, а Ctrl+Shift+Enter. Для линейной модели регрессии вида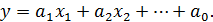
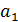
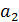
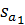
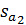
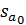
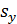
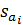 – среднеквадратическое отклонение коэффициента регрессии, R2 – коэффициент детерминации,
– среднеквадратическое отклонение коэффициента регрессии, R2 – коэффициент детерминации, 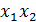 ;
; 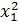 ;
; 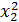 .
.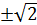 .
.


