Постановка задач оптимизации. Их классификация.

Здесь можно сразу выделить два класса оптимизационных задач: задачи безусловной оптимизации, когда решение можно искать на всем множестве действительных чисел и задачи условной оптимизации, когда на область допустимых решений накладываются определенные ограничения - условия, и формируется так называемая область допустимых решений. Первый класс задач - это задачи исследования функций на максимум-минимум, которое осуществляется с помощью производной. Ко второму классу относятся задачи так называемого математического программирования. Считается, что необходимым и достаточным условием для постановки задач условной оптимизации систем является задание: а) критерия оптимизации q = F(X) ® min (max), т.е. показателя или параметра, в экстремуме которого заинтересован исследователь; б) целевой функции F(X), связывающей критерий с переменными xj (j = 1 …n), т.е. теми конструктивными и другими характеристиками системы, которые могут быть изменены при необходимости; в) ограничений Аij(Xj) ³ bi (i = 1 …m), на ряд характеристик, также являющихся функциями xj; г) области значений учитываемых переменных x_j^min £ x_j £ x_j^max. Принципиальная возможность строгой постановки задач оптимизации возникает лишь при аналитическом выражении критерия оптимизации q и функций ограничений A_i(X_j). Ограничения в задачах оптимизации могут касаться: - доступных ресурсов (средств, времени); - природы рассматриваемых процессов и учитываемых переменных; -особенностей принятия допущений и области значений переменных. Последовательность решения оптимизационных задач в обычно включает следующие этапы: 1.содержательная (вербальная) постановка; 2.составление математической (числовой) модели; 3.подготовка исходных данных по каждому из альтернативных воздействий и определение области допустимых решений; 4.выбор метода решения задачи; 5.разработка или подбор алгоритма (программы) вычислений вручную или на ЭВМ; 6.решение задачи, т.е. нахождения оптимума - максимального или минимального значения целевой функции (критерия); 7.верификация, т.е. проверка полученных результатов на правдоподобность и анализ решения.

Нечеткие множества и их использование для принятия решений.

В работе Беллмана и Заде впервые было предложено использовать теорию нечетких множеств в качестве аппарата для решения задачи оптимального выбора.Обычно при ее решении делаются следующие упрощения: независимость выбора от состояний среды (закрытые системы), одинаковая важность критериев, каждая целеваяфункция определяет отношение полного порядка на множестве объектов.Пусть E – множество объектов, оцениваемых по множеству критериев K; Xi –область, в которой оцениваются объекты по критерию KiЄK. Целевая функция, связываемая с критерием Ki, описывается нечетким множеством Gi, определенным на Xi с функцией принадлежности μ_Gi(x). Значение μ_Gi(x)=1 (ядро множества) соответствует полной совместимости оценки x с множеством целей Gi, а μ_Gi(x)=0 - полной несовместимости. Значения μ>0 (носитель нечеткого множества Gi) соответствует частичной совместимости значений оценки и целей, задаваемыхпредпочтениями ЛПР. Определение величин μ_Gi(x)может осуществляться различными методами, например: использование градаций уровня совместимости (т.е.дискретизация множества X), их сопоставление с оценками ЛПР по лингвистической шкале с последующим сглаживанием дискретных значений; представление нечеткой цели в виде нечеткого числа, причем ЛПР непосредственно задает параметры модели, исходя из имеющейся информации и своих предпочтений.После того, как функции μ_Gi(x)построены для всех целей, решается задача их свертки, которая формулируется в следующем виде: имеется m частных целей,связываемых с m критериями Ki, по которым оцениваются объекты из множества E.Нечеткое множество объектов, совместимых с общей целью, получается свертыванием нечетких множеств с функциями принадлежности μ_Gi(x). Иными словами ищется

отображение f из [0, 1]^m в [0,1] такое, что μ_∑=f(μ1,...,μ m)

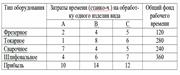
Условная оптимизация. Линейное программирование. Пример постановки задачи оптимизации.

Пример постановки задачи оптимизации.

Для изготовления 3-х видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия приведены в таблице.

Определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи. Решение: Пусть будет изготовлено Х₁ единиц изделия А Х₂ единиц изделия В Х₃ единиц изделия С. Тогда при использовании фрезерного оборудования потребуется затратить 2Х₁ + 4Х₂ + 5Х₃ станко-часов. Но по условию ограничения общего фонда времени 2Х₁ + 4Х₂ + 5Х₃ £ 120. Аналогично для токарного, сварочного и шлифовального оборудования: 1)Х₁ + 8Х₂ + 6Х₃ £ 280 2)7Х₁ + 4Х₂ + 5Х₃ £ 240 3)4Х₁ + 6Х₂ + 7Х₃ £ 360 При этом, т.к. количество изготовляемых деталей не может быть отрицательным, то Х₁ ³ 0, Х₂ ³ 0, Х₃ ³ 0. Далее, если будет изготовлено Х₁ изделий А, Х₂ изделий В и Х₃ изделий С, то прибыль от их реализации составит F = 10Х₁ + 14Х₂ + 12Х₃ Итак, мы получаем систему четырех линейных неравенств с тремя неизвестными (X_j (j = 1…3): 1)2Х₁ + 4Х₂ + 5Х₃ £ 120 2)Х₁ + 8Х₂ + 6Х₃ £ 280 3)7Х₁ + 6Х₂ + 7Х₃ £ 360 Х₁ ³ 0, Х₂ ³ 0, Х₃ ³ 0. И линейную функцию F = 10Х₁ + 14Х₂ + 12Х₃ относительно этих же переменных. Требуется среди всех неотрицательных решений системы неравенств найти такое, при котором целевая функция F принимает максимальное значение. Постановка задачи линейного программирования Найти оптимум (наибольшее или наименьшее значение) целевой функции (линейной формы) на области допустимых значений системы ограничений при наличии дополнительных условий неотрицательности переменных х_j ³ 0, j = 1,…, n. Если в системе ограничений l = m, т.е. она состоит только из уравнений, то соответствующая форма записи называется канонической.