Искусственные нейронные сети.

Искусственный нейрон (Математический нейрон Маккалока — Питтса, Формальный нейрон) — узел искусственной нейронной сети, являющийся упрощённой моделью естественного нейрона. Математически, искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента — линейной комбинации всех входных сигналов. Данную функцию называют функцией активации или функцией срабатывания, передаточной функцией. Полученный результат посылается на единственный выход. Такие искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других. Искусственные нейроны и сети являются основными элементами идеального нейрокомпьютера.

Схема искусственного нейрона
1.Нейроны, выходные сигналы которых поступают на вход данному
2.Сумматор входных сигналов
3.Вычислитель передаточной функции
4.Нейроны, на входы которых подаётся выходной сигнал данного
5. w_i — веса входных сигналов

Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.

ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.

 

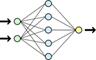
Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым — выходной элемент.

В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. В многослойных нейронных сетях (их часто называют персептронами) нейроны объединяются слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. В общем случае сеть состоит из нескольких слоев, пронумерованных слева на право. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько так называемых скрытых слоев.

Алгоритмы обучения бывают 3-х видов:

Обучение с учителем. При этом сети предъявляется набор обучающих примеров. Каждый обучающий пример представляют собой пару: вектор входных значений и желаемый выход сети. Скажем, для обучения предсказанию временных рядов это может быть набор нескольких последовательных значений ряда и известное значение в следующий момент времени. В ходе обучения весовые коэффициенты подбираются таким образом, чтобы по этим входам давать выходы максимально близкие к правильным.

Обучение с поощрением. При этом сети не указывается точное значение желаемого выхода, однако, ей выставляется оценка хорошо она поработала или плохо.

Обучение без учителя. Сети предъявляются некоторые входные векторы и в ходе их обработки в ней происходят некоторые процессы самоорганизации, приводящие к тому, что сеть становиться способной решать какую-то задачу.

1.

Статистические методы принятия решений.

Процедура принятия решений

Для решения слабо структурированных проблем используется методология системного анализа, системы поддержки принятия решений (СППР). Рассмотрим технологию применения системного анализа к решению сложных задач.

Процедура принятия решений включает следующие основные этапы:

1. формулировка проблемной ситуации;

2. определение целей;

3. определение критериев достижения целей;

4. построение моделей для обоснования решений;

5. поиск оптимального (допустимого) варианта решения;

6. согласование решения;

7. подготовка решения к реализации;

8. утверждение решения;

9. управление ходом реализации решения;

10. проверка эффективности решения.

Для многофакторного анализа, алгоритм можно описать и точнее:

1. описание условий (факторов) существования проблем, И, ИЛИ и НЕ связывание между условиями;

2. отрицание условий, нахождение любых технически возможных путей. Для решения нужен хотя бы один единственный путь. Все И меняются на ИЛИ, ИЛИ меняются на И, а НЕ меняются на подтверждение, подтверждение меняется на НЕ-связывание;

3. рекурсивный анализ вытекающих проблем из найденных путей, т.е. п.1 и п.2 заново для каждой подпроблемы;

4. оценка всех найденных путей решений по критериям исходящих подпроблем, сведенным к материальной или иной общей стоимости.

Предполагается, что некоторый объект может находиться в двух состояниях: S₀ и S₁ с вероятностью q и p соответственно. p=1- q – полная группа событий.

Задана функция распределения (условная):

-объект находится в состоянии S₀

-объект находится в состоянии S₁

Что будет если ошибемся? ® вводится матрица потерь = матрица платы за ошибки.

Н₀ – гипотеза о том, что объект находится в состоянии S₀

Н₁ – гипотеза о том, что объект находится в состоянии S₁

g₀ – решение о том, что объект находится в состоянии S₀

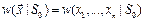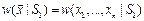g₁ – решение о том, что объект находится в состоянии S₁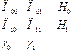

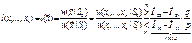- отношение правдоподобия сравнивается с порогом