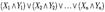Функциональные схемы (лог.диаграммы)

Построение лог.схем И-НЕ. И-НЕ-это схема И и схема НЕ,сложенные вместе.Операция, которую производит такой элемент называется инверсией логического умножения или отрицанием логического умножения, ну или инверсией конъюнкции и еще штрихом Шеффера.Таблица истинности для него: x2 x1 y

0 0 1

0 1 1

1 0 1

1 1 0

Сначала умножаем (логически),а потом все это отрицаем (тоже логически).Если к эл-ту И прилепить на выход инвертор, то получим такой вот элемент И-НЕ.Представл-е ф-ции в задан.базисе.Необх-мо(И-НЕ, ИЛИ-НЕ):1)выд-ть послед.операцию.Если она не соотв-т зад.базису,то необх-мо ее преобр-ть при помощи двойного отрицания,не измен-щего знач-я ф-ции;2)выд-ть предпосл.операцию. Произвести преобр-я аналогично предыдущему и т.д.до исчерпания всех операций.Построение схемы в зад.базисе (общ.алгоритм): 1)для исх.конеч.ф-ций истинности;2)по табл.истинности составляем карты Карно;3)мин.логич. выраж-е для зад.ф-ции;4)разраб-ем схему в соответствии с пред.алг-тмом.

11)Построение лог.схем ИЛИ-НЕ. Операция,выполняемая эл-том ИЛИ-НЕ наз-ся инверсией лог.сложения или инверсией дизъюнкции и еще стрелкой Пирса.Табл.истинности:

x2 x1 y

0 0 1

0 1 0

1 0 0

1 1 0

Если к выходу эл-та ИЛИ-НЕ прилепить инвертор,то пол-ся эл-т ИЛИ.Представление ф-ции в зад.базисе.Необх-мо(И-НЕ, ИЛИ-НЕ):1)выд-ть послед. операцию.Если она не соотв-т зад.базису,то необх-мо ее преобр-ть при помощи двойного отрицания,не изменяющего знач-я ф-ции;2)выд-ть предпосл.операцию. Произвести преобр-я аналогично предыдущему и т.д.до исчерпания всех операций.Построение схемы в зад.базисе (общ.алгоритм):1)для исх.конеч.ф-ций истинности;2)по табл.истинности составляем карты Карно;3)мин.логич.выраж-е для зад.ф-ции;4)разраб-ем схему в соответствии с пред.алгоритмом.

12)Операция ИСКЛ-ИЛИ. Операция,выполняемая таким эл-том наз-ся сложение по модулю 2.Читается это, как "либо икс один, либо икс два".Таблица истинности:

x2 x1 y

0 0 0

0 1 1

1 0 1

1 1 0

 

5. Карты Карно - граф.способ минимизации переключат-х ф-ций обеспечивающий относительную простоту работы с большими выраж-ми и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения.Карты Карно рассматр-ся как перестроенная соответствующим образом таблица истинности ф-ции.Карты Карно были изобретены Эдвардом В. Вейч’ем и усовершенствованы Морисом Карно и были призваны помочь упростить цифр.электр.схемы.В карту Карно булевы переменные перед-ся из табл.истин-ти и упоряд-ся с помощью кода Грея,в котором каждое след. число отлич-ся от предыдущего только одним разрядом. Карта Карно может быть составлена для любого кол-ва переменных,однако удобно работать при кол-ве переменных не более пяти.Вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена можно приступать к минимизации. Если необх-мо получить мин.ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по след.правилам(на примере ДНФ):объединяем смежные клетки содержащие 1 в область,так чтобы одна область содержала 2n (n=0,1,2,…) клеток(помним про то что крайние строки и столбцы являются соседними между собой),в области не должно находится клеток содержащих нули;область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);не смежные области расположенные симметрично оси(ей) могут объединятся в одну;область должна быть как можно больше,а кол-во областей как можно меньше;области могут пересекаться; возможно несколько вариантов накрытия.Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных,если неменяющаяся переменная нулевая, проставляем над ней инверсию и т.д.для всех областей. Конъюнкции областей объединяем дизъюнкцией.

 

4)Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике-нормальная форма,в кот.булева формула имеет вид конъюнкции нескольких дизъюнктов.КНФ удобна для автоматического док-ва теорем.Любая булева формула может быть приведена к КНФ.Впрочем,при этом размер булевой формулы может возрасти экспоненциально.Так, например,2n дизъюнктов потребуется,чтобы записать след.формулу:

3)Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике-нормальная форма,в кот.булева формула имеет вид дизъюнкции нескольких конъюнктов.ДНФ удобна для автоматич. доказывания теорем.Любая булева формула может быть приведена к ДНФ.Впрочем,при этом размер булевой формулы может возрасти экспоненциально.Так,например,2n конъюнктов потребуется,чтобы записать след. формулу: