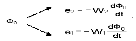Разветвляющий вычислительный процесс.

Разв.выч. процесс реализ-ся по одному из нескольких заранее предусмотренных направлений в зав-ти от вып-я нек.условия (логического выражения). //Ветвящийся процесс, включающий в себя две ветви, наз-тся простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.//Разв.выч. процесс, содержащий две ветви, схематично может быть изображен с помощью структуры выбора (структура разветвления), которая содержит три элемента: логическое условие, ветвь ДА и ветвь НЕТ. В любом конкретном случае процесс реализуется только по одной ветви, а выполнение остальных исключается.

Разв.выч.процесс реал-ся благодаря наличию команд условного перехода. JCC – усл.переход. Это набор команд, кажд. из кот-х вып-т переход, если удовлетв-ся соотв-ющее условие. Команды усл.перехода: JA – если выше, JNBE – если не ниже или равно, JAE – если выше или равно, JB – если ниже, JC – если перенос, JBE – если ниже или равно, JE – если равно, JZ – если 0, JG – если больше JGE – если больше или равно, JL – если меньше, JNG – если не больше, JNE – если не равно, JNZ – если не 0, JNO – если нет переполн-я, JO – если есть переполн-е, JPO – если нечетное, JP–если есть четность, JS–если есть знак, JNS-если нет знака.

 

 

Рекурсивный вычислительный процесс.

Рекурсия-процедура, вызывающая сама себя. Когда функция A в своем теле вызывает только одну рекурсивную функцию (саму себя), то это простая рекурсии. Косвенной рекурсия - это явление, когда рекурсивные функции вызывают друг друга (например, функция А вызывает B, а функция B вызывает A).

Прямая рекурсия	Косвенная рекурсия
void A(){ Операторы; A(); Операторы; }	void A(){ Операторы; B(); Операторы; } void B(){ Операторы; A(); Операторы; }

Рекурсивные алгоритмы сложнее отлаживать, но порой они позволяют очень гибко и красиво решить задачу. Любой рекурсивный алгоритм можно заменить нерекурсивным, но это будет дольше реализовать. Рекурсия часто применяется при решении задач с нисходящим динамическим программированием, а так же в переборных задачах. Рекурсивная функция не должна вызывать себя всегда, иначе программа работать не сможет. При реализации рекурсивных алгоритмов необходимо уделять внимание тому, чтобы алгоритм был конечным. Факториал. Самый простой пример рекурсивного решения - задача о вычислении факториала.. Здесь нужно определить некоторую функцию F(n), которая будет вычислять значение n! через саму себя. В данном случае воспользуемся рекуррентной ф-лой:F(n) = F(n-1)*n. условие выхода: если n<2, то ответ равен 1. Т.о., в тех случаях, когда n<2, функция не будет себя вызывать, что будет гарантировать выход из рекурсии.//Вычисление факториала int F(int n) // {if n<2 then return 1; // else return F(n-1)*n; // }

 

 

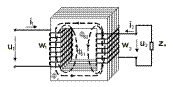
Трансформаторы.

Трансформатор представляет собой статическое электромагнитное устр-во, предназначенное для преобраз-я переменного тока одного напряж-я в переменный ток др.напряж-я той же частоты.//Чаще всего применяются однофазные и трехфазные трансформаторы.Трансформаторы с другим числом фаз исп-ся в спец.устр-вах. Простейший трансформатор (рис.) сост-т из магнитомягкого замкнутого магнитопровода (сердечника) и двух обмоток.

Рис. Простейший однофазный трансформатор (магнитопровод стержневого типа). //Магнитопровод служит для концентрации и прохождения магнитного потока. Он должен обладать минимальным сопротивлением магнитному потоку и выполняться из магнитомягкого ферромагнитного материала. //Принцип действия трансформатора основан на законе электромагнитной индукции. К первичной обмотке подключается переменное U₁, по ней потечет ток i₁, который создаст магнитодвижущую силу (мдс) i₁W₁. МДС в свою очередь создаст переменный магнитный поток, который, замыкаясь по магнитопроводу, будет наводить в обеих обмотках магнитодвижущую силу. В первичной обмотке возникает эдс самоиндукции, а во вторичной – эдс взаимной индукции. U₁→i₁→F₁=W₁i₁→ (Ф₀+Ф_б), где Ф0 – основной магнитный поток, пересекающий обе обмотки; Фб – поток рассеяния, пересекающий одну из обмоток.

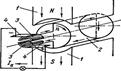
Машины постоянного тока.

Машина постоянного тока — электрическая машина для преобраз-я мех.энергии в эл. постоянного тока (генератор) или для обратного преобразования (двигатель). Каждая машина постоянного тока может работать как в режиме генератора, так и в режиме двигателя. Такое свойство присуще всем типам вращающихся электрических машин и называется обратимостью. Про двигатель. На рисунке обозначен индуктор 1. Вращающаяся часть машины состоит из укрепленных на валу цилиндрического якоря 2 и коллектора 3. Якорь состоит из сердечника, набранного из листов электротехнической стали, и обмотки, укрепленной на сердечнике якоря. Обмотка якоря в показанной на рисунке машине постоянного тока имеет один виток. Концы витка соединены с изолированными от вала медными пластинами коллектора, число которых в рассматриваемом случае равно двум. На коллектор налегают две неподвижные щетки 4, с помощью которых обмотка якоря соединяется с внешней цепью.

Если щетки подключить к источнику постоянного тока, то в витке будет протекать эл.ток и в рез-те взаимод-я тока с внешним магнитным полем возникнет электромагнитная сила и соответствующий вращающий момент М, виток придет во вращение. Коллектор обеспечивает эл.соед-е обмотки вращающегося якоря с неподвижными элементами внешней электрической цепи и синхронное изменение направления тока в элементах обмотки. В результате переключения проводников витка ток в каждом из них меняет свое направление каждые пол-оборота, т.е. коллектор преобразует постоянный ток во внешней цепи якоря в переменный ток обмотки якоря. Режим генератора. В генераторе коллектор явл-ся механическим выпрямителем, кот.преобразовывает переем.ток обмотки якоря в постоянный ток во внешней цепи.//Для перехода машины постоянного тока из режима генератора в режим двигателя и обратно при неизменной полярности полюсов и щеток и при неизменном направлении вращения требуется только изменение направления тока в обмотке якоря.