
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие существуют процедуры обучения искусственных нейронных сетейСодержание книги
Поиск на нашем сайте
Среди всех интересных свойств искусственных нейронных сетей ни одно не захватывает так воображения, как их способность к обучению. Их обучение до такой степени напоминает процесс интеллектуального развития человеческой личности что может показаться, что достигнуто глубокое понимание этого процесса. Но проявляя осторожность, следует сдерживать эйфорию. Возможности обучения искусственных нейронных сетей ограниченны, и нужно решить много сложных задач, чтобы определить, на правильном ли пути мы находимся. Тем не менее уже получены убедительные достижения, такие как "говорящая сеть" Сейновского, и возникает много других практических применений. Цель обучения. Сеть обучается, чтобы для некоторого множества входов давать желаемое (или, по крайней мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор. Алгоритмы обучения. Существует великое множество различных алгоритмов обучения, которые однако делятся на два больших класса: детерминистские и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором – она производится на основе действий, подчиняющихся некоторому случайному процессу. Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети - какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов. Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.
(Ниже приведена схема обучения с учителем.)
Несмотря на многочисленные прикладные достижения, обучение с учителем критиковалось за свою биологическую неправдоподобность. Трудно вообразить обучающий механизм в мозге, который бы сравнивал желаемые и действительные значения выходов, выполняя коррекцию с помощью обратной связи. Если допустить подобный механизм в мозге, то откуда тогда возникают желаемые выходы? Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью. (Ниже представлена схема обучения без учителя).
Большинство современных алгоритмов обучения выросло из концепций Хэбба. Им предложена модель обучения без учителя, в которой синаптическая сила (вес) возрастает, если активированны оба нейрона, источник и приемник. Таким образом, часто используемые пути в сети усиливаются и феномен привычки и обучения через повторение получает объяснение.
В искусственной нейронной сети, использующей обучение по Хэббу, наращивание весов определяется произведением уровней возбуждения передающего и принимающего нейронов. Это можно записать как wij(n+1) = w(n) + где wij(n) – значение веса от нейрона i к нейрону j до подстройки, wij(n+1) – значение веса от нейрона i к нейрону j после подстройки, Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению. Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования. Подробно о алгоритмах, правилах и других спецификах обучения будет написано дальше. Искусственные нейронные сети, подобно биологическим, являются вычислительной системой с огромным числом параллельно функционирующих простых процессоров с множеством связей. Несмотря на то, что при построении таких сетей обычно делается ряд допущений и значительных упрощений, отличающих их от биологических аналогов, искусственные нейронные сети демонстрируют удивительное число свойств, присущих мозгу, — это обучение на основе опыта, обобщение, извлечение существенных данных из избыточной информации [11]. Нейронные сети могут менять свое поведение в зависимости от состояния окружающей их среды. После анализа входных сигналов (возможно, вместе с требуемыми выходными сигналами) они самонастраиваются и обучаются, чтобы обеспечить правильную реакцию. Обученная сеть может быть устойчивой к некоторым отклонениям входных данных, что позволяет ей правильно «видеть» образ, содержащий различные помехи и искажения [1]. В 50-х годах прошлого века группа исследователей объединила биологические и физиологические подходы и создала первые искусственные нейронные сети. Тогда казалось, что ключ к искусственному интеллекту найден. Но, хотя эти сети эффективно решали некоторые задачи из области искусственного зрения — предсказания погоды и анализа данных, иллюзии вскоре рассеялись. Сети были не в состоянии решать другие задачи, внешне похожие на те, с которыми они успешно справлялись. С этого времени начался период интенсивного анализа. Были построены теории, доказан ряд теорем. Но уже тогда стало понятно, что без привлечения серьезной математики рассчитывать на значительные успехи не следует. С 70-х годов в научных журналах стали появляться публикации, касающиеся искусственных нейронных сетей. Постепенно был сформирован хороший теоретический фундамент, на основе которого сегодня создается большинство сетей. В последние два десятилетия разработанная теория стала активно применяться для решения прикладных задач. Появились и фирмы, занимающиеся разработкой прикладного программного обеспечения для конструирования искусственных нейронных сетей. К тому же 90-е годы ознаменовались приходом искусственных нейронных сетей в бизнес, где они показали свою реальную эффективность при решении многих задач — от предсказания спроса на продукцию до анализа платежеспособности клиентов банка.
Для того чтобы нейронная сеть могла решать эти задачи, ее необходимо обучить. Способность к обучению является основным свойством мозга. Для искусственных нейронных сетей под обучением понимается процесс настройки архитектуры сети (структуры связей между нейронами) и весов синаптических связей (влияющих на сигналы коэффициентов) для эффективного решения поставленной задачи. Обычно обучение нейронной сети осуществляется на некоторой выборке. По мере процесса обучения, который происходит по некоторому алгоритму, сеть должна все лучше и лучше (правильнее) реагировать на входные сигналы. Выделяют три парадигмы обучения: с учителем, самообучение (без учителя) и смешанная. В первом способе известны правильные ответы к каждому входному примеру, а веса подстраиваются так, чтобы минимизировать ошибку. Обучение без учителя позволяет распределить образцы по категориям за счет раскрытия внутренней структуры и природы данных. При смешанном обучении комбинируются два вышеизложенных подхода. Обучить нейронную сеть – значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы "А", мы спрашиваем его: "Какая это буква?" Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: "Это буква А". Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют "обучение с учителем".
Оказывается, что после многократного предъявления примеров веса нейронной сети стабилизируются, причем нейронная сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "нейронная сеть выучила все примеры", "нейронная сеть обучена", или "нейронная сеть натренирована". В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную нейронную сеть считают натренированной и готовой к применению на новых данных. Важно отметить, что вся информация, которую нейронная сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения нейронной сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать нейронную сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки нейронной сети требуется хотя бы несколько десятков (а лучше сотен) примеров. Обучение нейронных сетей – сложный и наукоемкий процесс. Алгоритмы обучения нейронных сетей имеют различные параметры и настройки, для управления которыми требуется понимание их влияния (см. рисунок 2).
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть – знать доступную для сети информацию. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети – какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов. Наиболее распространенные алгоритмы обучения нейронных сетей:
Пошаговый прямой или обратный отбор входных данных
Предпочтение следует отдавать тем алгоритмам, которые позволяют обучить нейронную сеть за небольшое число шагов и требуют мало дополнительных переменных. Это связано с тем, что обучение сетей производится на компьютерах с ограниченным объемом оперативной памяти и небольшой производительностью. Как правило, для обучения используются персональные компьютеры [13]. Стохастические алгоритмы требуют очень большого числа шагов обучения. Это делает невозможным их практическое использование для обучения нейронных сетей больших размерностей. Экспоненциальный рост сложности перебора с ростом размерности задачи в алгоритмах глобальной оптимизации также делает невозможным их использование для обучения нейронных сетей больших размерностей. Метод сопряженных градиентов очень чувствителен к точности вычислений, особенно при решении задач оптимизации большой размерности. Методы, учитывающие направление антиградиента на нескольких шагах алгоритма, и методы, включающие в себя вычисление матрицы Гессе, требуют дополнительных переменных [5]. Все используемые на данный момент алгоритмы обучения нейронных сетей базируются на оценочной функции, которой оценивается качество работы всей сети в целом. При этом имеется некоторый алгоритм, который в зависимости от полученного значения этой оценки каким-то образом подстраивает изменяемые параметры системы. Обычно эти алгоритмы характеризуются сравнительной простотой, однако не позволяют за приемлемое время получить хорошую систему управления или модель для достаточно сложных объектов. Именно здесь человек пока еще намного опережает в скорости настройки любую автоматику. Тем не менее, при разработке нейронных сетей можно выделить два основных этапа: · ·
Существует несколько методов уменьшения времени обучения многослойных нейронных сетей. Все они основаны на принципе достаточности, т.е. когда ошибка нейронной сети не превышает некоторого значения. В качестве таких методов предлагаются: изменение весовых коэффициентов нейронной сети, коррекция шага изменения весовых коэффициентов, реорганизация распознаваемых классов. Обучение нейронной сети происходит до тех пор, пока ее ошибка не станет близкой к нулю. Это, как правило, приводит к значительным тратам временных ресурсов, так как иногда может оказаться вполне достаточным, чтобы ошибка обучения нейронной сети не превышала некоторого значения, гораздо больше удаленного от нуля. Степень достаточности обучения нейронной сети во многом определяется исходя их условий конкретной задачи и желаемого результата. Предположим, дана некоторая задача классификации. Требуется решить ее, используя многослойную нейронную сеть, обучаемую с помощью алгоритма обратного распространения ошибки. Как правило, в процессе обучения нейронной сети для оценки погрешности обучения выделяют два вида ошибок: глобальные и локальные. Локальные ошибки содержат ошибки нейронов выходного слоя, а глобальные - ошибки всей нейронной сети на i-м обучающем наборе. Идеальным считается такое обучение, после которого нейронная сеть полностью повторяет обучающую выборку. Такое обучение является трудозатратным, а в некоторых случаях и просто невозможным. Это вызвано тем, что различные классы в обучающей выборке могут иметь схожие объекты, и чем их будет больше, тем сложнее предстоит процесс обучения нейронной сети. Суть принципа достаточности заключается в отказе от стремления к идеалу при поиске решения задачи. Если этот принцип перенести на процесс обучения нейронной сети, то можно сказать, что 100% точность распознавания требуется далеко не во всех случаях. Для того чтобы объект распознавания был правильно определен в свой класс вполне достаточно, чтобы ошибка нейронной сети на конкретном обучающем наборе не превосходила некоторого δ. Максимальное значение δ, при котором будет сохраняться заданная точность распознавания, зависит от характера обучающей выборки. В качестве параметров характеризующих обучающую выборку, рассмотрим ее полноту и противоречивость [18]. Полнота обучающей выборки характеризует обеспеченность классов обучающими наборами. Считается, что для каждого класса количество обучающих наборов должно хотя бы в 3-5 раз превосходить количество признаков класса, используемое в этих наборах. Для расчета полноты обучающей выборки можно воспользоваться следующей формулой:
Для того, чтобы определиться с условными обозначениями, приведем ниже следующую модель нейрона:
Функция активации (активационная функция, функция возбуждения) – функция, вычисляющая выходной сигнал искусственного нейрона. В качестве аргумента принимает сигнал
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.138 (0.011 с.) |



 OUTi OUTj,
OUTi OUTj,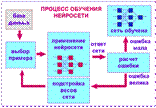

 где: nF – число классов, удовлетворяющих вышеописанному правилу;n – общее число классов.
где: nF – число классов, удовлетворяющих вышеописанному правилу;n – общее число классов. где: NA – количество противоречивых наборов;
где: NA – количество противоречивых наборов; 
 , получаемый на выходе входного сумматора
, получаемый на выходе входного сумматора  . Наиболее часто используются следующие функции активации.
. Наиболее часто используются следующие функции активации.


