
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютно непрерывные функции и неопределенный интеграл ЛебегаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Абсолютно непрерывные функции
Конечная на отрезке
Выполняется неравенство
Последнее неравенство, на самом деле, можно заменить на более сильное неравенство
Конечную систему интервалов можно заменить также на счетную систему интервалов. Множество абсолютно непрерывных функций обозначим Очевидно, что абсолютно непрерывная функция является непрерывной, но не наоборот. Простейшим примером абсолютно непрерывной функции является функция, удовлетворяющая условию Липшица
Отметим следующие свойства абсолютно непрерывных функций: 1. Если 2. Если 3. Если 4. Абсолютно непрерывная функция имеет почти всюду конечную производную. Если производная абсолютно непрерывной функции почти всюду равна нулю, она является константой. Говорят, что функция обладает своством 5. Абсолютно нерерывные функции облавдают свойством 6. Теорема Банаха – Зарецкого. Функция является абсолютно непрерывной тогда и только тогда, когда она имеет ограниченную вариацию и обладает свойством 7. Теорема Фихтенгольца. Пусть
2. Неопределенный интеграл Лебега
Если Из абсолютной непрерывности интеграла Лебега вытекает теорема. Теорема 1. Неопределенный интеграл является абсолютно непрерывной функцией. Из этой теоремы и свойств абсолютно непрерывных функций неопределенный интеграл имеет конечную производную почти всюду. Но в этом можно утверждать большее. Теорема 2. Производная неопределенного интеграла Из этой теоремы в качестве следствия получаем, что абсолютно непрерывная функция является неопределенным интегралом своей производной. В каких точках существует производная неопределенного интеграла? Точка
Нетрудно убедиться, что каждая точка непрерывности является точкой Лебега.
Теорема 3. Неопределенный интеграл Теорема 3 доказывается легко. Более сложным является утверждение. Теорема 4. Если Для неопределенного интеграла легко подсчитать ее полную вариацию. Теорема 5. Если
3. Разложение функций ограниченной вариации
Ранее мы показали, что функция Теорема 6. Если
где
Восстановление первообразной функции
Пусть непрерывная функция
в котором интеграл понимается по Риману. Но производная, даже ограниченная, может быть не интегрируемой по Риману. Оказывается, что в случае ограниченности производной функцию можно восстановить по формуле (1) с помощью интеграла Лебега. Справедливо даже более сильное утверждение. Теорема 7. Если для функции Но производная функции может существовать всюду и не быть интегрируемой по Лебегу. Таким образом, интеграл Лебега не полностью решает задачу восстановления первообразной функции по ее производной. Это делает интеграл Перрона – Данжуа.
Библиографический список
1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа: учеб. пособие. – 7-е изд. – М.: Физматлит, 2004. – 572с.
2. Действительный анализ в задачах: учеб. пособие для вузов / П.Л. Ульянов [и др.] – М.: Физматлит, 2005. – 416с. 3. Золотухин А.Я. Элементы теории множеств, меры и интеграла Лебега: учеб. пособие. – Тула: ТулГУ, 2007. – 107с. 4. Методические указания к практическим занятиям по дисциплине «Действительный анализ». Тула: ТулГУ, 2013. — (Электронное издание). 5. Методические указания к самостоятельной работе студента по дисциплине «Действи000тельный анализ». Тула: ТулГУ, 2013. — (Электронное издание).
|
||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.132.221 (0.011 с.) |

 функция
функция 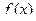 называется абсолютно непрерывной, если для любого
называется абсолютно непрерывной, если для любого  существует такое
существует такое  , что для любой конечной системы не пересекающихся интервалов
, что для любой конечной системы не пересекающихся интервалов  , для которой
, для которой


 .
.
 , то
, то  Если
Если  не обращается в нуль, то
не обращается в нуль, то 
 , а
, а  удовлетворяет условию Липшица, то
удовлетворяет условию Липшица, то  .
.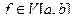 .
. , если она множество меры нуль переводит в множество меры нуль. Только такие функции измеримые множества переводят в измеримые множества.
, если она множество меры нуль переводит в множество меры нуль. Только такие функции измеримые множества переводят в измеримые множества. . Тогда
. Тогда 

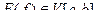
 , то функция
, то функция  называется неопределенным интегралом функции
называется неопределенным интегралом функции  .
.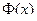 почти всюду равна подынтегральной функции
почти всюду равна подынтегральной функции  называется точкой Лебега функции
называется точкой Лебега функции 
 функции
функции 
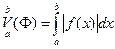 , то есть полное изменение абсолютно непрерывной функции равно интегралу от модуля ее производной.
, то есть полное изменение абсолютно непрерывной функции равно интегралу от модуля ее производной. и непрерывной функции
и непрерывной функции  ограниченной вариации:
ограниченной вариации:  Функция
Функция  Положим
Положим  . Она является абсолютно непрервной и для непрерывной функции
. Она является абсолютно непрервной и для непрерывной функции 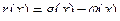 почти всюду
почти всюду  . Такую функцию мы ранее назвали сингулярной. Итак, для функции ограниченной вариации мы установили следующее разложение, называемое разложением Лебега.
. Такую функцию мы ранее назвали сингулярной. Итак, для функции ограниченной вариации мы установили следующее разложение, называемое разложением Лебега.
 - абсолютно непрерывная функция,
- абсолютно непрерывная функция,  - сингулярная функция. Если функция
- сингулярная функция. Если функция  - также неубывающие.
- также неубывающие. на отрезке
на отрезке  всюду имеет производную
всюду имеет производную  . Как по производной
. Как по производной  , то
, то , (1)
, (1)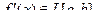 , то для нее справедливо равенство (1), в которм интеграл понимается по Лебегу.
, то для нее справедливо равенство (1), в которм интеграл понимается по Лебегу.


