
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции ограниченной вариации. Их свойства
1. Определение функции ограниченной вариации
Пусть Величину Не всякая непрерывная функция будет функцией ограниченной вариации. Такой функцией является, например, следующая функция:
С другой стороны, функция ограниченной вариации не обязана быть непрерывной. Мы увидим, что любая монотонная функция является функцией ограниченной вариации и она может иметь счетное число точек разрыва первого рода.
2. Свойства функций ограниченной вариации
Отметим следующие свойства функций ограниченной вариации: 1. Функция ограниченной вариации ограничена. Действительно, для любого
2. Монотонная функция является функцией ограниченной вариации. Действительно, для любого разбиения
Поэтому 3. Если Действительно, если
4. Если
5. Функция является функцией ограниченной вариации тогда и только тогда, когда она представляется в виде разности двух неубывающих функций. Достаточность вытекает из свойств 2,3. Для доказательства необходимости рассмотрим функцию
По свойству 4 она неубывает. Покажем, что функция
Следствие. Функция ограниченной вариации имеет не более чем счетное число точек разрыва.
3. Принцип выбора Хелли
В приложениях важна теорема Хелли, называемая принципом Хелли. Сначала приведем две леммы. Лемма 1. Пусть на отрезке Лемма 1 доказывается с помощью теоремы Больцано-Вейерштрасса и диагонального процесса Кантора. Лемма 2. Пусть на отрезке При доказательстве леммы 2 применяется лемма 1 для множества рациональных точек на отрезке
Теорема Хелли. Пусть на отрезке
Тогда из семейства
4. Непрерывные функции ограниченной вариации
Для непрерывных функций ограниченной вариации свойство 5 можно уточнить: 1. Если 2. Если Наряду с величиной Очевидно, что 3. Если
ЛЕКЦИЯ 15 Интеграл Римана - Стилтьеса
1. Определение интеграла Римана - Стилтьеса
Пусть на отрезке
Число
не зависящий от разметки, то есть если для любого Множество пар функций
2. Свойства интеграла Римана – Стилтьеса
Отметим свойства интеграла, вытекающие из его определения: 1. 2. 3. 4. Для любого
если интеграл слева существует. 5. Из существования одного из интегралов
Последнее равенство называется формулой интегрирования по частям. 6. Если
7. Если
8. Если
3. Предельный переход для интеграла Римана – Стилтьеса
Для предельного перехода под знаком интеграла Римана – Стилтьеса приведем две теоремы. Теорема 1. Пусть
Теорема 2. Пусть
ЛЕКЦИЯ 16
|
|||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.230.44 (0.013 с.) |
 - конечная функция,
- конечная функция,  - разбиение отрезка
- разбиение отрезка  ,
,  .
. назовем полным изменением функции
назовем полным изменением функции  на отрезке
на отрезке 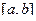 . Если
. Если  , то функцию
, то функцию  назовем функцией ограниченной вариации. Множество всех таких функций обозначим
назовем функцией ограниченной вариации. Множество всех таких функций обозначим 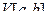 .
.





 , то
, то  Если к тому же
Если к тому же  , то
, то 
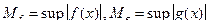 , то
, то ,
, 
 ,
, 
 , то для любого
, то для любого 


 также неубывает. Если
также неубывает. Если  , то по свойству 4
, то по свойству 4
 . Для любого счетного множества
. Для любого счетного множества  из семейства
из семейства  можно выделить последовательность функций, сходящуюся в каждой точке
можно выделить последовательность функций, сходящуюся в каждой точке 
 задано бесконечное равномерно ограниченное семейство неубывающих функций
задано бесконечное равномерно ограниченное семейство неубывающих функций  . Тогда из семейства
. Тогда из семейства  можно выделить последовательность функций, сходящуюся в каждой точке отрезка
можно выделить последовательность функций, сходящуюся в каждой точке отрезка  , причем для некоторого
, причем для некоторого  и всех функций этого семейства выполнены неравенства
и всех функций этого семейства выполнены неравенства
 .
. , то функция
, то функция  .
.
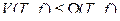 . Тем не менее, справедливо утверждение.
. Тем не менее, справедливо утверждение. , то
, то
 и
и  ,
, 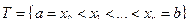 - разбиение отрезка
- разбиение отрезка  осуществляют разметку разбиения
осуществляют разметку разбиения  - мелкость или диаметр разбиения. Составим сумму
- мелкость или диаметр разбиения. Составим сумму
 называется интегралом Римана - Стилтьеса на отрезке
называется интегралом Римана - Стилтьеса на отрезке  (пишут
(пишут  ), если существует
), если существует
 существует
существует  такое, что для любого разбиения
такое, что для любого разбиения  и любой его разметки выполняется неравенство:
и любой его разметки выполняется неравенство: 
 , для которых существует интеграл Римана – Стилтьеса, обозначим
, для которых существует интеграл Римана – Стилтьеса, обозначим 

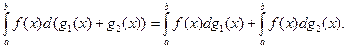


 вытекает существование другого интеграла и равенство
вытекает существование другого интеграла и равенство
 ,
, 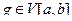 , то
, то  и справедлива оценка
и справедлива оценка
 и существует в каждой точке
и существует в каждой точке  , то
, то .
. ,
,  ,
,  ,
, 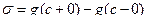 , то
, то
 ,
,  и
и  на
на  . Тогда
. Тогда
 ,
,  ,
,  на
на  . Тогда
. Тогда  и
и



