
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение интегралов Римана и Лебега
1. Интеграл Летега сильнее интеграла Римана
Напомним построение интеграла Римана. Пусть функция
то определим две
Имеем
верхняя и нижняя суммы Дарбу. Известно, что для интегрируемой по Риману функции
Пусть Теорема 10.1. Если функция
Доказательство. Возьмем последовательность разбиений
Нетрудно убедиться, что
поэтому существуют измеримые функции
Для них
поэтому для неотрицательной функции
Так как
Теорема доказана. Для функции Дирихле
2. Критерий Лебега существования интеграла Римана
Теорема 10.2 (А.Лебег). Пусть функция Доказательство. Необходимость. Пусть Покажем, что
и при некотором
Тогда для любого
что доказывает непрерывность Достаточность. По условию
получаем
то существует единственное число, разделяющее верхние и нижние суммы Дарбу для функции Отметим, что Интегрируемая по Риману функция может иметь несчетное множество точек разрыва. Пусть
Если
Покажем, что каждая точка из Несобственный интеграл Римана и интеграл Лебега несравнимы. Однако для положительных функций интеграл Лебега сильнее несобственного интеграла Римана.
ЛЕКЦИЯ 14
|
|||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.125.171 (0.01 с.) |
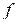 ограничена на
ограничена на  . Если имеется разбиение
. Если имеется разбиение


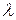 -простые функции
-простые функции .
.
 ее интеграл
ее интеграл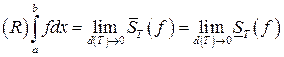 . (10.1)
. (10.1) — множество всех
— множество всех  — интеграл Лебега.
— интеграл Лебега. , то
, то  и
и .
. отрезка
отрезка  такую, что
такую, что  (
( ) и
) и  являются измельчением
являются измельчением  (
( ). Пусть
). Пусть .
.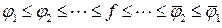 ,
, .
. . По теореме Лебега 9.3
. По теореме Лебега 9.3 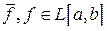 и (10.1)
и (10.1)

 .
.

 и
и .
.

 , но
, но  .
. ограничена на
ограничена на  — множество точек разрыва
— множество точек разрыва  — множество таких
— множество таких  для которых не выполняется хотя бы одно из равенств
для которых не выполняется хотя бы одно из равенств  ,
,  . В теореме 10.1 было показано, что
. В теореме 10.1 было показано, что  . Если разбиение
. Если разбиение  , то пусть
, то пусть  . Очевидно, что
. Очевидно, что  .
. . Пусть
. Пусть  ,
,  . Найдутся
. Найдутся  такие, что
такие, что

 .
.
 ,
, .
. , где
, где  . Возьмем произвольное
. Возьмем произвольное 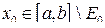 и
и  , то в некоторой окрестности
, то в некоторой окрестности 
 . Выберем последовательность разбиений отрезка
. Выберем последовательность разбиений отрезка 
 с
с  (
( ),
),  и
и  , для которых
, для которых  . В таком случае
. В таком случае  . Ввиду произвольности
. Ввиду произвольности  и условия
и условия ,
, ; причем это выполнено для всех
; причем это выполнено для всех  . Следовательно,
. Следовательно, 


 .
. — канторово множество на
— канторово множество на  ,
,  и
и
 , то в силу открытости
, то в силу открытости  найдется окрестность
найдется окрестность  . Следовательно,
. Следовательно,  и непрерывна в
и непрерывна в  . Таким образом, все точки
. Таким образом, все точки  . Так как
. Так как  , то по теореме 10.2
, то по теореме 10.2  .
.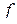 . Действительно, если
. Действительно, если  , то
, то  . Но в любой окрестности
. Но в любой окрестности  . Остается вспомнить, что
. Остается вспомнить, что 


