
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продолжение меры. Мера Бореля. Пополнение меры. Мера Лебега
1. Продолжение меры
Пусть Можно ли меру на полукольце расширить на более широкий класс множеств, замкнутый относительно некоторых операций? Единственно ли это продолжение, если оно существует? Ответы на эти вопросы дает следующая теорема, которая приводится без доказательства. Теорема 3.1. Пусть
Теорема 3.2. Если мера
Доказательство. По теореме 3.1
поэтому для любого
Выберем
Так как
то
и
Отсюда, из свойства 3) и монотонности меры (3.1)
Теорема доказана.
2. Мера Бореля
Семейство полуинтервалов в 3. Пополнение меры
Определение. Мера Отметим, что по свойству монотонности меры Мера Бореля, к сожалению, не является полной. Это можно доказать следующим образом. Алгебра Теорема 3.3. Пусть Доказательство. Так как всякое
Так как
Ввиду свойства 3) меры,
Покажем независимость
Используя монотонность и свойство 3) меры, получаем
Аналогично
Взяв попарно непересекающиеся множества
Это доказывает счетную аддитивность Рассмотрим другую меру
следует, что Если Мера
4. Мера Лебега
По теореме 3.3 меру Бореля Итак, Задачи. Вычислить меру Лебега следующих множеств: 1) 2) 3) 4) Решения. 1) Так как
2) Так как
3) Всякое открытое множество
4) Канторово множество
Значит,
Канторово множество имеет мощность континуума и меру нуль. В троичном разложении точек канторова множества будут участвовать только цифры 0 и 2. ЛЕКЦИЯ 7
|
||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.78 (0.022 с.) |
 ,
,  — меры, определенные соответственно на
— меры, определенные соответственно на  и
и  . Меру
. Меру  называют продолжением
называют продолжением  и
и  для любого
для любого  . Согласно данного определения продолжение
. Согласно данного определения продолжение 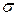 -конечной меры является
-конечной меры является  -конечной мерой.
-конечной мерой. —
—  -конечная мера на полукольце
-конечная мера на полукольце  . Существует единственное продолжение
. Существует единственное продолжение  до меры
до меры 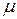 на
на  , при этом для всякого
, при этом для всякого 
 .
. является продолжением меры на кольце
является продолжением меры на кольце  , то для любых
, то для любых  ,
,  ,
,  существует
существует  такое, что
такое, что .
. ,
, такие, что ряд
такие, что ряд  сходится и
сходится и . (3.1)
. (3.1)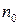 так, чтобы
так, чтобы 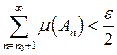 и положим
и положим .
. .
.
 .
.
 образует полукольцо
образует полукольцо  , на котором определена мера
, на котором определена мера 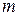 (длина), так что
(длина), так что  . Мера
. Мера 
 до меры
до меры 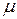 на
на  . Эта мера на
. Эта мера на  -алгебре борелевских множеств
-алгебре борелевских множеств  называется мерой Бореля.
называется мерой Бореля. -алгебре
-алгебре  , называется полной, если условия
, называется полной, если условия  ,
,  и
и 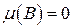 влекут
влекут  .
. .
. имеет мощность континуума. Канторово множество, которое будет построено позже, замкнуто, имеет меру Бореля нуль и мощность континуума. Множество его подмножеств имеет мощность гиперконтинуума и, значит, среди них есть не борелевское множество. Однако, не полную меру можно пополнить.
имеет мощность континуума. Канторово множество, которое будет построено позже, замкнуто, имеет меру Бореля нуль и мощность континуума. Множество его подмножеств имеет мощность гиперконтинуума и, значит, среди них есть не борелевское множество. Однако, не полную меру можно пополнить.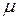 — мера на
— мера на  (где
(где  ,
,  — подмножество какого-либо множества
— подмножество какого-либо множества  с
с  , содержащую
, содержащую  на
на  .
. может быть записано в виде
может быть записано в виде  , то
, то  . Проверим, что
. Проверим, что  (
( ,
,  с
с  ),
),  . Имеем
. Имеем .
. , а множество, стоящее во второй скобке, содержится в
, а множество, стоящее во второй скобке, содержится в 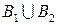 и
и  , то
, то  . Пусть
. Пусть 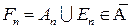 , где
, где  ,
,  с
с  (
(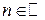 ). Тогда
). Тогда .
. . Следовательно,
. Следовательно,  . Установлено, что
. Установлено, что  имеет два представления
имеет два представления .
. .
. , что доказывает равенство
, что доказывает равенство .
.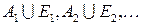 из
из  и
и  . Тогда
. Тогда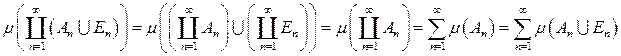
 ,
,  , то
, то  .
. на
на  . Для произвольного
. Для произвольного  (
( с
с  .
. . Это доказывает единственность продолжения
. Это доказывает единственность продолжения  (
( с
с  ) и
) и  , то
, то  и
и  , где
, где  , а
, а  с
с  (так как
(так как  ). Это означает, что
). Это означает, что  и, следовательно,
и, следовательно,  – полная мера. Теорема доказана.
– полная мера. Теорема доказана. на
на  . Условимся меру
. Условимся меру  и называть мерой Лебега на
и называть мерой Лебега на  и называть множества из
и называть множества из  измеримыми по Лебегу множествами в
измеримыми по Лебегу множествами в  , где
, где  — борелевское,
— борелевское,  ,
,  ,
,  .
. ;
; ;
; — открытое в
— открытое в  — канторово множество.
— канторово множество. , то по свойству непрерывности меры Лебега сверху
, то по свойству непрерывности меры Лебега сверху .
. ,
,  , то
, то .
. на прямой является объединением конечного или счетного числа попарно непересекающихся интервалов
на прямой является объединением конечного или счетного числа попарно непересекающихся интервалов  , называемых составляющими. Тогда
, называемых составляющими. Тогда .
. является замкнутым множество, потому
является замкнутым множество, потому 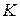 — борелевское и, значит, измеримо по Лебегу. Множество
— борелевское и, значит, измеримо по Лебегу. Множество  является открытым. Рассмотрим его составляющие интервалы, получающиеся при построении
является открытым. Рассмотрим его составляющие интервалы, получающиеся при построении  интервал
интервал  , (называемый интервалом первого ранга). На втором этапе каждый из оставшихся двух отрезков
, (называемый интервалом первого ранга). На втором этапе каждый из оставшихся двух отрезков  и
и  делится на три равных отрезка и удаляется (в каждом из этих двух отрезков) средний интервал. Интервалы, удаляемые на втором этапе (их два, а длина каждого
делится на три равных отрезка и удаляется (в каждом из этих двух отрезков) средний интервал. Интервалы, удаляемые на втором этапе (их два, а длина каждого  ), называем интервалами второго ранга и их объединение обозначаем через
), называем интервалами второго ранга и их объединение обозначаем через  . Каждый из интервалов
. Каждый из интервалов  -го ранга (т.е. удаляемые на
-го ранга (т.е. удаляемые на  -ом этапе) имеет длину их число
-ом этапе) имеет длину их число  , а их объединение обозначаем через
, а их объединение обозначаем через  . Тогда
. Тогда  ,
,  — попарно непересекающиеся множества и, следовательно,
— попарно непересекающиеся множества и, следовательно, .
. .
.


