
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мощность множества. Мощность основных классов функцийСтр 1 из 10Следующая ⇒
Иванов В.И. профессор, д.ф.-м.н.
КОНСПЕКТ ЛЕКЦИЙ по дисциплине
Действительный анализ
Направление подготовки: 02.03.01 «Математика и компьютерные науки» Профиль подготовки: «Математическое и компьютерное моделирование»
Форма обучения: очная
Тула 2018 г. Рассмотрено на заседании кафедры протокол № 8 от 22 мая 2018 г.
Зав. кафедрой________________В.И. Иванов
СОДЕРЖАНИЕ ЛЕКЦИЯ 1. Операции над множествами. 4 ЛЕКЦИЯ 2. Мощность множества. Мощность основных классов функций. 6 ЛЕКЦИЯ 3. Множества в евклидовых пространствах. Множества типа ЛЕКЦИЯ 4. Системы множеств. Полукольцо, кольцо, алгебра, ЛЕКЦИЯ 5. Функции множества на полукольце. Меры. Свойства меры. 14 ЛЕКЦИЯ 6. Продолжение меры. Мера Бореля. Пополнение меры. Мера Лебега. 18 ЛЕКЦИЯ 7. Свойства меры Лебега. Приближение измеримых по Лебегу множеств открытыми и замкнутыми множествами. Единственность меры Лебега на прямой. 22 ЛЕКЦИЯ 8. Определение измеримых функций. Операции над измеримыми функциями. Последовательности измеримых функций. Приближение измеримых функций простыми. 25 ЛЕКЦИЯ 9. Пространство с мерой. Теорема Д.Ф. Егорова. Сходимость почти всюду и по мере. Теорема Рисса. ЛЕКЦИЯ 10. Интеграл Лебега для простых функций. Интеграл Лебега для произвольных функций. Интегрируемость измеримых ограниченных функций. 34 ЛЕКЦИЯ 11. Традиционные свойства интеграла Лебега. Абсолютная непрерывность интеграла Лебега. Неравенство Чебышева. 38 ЛЕКЦИЯ 12. Предельные теоремы для интеграла Лебега. Теорема Беппо-Леви о монотонной сходимости. Лемма Фату. Теорема Лебега об ограниченной сходимости. 42 ЛЕКЦИЯ 13. Сравнение интегралов Римана и Лебега 45 ЛЕКЦИЯ 14. Функции ограниченной вариации. Их свойства. 48 ЛЕКЦИЯ 15. Интеграл Римана-Стилтьеса. 50 ЛЕКЦИЯ 16. Теорема Лебега о производной монотонной функции. Ее интегрируемость по Лебегу. 52 ЛЕКЦИЯ 17. Абсолютно непрерывные функции и неопределенный интеграл Лебега 54
ЛЕКЦИЯ 1 Операции над множествами 1. Основные операции над множествами
Множество
Отметим следующие операции над множествами: 1) 2) 3) 4) 5) 6) Справедливы два важных равенства, называемых формулами де Моргана. Пусть
2. Последовательности множеств. Верхний и нижний пределы
Пусть Последовательность множеств называется возрастающей, если
Последовательность множеств называется убывающей, если
Отметим следующие простые утверждения: 1. Если последовательность множеств
2. Если множества 3. Если Верхним пределом последовательности множеств
Нетрудно убедиться, что верхний предел последовательности множеств – это множество всех элементов, которые принадлежат бесконечно многим Нижним пределом последовательности множеств
Нижний предел последовательности множеств – это множество всех элементов, которые принадлежат всем Если
то последовательность множеств
Пример. Пусть последовательность множеств имеет вид
Найти для нее верхний и нижний пределы. Решение. Так как для любого
Так как для любого
Когда последовательность является сходящейся. Как и в случае числовых последовательностей можно указать два достаточных условия: 1. Если последовательность множеств
2. Если последовательность множеств
ЛЕКЦИЯ 2 ЛЕКЦИЯ 3 Множества в евклидовых пространствах. Множества типа
1.
Пусть С помощью покоординатного сложения и покоординатного умножения на число можно определить в
Оно удовлетворяет всем аксиомам скалярного произведения: 1. 2. 3. 4. Скалярное произведение позволяет определить длину вектора
Оно удовлетворяет всем свойствам нормы: 1. 2. 3. Скалярное произведение позволяет определить расстояние между векторами
Оно удовлетворяет всем свойствам метрики: 1. 2. 3. Скалярное произведение позволяет определить угол между векторами
и, в частности, ортогональность двух векторов: Корректность определения угла между векторами и доказательство неравенства треугольника для нормы и метрики вытекают из неравнства Коши - Буняковского:
2. Предельные точки
Открытым шаром Последовательность Точка Теорема 3. Точка Множество, лежащее в некотором шаре, называется ограниченным. Теорема 4 (Больцано – Вейерштрасса). Всякое бесконечное ограниченное множество имеет по крайней мере одну предельную точку.
3. Замкнутые и открытые множества
Множество, каждая точка которого лежит в нем с некоторой окрестностью называется открытым. Множество, содержащее все предельные точки, называется замкнутым. Операция присоединения к множеству его предельных точек называется замыканием. Замыкание множества является замкнутым (наименьшим замкнутым, содержащим множество) множеством. Отметим свойства открытых и замкнутых множеств: 1a. Все 2a. Объединение любого числа окрытых множеств открыто. 3a. Пересечение конечного числа открытых множеств открыто. 1b. Все 2b. Пересечени любого числа замкнутых множеств замкнуто. 3b. Объединение конечного числа замкнутых множеств замкнуто. Двойственные свойства открытых и замкнтых множеств вытекают из следующего соотношения между ними. Лемма 1. Множество Лемма 2. Пусть
Доказательство. Пусть
4. Стуктура открытых множеств
Известна структура открытого множества на прямой. Теорема 5. Любое открытое множество на прямой является объединением не более чем счетного числа непересекающихся открытых интервалов. При Теорема 6. Любое открытоемножество Доказательство. Для Пусть
То есть
5. Множества типа
Множество, являющееся объединением счетного числа замкнутых множеств, называется множеством типа Задача 1. Доказать, что множество рациональных чисел на отрезке Функцией, непрерывной на множестве иррациональных чисел и разрывной на множестве рациональных чисел является известная функция Римана. Задача 2. Доказать, что множество иррациональных чисел на отрезке Отсюда будет вытекать, что не существует ограниченной функции на отрезке, для которой множеством точек разрыва является множество иррациональных чисел.
ЛЕКЦИЯ 4 Системы множеств. Полукольцо, кольцо, алгебра, Борелевские множества 1. История возникновения интеграла Лебега
Интеграл, известный как интеграл Лебега, был введен французским математиком Анри Лебегом, в 1902 г. для функций, определенных на отрезке прямой. Насколько сильна была потребность в интеграле, расширяющем известные к тому времени интегралы, и в то же время насколько удачным оказалось определение Лебега показывает то, что уже в десятилетие, последовавшее за этим, новый интеграл завоевал всеобщее признание, а для многих математиков разных стран — стал объектом интенсивного исследования. Они подвергли его всестороннему исследованию: изучались свойства интеграла, предлагались эквивалентные определения, устанавливались многообразные приложения. Из этих математиков назовем лишь нескольких: У.Г. Юнг, Ф. Рисс, Б.Леви, Дж. Витали, Д.Ф.Егоров, Н.Н.Лузин, М.Фреше, П.Фату и, конечно, А.Лебег.
В 1910 г. Лебегом же было предложено определение интеграла от функции, заданной в В результате было введено и распространилось понятие интеграла, ставшее вскоре главным орудием исследования самых разнообразных вопросов математики и математического естествознания. Современная теория дифференциальных уравнений, математическая и теоретическая физика, теория линейных операторов, теория вероятностей и статистика, а также другие разделы математики используют в качестве теоретической основы и важнейшего инструмента теорию меры и интеграла Лебега. Эти понятия — мера и интеграл Лебега — составляют фундамент метрической теории функций действительного переменного. Изучению интеграла Лебега будет предшествовать изучение теории меры и теории измеримых функций.
2. Системы множеств. Полукольцо, кольцо, алгебра,
Пусть Определение. Непустое семейство 1) для любых 2) для любых
Пусть
Нетрудно убедиться, что Определение. Непустая система 1) 2) Система подмножеств 3) Алгебра называется 4) Отметим следующие простые свойства кольца и алгебры: а) Если
Действительно,
б) Всякое кольцо является полукольцом. Действительно, условие 1 следует из свойства а). Если в) Всякое полукольцо содержит пустое множество. Действительно, если г) Если Действительно, если
3. Кольца и алгебры, порожденные системами множеств
Определение. Если
Теорема 1.1. Для любой непустой системы Доказательство. Приведем для Теорема 1.2. Пусть Доказательство. Пусть 1) Если
2) Если 3) Если
где 4) Покажем, что
Теперь достаточно воспользоваться этапами 1-3. 5) Наконец,
Теорема доказана.
4. Борелевские множества
Определение. Если Примерами борелевских множеств являются замкнутые множества, множества Теорема 1.3. Справедливо равенство
Доказательство. Пустое множество является борелевским в Установим обратное включение. Рассмотрим произвольный интервал
Известно, что всякое открытое множества
поэтому Теорема доказана.
ЛЕКЦИЯ 5 ЛЕКЦИЯ 6 ЛЕКЦИЯ 7 ЛЕКЦИЯ 8 ЛЕКЦИЯ 9 Пространство с мерой. Теорема Д.Ф. Егорова. Сходимость почти всюду и по мере. Теорема Рисса. 1. Пространство с мерой
Определение. Тройка Будем предполагать, что Говорят, что некоторое свойство выполняется Определение. Функции Отметим, что эквивалентные функции измеримы одновременно. Если
2. Теорема Д.Ф. Егорова
Теорема 6.1. Пусть Доказательство. Пусть
Каждое из множеств
и, ввиду сходимости
Для всякого
Положим
и
Докажем равномерную сходимость
Это доказывает равномерную сходимость на последовательности функций
3. Сходимость почти всюду и по мере. Теорема Рисса
Определение. Последовательность
Теорема 6.2. Если Доказательство. Положим для
Для всех
следовательно,
Переходя к пределу при
так как
|
|||||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.189.48 (0.201 с.) |
 и
и 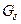 8
8 -алгебра. Борелевские множества. 11
-алгебра. Борелевские множества. 11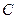 -свойство измеримой функции Н.Н. Лузина. 29
-свойство измеримой функции Н.Н. Лузина. 29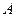 задается указанием элементов, из которых оно состоит. Пишут
задается указанием элементов, из которых оно состоит. Пишут 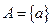 ,
,  . Пустое множество обозначается
. Пустое множество обозначается  . Оно является подмножеством любого множества.
. Оно является подмножеством любого множества. - вложение множеств (
- вложение множеств (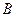 ). Оно означает, что если
). Оно означает, что если  . Если
. Если  , то
, то 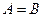 . Верно и обратное утверждение.
. Верно и обратное утверждение.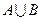 - объединение двух множеств, которое состоит из всех элементов, входящих по крайней мере в одно из множеств
- объединение двух множеств, которое состоит из всех элементов, входящих по крайней мере в одно из множеств 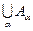 .
.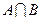 - персечение двух множеств, которое состоит из всех элементов, входящих и в
- персечение двух множеств, которое состоит из всех элементов, входящих и в  . Два множества, имеющие пустое пересечение называются не пересекающимися или дизъюнктными.
. Два множества, имеющие пустое пересечение называются не пересекающимися или дизъюнктными. - разность двух множеств, которое состоит из всех элементов
- разность двух множеств, которое состоит из всех элементов  - симметрическая разность двух множеств.
- симметрическая разность двух множеств. - декартово произведение двух множеств. Аналогично можно определить декартово произведение конечного или счетного числа множеств. Их элементами будут векторы или последовательности.
- декартово произведение двух множеств. Аналогично можно определить декартово произведение конечного или счетного числа множеств. Их элементами будут векторы или последовательности.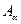 - произвольные пдмножества
- произвольные пдмножества 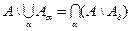 ,
,  .
. - последовательность множеств.
- последовательность множеств.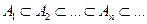
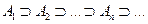
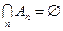 , то
, то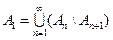 .
. попарно дизъюнктны и
попарно дизъюнктны и  , то последовательность
, то последовательность 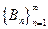 убывает и
убывает и 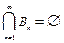 .
. , то
, то  , причем множества
, причем множества 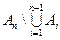 попарно дизъюнктны.
попарно дизъюнктны.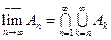 .
.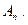
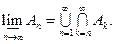 .
.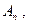 начиная с некоторого номера, причем этот номер может зависеть от элемента.
начиная с некоторого номера, причем этот номер может зависеть от элемента.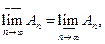
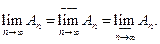
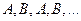
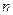
 , то
, то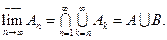
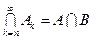 , то
, то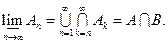
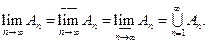

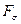 и
и 
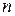 -мерное евклидово пространство
-мерное евклидово пространство -
-  операции сложения векторов и умножения на действительные числа. С этими двумя операциями
операции сложения векторов и умножения на действительные числа. С этими двумя операциями 

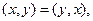
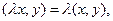

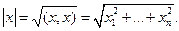

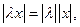
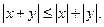
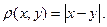
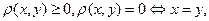




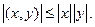
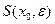 с центром в точке
с центром в точке  и радиусом
и радиусом  называется совокупность точек
называется совокупность точек  , для которых
, для которых  . Всякий окрытый шар с центром в
. Всякий окрытый шар с центром в 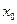 называют окрестностью этой точки. Окрестность радиуса
называют окрестностью этой точки. Окрестность радиуса 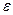 называют
называют 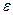 -окрестностью.
-окрестностью. называется сходящейся к
называется сходящейся к 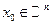 (
(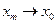 ), если для любого
), если для любого 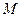
 для всех
для всех 
 , если в любой окрестности
, если в любой окрестности  , отличная от
, отличная от 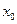 .
. , отличных от
, отличных от  -открытое тогда и только тогда, когда его дополнение множество
-открытое тогда и только тогда, когда его дополнение множество  - замкнутое. В
- замкнутое. В и
и 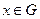 . Тогда среди всех шаров с центром в
. Тогда среди всех шаров с центром в 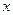 , содержащися в
, содержащися в  - множество радиусов шаров с центром в
- множество радиусов шаров с центром в 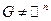 , то
, то 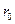 - точная верхняя грань
- точная верхняя грань 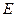 . Тогда
. Тогда 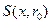 - искомый шар.
- искомый шар. ввиду отсутствия отношения порядка в
ввиду отсутствия отношения порядка в 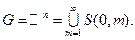 Пусть
Пусть 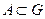 -множество точек с рациональными координатами,
-множество точек с рациональными координатами, 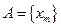 . Для
. Для 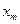 по лемме 2 существует открытый шар
по лемме 2 существует открытый шар 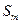 наибольшего радиуса с центром в
наибольшего радиуса с центром в 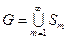 . Для этого достаточно доказать включение
. Для этого достаточно доказать включение 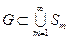 .
.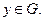 Тогда для некоторого
Тогда для некоторого 
 . Подберем такую рациональную точку
. Подберем такую рациональную точку 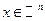 , что
, что 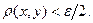 Тогда
Тогда  ,
, 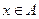 ,
, 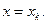 Далее,
Далее, 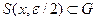 . Действительно, если
. Действительно, если 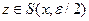 , то
, то
 . Из включения
. Из включения 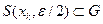 следует, что шар
следует, что шар 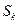 имеет радиус, не меньший чем
имеет радиус, не меньший чем 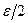 . Поэтому
. Поэтому 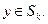 Теорема доказана.
Теорема доказана.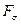 и
и 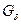
 . Множество, являющееся пересечением счетного числа открытых множеств, называется множеством типа
. Множество, являющееся пересечением счетного числа открытых множеств, называется множеством типа 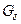 . Множества этих типов естественно появляются в теории функций. Например, в математическом анализе доказывается, что множество точек разрыва ограниченной функции на отрезке имеет тип
. Множества этих типов естественно появляются в теории функций. Например, в математическом анализе доказывается, что множество точек разрыва ограниченной функции на отрезке имеет тип 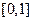 имеет тип
имеет тип  и не имеет тип
и не имеет тип  -алгебра.
-алгебра.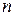 -мерном евклидовом пространстве, а в 1915 году М. Фреше распространил интегрирование на функции, заданные на произвольном множестве с мерой. Это последнее определение интеграла (на произвольном множестве с мерой) в математической литературе называют интегралом Лебега, или абстрактным интегралом Лебега.
-мерном евклидовом пространстве, а в 1915 году М. Фреше распространил интегрирование на функции, заданные на произвольном множестве с мерой. Это последнее определение интеграла (на произвольном множестве с мерой) в математической литературе называют интегралом Лебега, или абстрактным интегралом Лебега. — произвольное непустое множество.
— произвольное непустое множество. подмножеств множества
подмножеств множества 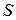 называют полукольцом, если
называют полукольцом, если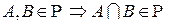 ,
, ,
, 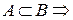 найдется такое конечное семейство множеств
найдется такое конечное семейство множеств 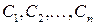 из
из 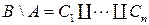 .
.
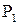 и
и  являются полукольцами.
являются полукольцами.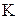 подмножеств какого-либо множества называется кольцом, если выполнены следующие требования:
подмножеств какого-либо множества называется кольцом, если выполнены следующие требования: ,
, .
.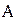 множества
множества  — кольцо, для которого выполнено условие
— кольцо, для которого выполнено условие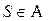 .
.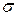 -алгеброй, если
-алгеброй, если .
.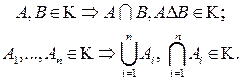
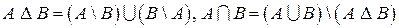 .
. ,
,  , то
, то  .
.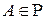 , то
, то  ,
,  только в случае
только в случае 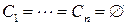 .
.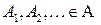 , то
, то  .
.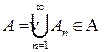 и
и 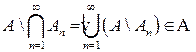 . Отсюда
. Отсюда 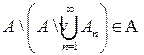 .
.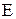 — какое-либо семейство подмножеств
— какое-либо семейство подмножеств  ) кольцо (
) кольцо (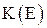 (
( ).
).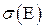 .
.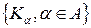 — семейство всех колец подмножеств
— семейство всех колец подмножеств 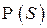 — множество всех подмножеств
— множество всех подмножеств 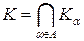 — искомое кольцо, порожденное
— искомое кольцо, порожденное 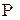 — полукольцо множеств. Тогда
— полукольцо множеств. Тогда  есть совокупность всех множеств вида
есть совокупность всех множеств вида  , где
, где 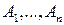 — попарно непересекающиеся множества из
— попарно непересекающиеся множества из 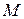 — семейство всех конечных объединений попарно непересекающихся множеств из
— семейство всех конечных объединений попарно непересекающихся множеств из 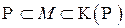 , и достаточно показать, что
, и достаточно показать, что  , где
, где 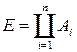 ,
, 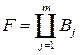 . Проверку, что
. Проверку, что  — кольцо осуществим в несколько этапов.
— кольцо осуществим в несколько этапов. . Но
. Но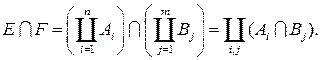
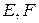 — непересекающиеся, то
— непересекающиеся, то  . Это очевидно, ибо
. Это очевидно, ибо 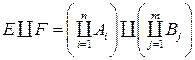 .
.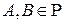 , то
, то  . Действительно, в этом случае
. Действительно, в этом случае 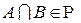 и
и  . Тогда
. Тогда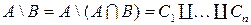 ,
,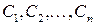 из
из 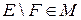 . Действительно,
. Действительно, .
.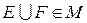 , так как
, так как .
.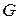 — система открытых множеств на прямой
— система открытых множеств на прямой  , то
, то 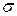 -алгебру
-алгебру 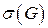 обозначают
обозначают  и множества из
и множества из 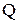 и
и  .
.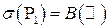 .
.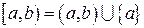 . Тогда
. Тогда  . Значит,
. Значит, 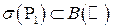 .
.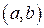 и пусть
и пусть 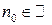 такое, что
такое, что 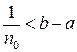 . Тогда
. Тогда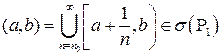
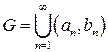 ,
,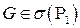 . Так как
. Так как 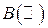 — наименьшая (по включению)
— наименьшая (по включению)  .
. -свойство измеримой функции Н.Н. Лузина.
-свойство измеримой функции Н.Н. Лузина.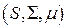 называется пространством с мерой, если
называется пространством с мерой, если  — измеримое пространство,
— измеримое пространство, 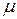 — мера на
— мера на 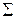 .
.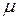 — полная
— полная 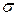 -конечная мера.
-конечная мера.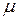 -почти всюду (
-почти всюду (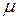 -п.в. или просто п.в.), если оно выполняется на множестве
-п.в. или просто п.в.), если оно выполняется на множестве 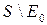 , где
, где 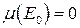 .
. называются
называются 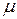 -эквивалентными (
-эквивалентными (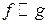 ), если
), если 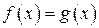
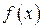 измерима и
измерима и 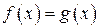 для
для 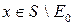 ,
, 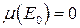 , то
, то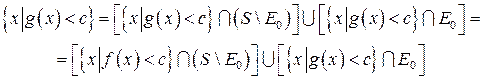
 -измеримо.
-измеримо. — пространство с конечной полной мерой и
— пространство с конечной полной мерой и 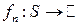 — последовательность измеримых функций сходящаяся
— последовательность измеримых функций сходящаяся 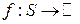 . Тогда функция
. Тогда функция 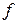 измерима и для всякого
измерима и для всякого 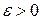 существует такое измеримое множество
существует такое измеримое множество  , что
, что 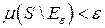 и на
и на 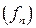 сходится равномерно к
сходится равномерно к 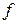 .
. таково, что
таково, что 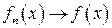 ,
, 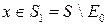 . Функция
. Функция 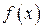 измерима на
измерима на  и на
и на 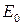 , следовательно,
, следовательно, 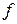 измерима. Пусть для
измерима. Пусть для 
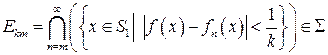 . (6.1)
. (6.1)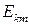 измеримо при любом
измеримо при любом 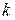

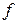 на
на  ,
, 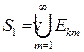 ,
,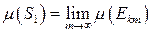 .
.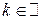 найдется
найдется  такое, что
такое, что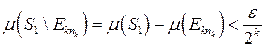 .
. . Имеем
. Имеем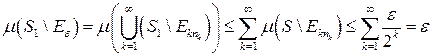 ,
, .
. на
на 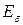 . Взяв произвольное
. Взяв произвольное  , найдем
, найдем 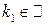 так, что
так, что 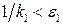 . Так как
. Так как 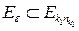 , то из (6.1) следует, что для
, то из (6.1) следует, что для  и
и 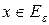
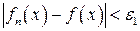 .
.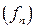 к
к  по
по 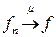 ), если любого
), если любого 
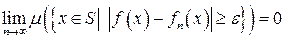 .
.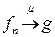 , то
, то 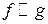 .
.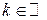
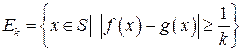 .
.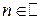
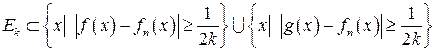 ,
, .
.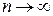 , получим
, получим  ,
, 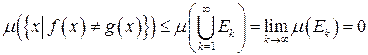 ,
,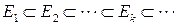 .
.


