
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближение измеримых функций простыми
1. Определение измеримых функций
Пусть Определение. Функция
Если Определение. Пусть
Отметим, что Непрерывная функция Теорема 5.1. Доказательство. Так как множество Пусть теперь
Следовательно,
значит,
2. Операции над измеримыми функциями
Так как для
а для
то из измеримости функции Так как для
то из измеримости функции Теорема 5.2. Если функции Доказательство. Пусть
Каждое из множеств Заметим, что измеримой будет и функция Следствие. Если функции
Доказательство. Измеримость
Далее
3. Последовательности измеримых функций
Теорема 5.3. Если Доказательство. Имеем
Пусть для
Отсюда будет следовать измеримость Если Обратно, если
4. Приближение измеримых функций простыми
Определение. Функция
Простая функция измерима; сумма и произведение простых функций также является простой функцией. Теорема 5.4. Пусть функция
Доказательство. Для
Если
Значит, Если
Это доказывает, что Следствие 5.1. Пусть функция Доказательство. Пусть
Тогда
Последовательность простых функций
Следствие 5.2. Если функция Доказательство. Пусть
Тогда, очевидно, что для
ЛЕКЦИЯ 9 Пространство с мерой. Теорема Д.Ф. Егорова. Сходимость почти всюду и по мере. Теорема Рисса. 1. Пространство с мерой
Определение. Тройка Будем предполагать, что Говорят, что некоторое свойство выполняется Определение. Функции Отметим, что эквивалентные функции измеримы одновременно. Если
2. Теорема Д.Ф. Егорова
Теорема 6.1. Пусть
Доказательство. Пусть
Каждое из множеств
и, ввиду сходимости
Для всякого
Положим
и
Докажем равномерную сходимость
Это доказывает равномерную сходимость на последовательности функций
3. Сходимость почти всюду и по мере. Теорема Рисса
Определение. Последовательность
Теорема 6.2. Если Доказательство. Положим для
Для всех
следовательно,
Переходя к пределу при
так как Теорема 6.3. Если Доказательство. Пусть
поэтому
Теорема доказана. Обратное утверждение неверно. Для примера возьмем меру Лебега
Вместе с тем, какую бы точку Теорема 6.4. Если Доказательство. Вследствие
и последовательность измеримых множеств
Положим
то, вследствие непрерывности меры,
Если
Это доказывает, что
4.
Теорема 6.5. Пусть Доказательство. Напомним, что для Пусть
Положим
Сужение
Покажем, что
Очевидно, включение
Установим обратное включение. Имеем
поэтому
что вместе с (6.3) дает (6.2). Если
Тогда учитывая (6.2), получим
Так как множество По следствию 4.2 существует такое замкнутое в
Следствие 6.1. Пусть функция
Если при этом Доказательство. Пусть
Если
ЛЕКЦИЯ 10
|
||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.104.109 (0.1 с.) |
 — произвольное множество,
— произвольное множество,  —
—  -алгебра его подмножеств. Пару
-алгебра его подмножеств. Пару  называют измеримым пространством, а множества из
называют измеримым пространством, а множества из  — измеримыми.
— измеримыми. называется
называется  -измеримой (или просто измеримой), если для любого
-измеримой (или просто измеримой), если для любого 
 .
. и
и  , то измеримую функцию называют измеримой по Лебегу, а если
, то измеримую функцию называют измеримой по Лебегу, а если  и
и  , то измеримую функцию называют измеримой по Борелю или борелевской функцией.
, то измеримую функцию называют измеримой по Борелю или борелевской функцией. ,
,  —
—  -алгебра подмножеств множества
-алгебра подмножеств множества  . Функция
. Функция  называется измеримой на
называется измеримой на  , если для любого
, если для любого 
 .
. .
. является борелевской, так как прообраз открытого множества открыт. Всякая борелевская функция измерима и по Лебегу.
является борелевской, так как прообраз открытого множества открыт. Всякая борелевская функция измерима и по Лебегу.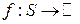
 .
. , то достаточность очевидна.
, то достаточность очевидна.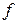 — измеримая функция. Обозначим через
— измеримая функция. Обозначим через  семейство всех таких подмножеств
семейство всех таких подмножеств  в
в  , для которых
, для которых  . По условию для любого
. По условию для любого 
 . Если
. Если  , то
, то  и
и .
. . Если
. Если  , то
, то  и
и ,
, . Следовательно
. Следовательно  есть
есть 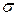 -алгебра (
-алгебра ( ), содержащая множества
), содержащая множества  . Так как
. Так как  наименьшая
наименьшая  -алгебра, содержащая множества
-алгебра, содержащая множества  , то
, то  . Теорема доказана.
. Теорема доказана.
 ,
,
 ,
, .
.
 ,
, следует измеримость функции
следует измеримость функции  .
. измеримы, то функция
измеримы, то функция  также измерима.
также измерима. в
в 
 .
. ,
,  измеримо, следовательно, измеримо и их пересечение. Остается заметить, что множество пар
измеримо, следовательно, измеримо и их пересечение. Остается заметить, что множество пар  счетно. Теорема доказана.
счетно. Теорема доказана. .
. и
и  измеримы, то измеримы будут и функции
измеримы, то измеримы будут и функции .
. следует из равенства
следует из равенства .
.
 (
( ) — последовательность
) — последовательность  -измеримых функций, то функции
-измеримых функций, то функции  ,
,  ,
, 
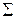 -измеримы.
-измеримы.

 . Покажем, что
. Покажем, что . (5.1)
. (5.1)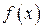 .
. , то существует такое
, то существует такое 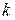 , что
, что  . Для этого
. Для этого  можно найти
можно найти  такое, что для
такое, что для  будет выполнимо неравенство
будет выполнимо неравенство  . Значит,
. Значит,  войдет в правую часть (5.1).
войдет в правую часть (5.1). принадлежит правой части (5.1), то существуют
принадлежит правой части (5.1), то существуют  такие, что для всех
такие, что для всех 
 . Значит,
. Значит,  . Теорема доказана.
. Теорема доказана. , определенная на измеримом пространстве
, определенная на измеримом пространстве  , называется простой, если для
, называется простой, если для 
 .
. измерима. Тогда существует неубывающая последовательность
измерима. Тогда существует неубывающая последовательность  неотрицательных простых функций, для которой
неотрицательных простых функций, для которой .
. и
и  положим
положим
 , то
, то  , а функция
, а функция  в этой же точке
в этой же точке  .
. . Если
. Если  , то
, то  , a
, a  принимает одно из двух значений
принимает одно из двух значений  ,
,  . В этом случае также
. В этом случае также 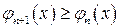 .
. , то существует
, то существует  такое, что
такое, что  и для любого
и для любого 
 .
. .
. измерима. Тогда существует последовательность простых функций
измерима. Тогда существует последовательность простых функций 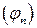 сходящаяся к
сходящаяся к  , для которой
, для которой  .
. .
. ,
,  — измеримые неотрицательные функции и
— измеримые неотрицательные функции и  . Согласно теореме 5.4, существуют две неубывающие последовательности неотрицательных простых функций
. Согласно теореме 5.4, существуют две неубывающие последовательности неотрицательных простых функций  и
и  , сходящихся к
, сходящихся к  .
. сходится к
сходится к  и
и .
. измерима и ограничена, то существует последовательность простых функций, равномерно сходящихся к
измерима и ограничена, то существует последовательность простых функций, равномерно сходящихся к 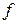 .
. такое, что
такое, что  . Для каждых
. Для каждых  и
и  положим
положим .
. ,
, .
. -свойство измеримой функции Н.Н. Лузина.
-свойство измеримой функции Н.Н. Лузина.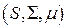 называется пространством с мерой, если
называется пространством с мерой, если  — измеримое пространство,
— измеримое пространство, 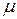 — мера на
— мера на 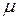 — полная
— полная 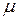 -почти всюду (
-почти всюду (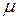 -п.в. или просто п.в.), если оно выполняется на множестве
-п.в. или просто п.в.), если оно выполняется на множестве 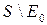 , где
, где 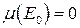 .
. называются
называются 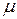 -эквивалентными (
-эквивалентными (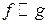 ), если
), если 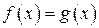
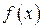 измерима и
измерима и 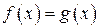 для
для 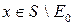 ,
, 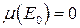 , то
, то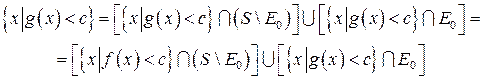
 -измеримо.
-измеримо. — пространство с конечной полной мерой и
— пространство с конечной полной мерой и 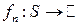 — последовательность измеримых функций сходящаяся
— последовательность измеримых функций сходящаяся 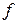 измерима и для всякого
измерима и для всякого 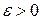 существует такое измеримое множество
существует такое измеримое множество  , что
, что 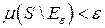 и на
и на 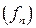 сходится равномерно к
сходится равномерно к  таково, что
таково, что 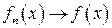 ,
, 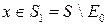 . Функция
. Функция  и на
и на 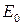 , следовательно,
, следовательно, 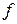 измерима. Пусть для
измерима. Пусть для 
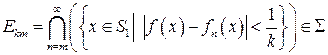 . (6.1)
. (6.1)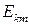 измеримо при любом
измеримо при любом 
 ,
, 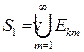 ,
,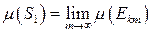 .
.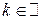 найдется
найдется  такое, что
такое, что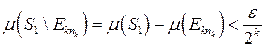 .
. . Имеем
. Имеем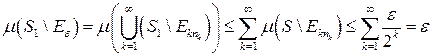 ,
, .
. на
на 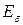 . Взяв произвольное
. Взяв произвольное  , найдем
, найдем 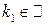 так, что
так, что 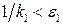 . Так как
. Так как 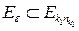 , то из (6.1) следует, что для
, то из (6.1) следует, что для  и
и 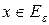
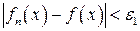 .
.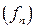 к
к  по
по 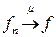 ), если любого
), если любого 
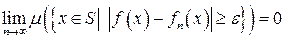 .
.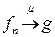 , то
, то 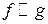 .
.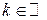
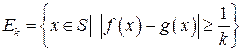 .
.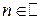
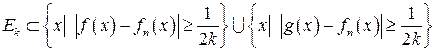 ,
, .
.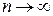 , получим
, получим  ,
, 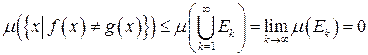 ,
,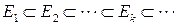 .
.
 , то
, то  .
. ,
,  . По теореме 6.1 существует множество
. По теореме 6.1 существует множество  ,
,  , на котором
, на котором  сходится к
сходится к  равномерно. Отсюда
равномерно. Отсюда  такое, что для всех
такое, что для всех 
 ,
,
 на
на  . Построим последовательность функций
. Построим последовательность функций  следующим образом:
следующим образом: 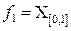 ,
,  , и для
, и для  (
( )
)  . Последовательность
. Последовательность  сходится по мере
сходится по мере  к функции
к функции 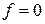 , так как для
, так как для  .
. не взять, найдется бесконечное множество номеров
не взять, найдется бесконечное множество номеров  , для которых
, для которых  при любом
при любом  . Это означает, что
. Это означает, что  не сходится к
не сходится к  ни для одного
ни для одного  . Тем не менее, справедлива следующая теорема.
. Тем не менее, справедлива следующая теорема. , то существует подпоследовательность
, то существует подпоследовательность 


 таких, что
таких, что .
. ,
,  . Так как
. Так как  — убывающая последовательность множеств и
— убывающая последовательность множеств и ,
, .
. ,
,  , то
, то  . Значит, найдется
. Значит, найдется  такое, что
такое, что  . Тогда
. Тогда  для всех
для всех  . Выберем
. Выберем  и
и  . Для всех
. Для всех 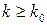
 .
. ,
,  , т.е.
, т.е.  -свойство измеримой функции Н.Н. Лузина
-свойство измеримой функции Н.Н. Лузина и функция
и функция 
 , что
, что  и сужение
и сужение  непрерывно (как функция на
непрерывно (как функция на  ).
). функция
функция  непрерывна на
непрерывна на  , если для любого открытого в
, если для любого открытого в  множества
множества  существует такое открытое в
существует такое открытое в  , что
, что  .
. ,
,  — семейство интервалов в
— семейство интервалов в  по теореме 4.1 найдется такое открытое и в
по теореме 4.1 найдется такое открытое и в  , что
, что .
. .
. обозначим через
обозначим через  . Имеем
. Имеем
 . (6.2)
. (6.2) . (6.3)
. (6.3)
 ,
, — произвольное открытое множество в
— произвольное открытое множество в  .
.
 открыто, то
открыто, то  .
. , что
, что  . На
. На  функция
функция  непрерывна и
непрерывна и .
. . Тогда для всякого
. Тогда для всякого  , такая что
, такая что .
. ,
,  , то
, то  ,
,  .
. , что
, что  и сужение
и сужение  непрерывно. Обозначим это сужение
непрерывно. Обозначим это сужение  и значениями
и значениями  на
на  и
и  на
на  . Тогда
. Тогда  , следовательно,
, следовательно, .
. ,
,  , то по построению
, то по построению  ,
,  .
.


