
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции множества на полукольце. Меры. Свойства меры
1. Функции множества
Функцией множества назовем функцию, определенную на каком-либо семействе множеств. Пусть а) неотрицательной, если для любого б) аддитивной, если для любых непересекающихся множеств
в) счетно аддитивной, если для любой последовательности попарно непересекающихся множеств
2. Меры
Наиболее важной функцией множества является мера. Определение. Мерой называют неотрицательную счетно-аддитивную функцию, определенную на полукольце (принимающую, возможно, значение Если Отметим, что мера пустого множества равна нулю, так как
Отсюда вытекает аддитивность меры:
Примеры мер. 1) Вначале установим счетную аддитивность
Следовательно, ряд с неотрицательными членами Теперь покажем, что
Поэтому
и Из равенства и условия ( 2) Аналогично проверяется, что если на полукольце
то 3) Пусть
характеристическая функция множества
Тогда
3. Свойства меры
Пусть 1) Если
Доказательство следует из равенства 2) (Монотонность меры). Если Доказательство следует из свойства 1. 3) Если
Доказательство. Пусть
4) Если Доказательство. Согласно счетной аддитивности и монотонности меры
5) (Непрерывность снизу). Если
Доказательство. Если
Тогда
6) (Непрерывность сверху). Пусть
В частности, если Доказательство. Пусть
Отсюда Если
ЛЕКЦИЯ 6
|
|||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.240.178 (0.014 с.) |
 - некоторое семейство множеств. Функция множества
- некоторое семейство множеств. Функция множества  называется:
называется:

 , для которых
, для которых  , будет
, будет
 , для которых
, для которых  , будет
, будет .
. ), не равную тождественно
), не равную тождественно  .
.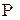 — полукольцо подмножеств
— полукольцо подмножеств  и
и 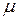 — мера на
— мера на  называют конечной, если
называют конечной, если  и
и  и
и 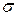 -конечной, если
-конечной, если  , где
, где 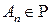 и
и  .
. .
. .
. и на полукольце
и на полукольце  определим следующую функцию
определим следующую функцию  . Покажем, что
. Покажем, что  —
—  — попарно непересекающиеся множества из
— попарно непересекающиеся множества из  , то есть для некоторых
, то есть для некоторых 
 . Тогда для произвольного
. Тогда для произвольного  из свойств длины имеем: "
из свойств длины имеем: " .
. сходится и его сумма не превосходит
сходится и его сумма не превосходит  .
. . Для этого возьмем произвольное
. Для этого возьмем произвольное  и пусть
и пусть  ,
,  (
( ). Тогда
). Тогда  — компактное множество и
— компактное множество и  . Ввиду компактности
. Ввиду компактности  такое, что
такое, что  . Из неравенства длина
. Из неравенства длина  длина
длина  выводим
выводим ,
, . Итак,
. Итак, .
. .
. .
. подмножеств
подмножеств  определим функцию
определим функцию  так, что
так, что
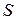 — произвольное (непустое) множество,
— произвольное (непустое) множество,
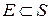 ,
,  — произвольное счетное множество в
— произвольное счетное множество в  — последовательность неотрицательных чисел. Для
— последовательность неотрицательных чисел. Для 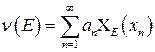 .
. — мера на
— мера на 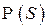 . Определенная таким образом мера
. Определенная таким образом мера  — мера, определенная на некоторой
— мера, определенная на некоторой  подмножеств
подмножеств  . Отметим ее свойства.
. Отметим ее свойства. ,
,  и
и  , то
, то .
. и аддитивности меры.
и аддитивности меры. , то
, то 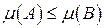 .
. — конечное или счетное семейство множеств из
— конечное или счетное семейство множеств из  таково, что
таково, что  , то
, то  и, в частности,
и, в частности, .
. ;
;  — семейство попарно непересекающихся множеств из
— семейство попарно непересекающихся множеств из  . Если
. Если  , то
, то  . Ввиду счетной аддитивности и монотонности
. Ввиду счетной аддитивности и монотонности 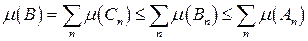 .
. , то
, то  .
. .
. — возрастающая последовательность множеств, то есть
— возрастающая последовательность множеств, то есть  из
из  .
. , то множества
, то множества  (
( ) попарно непересекающиеся и
) попарно непересекающиеся и .
.
 — убывающая последовательность множеств, то есть
— убывающая последовательность множеств, то есть 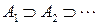 из
из  имеет конечную меру. Тогда
имеет конечную меру. Тогда
 , то
, то  .
. . Тогда для
. Тогда для 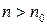
 . Последовательность множеств
. Последовательность множеств  (
( ) — возрастающая, следовательно,
) — возрастающая, следовательно,
 . Для окончания доказательства стоит только заметить, что
. Для окончания доказательства стоит только заметить, что  .
. при любом
при любом  , то свойство 6 может не выполняться, например, для
, то свойство 6 может не выполняться, например, для  ,
,  , а
, а 


